与传统磁流变液阻尼器相比，多孔泡沫金属磁流变液阻尼器的动态响应时间与其内部的磁流变液流动机理有着密切的关系。磁流变液在泡沫金属磁流变液阻尼器内部的流动示意图如图10.16 所示。线圈中没有通入电流时，在重力和毛细管力的作用下，磁流变液储存在泡沫金属中，如图10.16（a）所示；如图10.16（b）所示，接通电流后，磁场力克服重力和毛细管力，磁流变液被抽出至剪切间隙；当外加电流增加到一定值，剪切间隙内部磁场强度增加到一定强度后，被抽出的磁流变液达到活塞高度并随活塞一起作剪切运动，产生磁流变液效应，从而阻尼力发生变化，如图10.16（c）所示。
图10.16 泡沫金属磁流变液阻尼器内部磁流变液流动特性分析
当其他条件相同时，多孔泡沫金属磁流变液阻尼器阻尼力主要取决于从泡沫金属中被抽出的磁流变液的体积，被抽出的磁流变液的体积越大，磁流变液效应越强，阻尼力越大。而产生磁流变液效应的磁流变液体积的大小与从泡沫金属中抽出的磁流变液的上升高度相关，为此，本文通过建立磁流变液的上升高度模型描述磁流变液的动态响应时间。同时，该模型也反映了阻尼力的变化。
为建立多孔泡沫金属磁流变液阻尼器的响应时间模型，利用泡沫金属的管束模型，首先对微孔中磁流变液流动的表面张力进行计算，进而对泡沫金属中的磁流变液在外加磁场作用下进行受力分析，再根据牛顿第二定律得到运动方程，从而得到上升高度与时间的关系。
在磁流变液从泡沫金属中被抽出至剪切间隙并产生阻尼力这一过程中，磁流变液受到的作用力主要有：①磁场力Fm=μ0M ∇H；②磁流变液的重力G=mg=ρVg；③磁流变液所受到的表面张力F=σK（h）Sp；④范德华力及其他分子之间的作用力。
针对抽出至剪切间隙的磁流变液，根据牛顿第二定律得到其运动方程：
式中 V——磁流变液的上升体积；
ρ——磁流变液密度；
V——磁流变液的上升速度；
H——磁场强度；
M——磁化强度；
Sp——泡沫金属单孔面积；
g——重力加速度；
h——磁流变液的上升高度；
σ——表面张力；
K（h）——上升的磁流变液曲率。
磁流变液的动态运动特性不仅与外加磁场相关，而且磁流变液的上升表面形貌也对其上升过程有较大影响。
图10.17 磁流变液的上升简化模型
假设在外加磁场作用下，被抽出的磁流变液呈椭圆状，且在上升过程中，椭圆短半轴保持不变，如图10.17 所示，从而有：
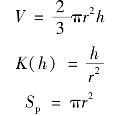
式中 r——多孔泡沫金属单孔的半径；
h——磁流变液的上升高度。
则有：
(www.xing528.com)
化简为：
假设：
此时，方程简化为：
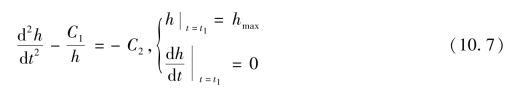
该方程组的物理意义为，在t=t1 时刻，磁流变液上升到最高点hmax，此时，在最高点处的速度为0。于是，问题转化为对磁流变液上升至最高点时刻t1 及最高点hmax的确定，即阻尼力达到最大稳定值的时刻。
分析该微分方程可知，若施加恒定磁场，磁流变液中的磁感应强度为一恒定值，此时，C1和C2 变为常数。
假设磁流变液的磁化强度M 正比于外加磁场强度H，磁流变液中B，H，M 三个矢量相互平行，则有
从而
式中 B，H，M——分别为磁流变液中的磁感应强度、磁场强度和磁化强度；
在等温条件下，磁流变液的磁化强度和磁导率与温度无关，于是有
则有
式中 χ——磁化率；
B（r）——被抽出的磁流变液中的磁感应强度。
带入相关参数，得到边界条件：
式（10.13）表明，外部条件一定时，磁流变液的上升高度主要取决于外部磁感应强度。将实验和仿真得到的磁感应强度与外加电流的关系带入式（10.13），利用mathmatic 求解，结合式（10.13）即可得到磁流变液的上升高度随时间变化的过程。以泡沫金属铜为例，得到磁流变液的上升高度随时间变化的曲线如图10.18 所示。
图10.18 磁流变液的上升高度与时间的关系
由图10.18 可知，没有外加磁场时，由于表面张力及其他作用力，磁流变液在泡沫金属中上升至一初始高度h0；线圈中通入电流后，磁场力克服重力及其他作用力，磁流变液开始下降，直到力达到平衡，此时，磁流变液回归零点；继续增加磁场强度，从泡沫金属中抽出至剪切间隙的磁流变液体积越来越大，磁流变液的上升高度也随之变大，直至上升到一高度后，磁场力与重力、表面张力及其他作用力达到平衡，此时，磁流变液加速度为零，上升至最高点；随后，由于阻碍磁流变液的上升作用力大于磁场力，磁流变液最终回到原点，但由于磁流变液在泡沫金属中可能产生回流，磁流变液流回到泡沫金属中，因此产生负方向的高度。
因此，磁流变液从泡沫金属中被抽出的上升高度不仅与外加磁场强度的大小有关，还与磁流变液的特性和泡沫金属的结构参数有关。总之，当施加的磁场力大于表面张力、粘滞阻尼力和重力的合外力时，磁流变液将从泡沫金属中抽出；反之，磁流变液将重新流回到泡沫金属中。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
