磁流变液中磁性颗粒成链的原因

磁流变液中的磁性颗粒在磁场作用下成链或链束的原因存在很多假说，常见的有磁畴理论、相变理论和场致偶极矩理论，本节从磁性粒子受力的角度分析了磁流变液中磁性颗粒成链的原因，为进一步研究磁流变液的上升现象提供了理论基础。

研究中作如下假设：①磁流变液中基液为非导磁性材料；②磁流变液中的铁磁性颗粒为圆球状，大小一致；③磁性颗粒充分磁化；④在微观状态下分析单个直链或者粒子受力时，不考虑单个链的倾斜。

假设磁流变液中的磁性颗粒的半径为R，由磁性物理学可知，颗粒被磁化后的磁矩为

式中　V——单个颗粒的体积；

　　　M——磁化强度；

　　　χm——磁性颗粒的磁化率；

　　　H——磁场强度。

式（5.1）中，单个粒子磁矩的方向和外磁场的方向一致。

颗粒j 在颗粒i 处产生的磁感应强度为

式中　μ0——真空磁导率；

　　　rij——两颗粒i 和j 之间相对位置的矢量。

如图5.1 所示，颗粒i 受到的磁场作用力为

式中　B——外加磁场的磁感应强度；

　　　mir和mjr——分别为磁矩mi 和mj 沿rij方向的分量；

　　　θij——rij与磁感应强度B 的夹角。

磁化颗粒的这种运动趋势与其受到的磁力特性有关，按磁偶极子理论，磁化颗粒即磁偶极子受到的磁力方向并不沿两颗粒的中心连线方向，而是与之呈一定角度，相对位置不同，角度也会不同，这也引起了两颗粒聚集或分离，其位置示意如图5.1 所示。

图5.1　磁流变液中磁性颗粒的受力(www.xing528.com)

（a）磁性颗粒的受力；（b）矢量方向示意图

若磁场为竖直方向，两粒子的位置如图5.1（b）所示，则两粒子之间的磁场力F 沿水平方向的分力Fmx和竖直方向的分力Fmz可由式（5.3）得到

若要颗粒聚合在一起形成链状结构，它们必须相互靠近，即Fmx和Fmz都为引力，也就是在式（5.4）中，两者的值均为正。

由sin θij（1 -5 cos2θij）=0，有

由（3 -5 cos2θij）cos θij=0，有

下面分3 种情况分析颗粒的运动。

(1)0 ≤θij ＜arccos

如图5.2（a）所示，两者水平和竖直方向的磁场力分量都为引力，磁性颗粒在两个方向上都相互靠拢，且在运动过程中夹角θij越来越小，最终颗粒沿磁场方向排列。

(2)arccos

如图5.2（b）所示，Fmx为引力，Fmz为斥力，磁性颗粒在水平方向靠拢，但在竖直方向远离，这样的运动使得夹角θij越来越小，达到一定程度后，Fmx也为引力，因此转化为第一种情况，最后颗粒聚合成链。

(3)arccos

如图5.2（c）所示，Fmx和Fmz都为斥力，颗粒相互远离。一般情况下，它们会分别与其他颗粒在远处形成链，这种情况避免了所有颗粒都聚在一起形成单一链的问题。

图5.2　颗粒在不同位置的运动情况

（a）0 ≤θij ＜arccos（/5）；（b）arccos（/5）≤θij ＜arccos（/5）；（c）arccos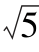（/5）≤θij≤π/2

由于影响磁流变液中颗粒成链的因素很多，比如磁性颗粒的大小分布及磁流变液的密度不均匀等，这些因素使磁性颗粒不可能全部都沿磁场方向排列为规则的直通链，不可避免地存在少数链，其排列方向不沿磁场方向，甚至无规则地弥散于磁流变液中。外界磁感应强度较小时，磁性颗粒远未达到磁饱和，此时磁场对磁流变液剪切应力的影响明显，而随着磁感应强度的增加，磁性颗粒逐渐达到磁饱和状态，其相互作用达到极值，从而使磁流变液也达到了剪切屈服应力。

由此，对磁流变液的成链机理的分析表明，在磁流变液中，磁性颗粒在磁场作用下，会由一种自由状态转变为链状，这为磁流变液产生剪切阻尼提供了理论依据。