速度和压强分布的分析介绍

（1）磁流变液通过平板间的速度和压强

基于平板模型，磁流变液在平行平板中流动的压降由两部分组成：内摩擦产生的压降及外加磁场产生的压降：

式中　Δp1——磁流变液在平板中流动的压降；

　　　Δpη——由于粘度而产生的压降；

　　　Δpτ（B）——由于磁场产生的压降；

　　　Ap——流体通过的横截面积；

　　　l，g0，w0——分别为简化模型的特征尺寸；

　　　v0——流体的初始速度；

　　　τy——与磁场相关的剪切屈服应力。

根据不同的流动特性，磁流变液在平板间的速度分为3 个部分：

相关参数详见参考文献[12]。

（2）磁流变液通过多孔介质的速度和压强

根据多孔介质的管束模型，将泡沫金属等效为等半径的毛细管束，流体通过毛细管横截面的平均流速与剪切应力及剪切速率的关系为(www.xing528.com)

式中　u——流体的平均流速；

　　　r——毛细管的半径；

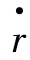　　　——流体的剪切速率；

　　　τ，τb——分别为半径为r 处流体的剪切应力和毛细管壁面的应力。

对于磁流变液，采用Bingham 本构模型：

得到剪切速率为

将式（3.23）代入式（3.21）并积分得到

式（3.24）即为磁流变液通过毛细管中的平均流速与毛细管壁面上的剪切应力τb 之间的关系。而在实际工程应用中需要知道的是流体通过毛细管的压强，为此，需要建立压降与剪切应力τb 之间的关系。

如前所述，磁流变液在毛细管中为稳定层流，则有：

将式（3.25）代入式（3.24），得到

式（3.26）即建立了磁流变液在毛细管中压降与平均流速的关系，其中R 与泡沫金属的孔隙率及渗透率相关。