FLUENT数值模拟流程建立几何模型和网格划分

基于FLUNT 的数值模拟过程如图3.4 所示。首先根据实际问题得到简化的几何模型，将几何模型划分为适合的网格，并将网格导入FLUENT 中，检查网格质量是否符合要求；设置相应流体的物性参数，选择合适的模型，并设置相应的初始条件及监测值，选择合理的离散化方式，初始化后求解；最后对得到的结果进行后处理，必要时需要重复上述过程，直至得到理想的结果。

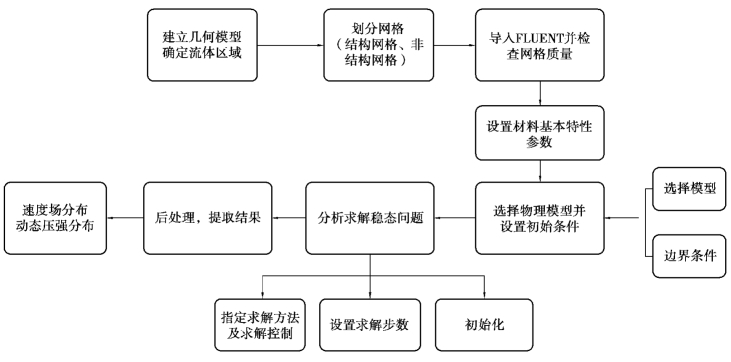
图3.4　FLUENT 数值模拟流程

（1）建立几何模型

图3.5 所示为采用WORKBENCH 13 中的DeignModeler 模块建立的物理模型，将其设为流体几何区域，中间1 mm 为多孔介质区域。

图3.5　几何模型

（2）划分网格

流动仿真中，网格质量直接决定了仿真结果的合理性。如果网格过多，虽然能够使计算结果更为准确，但计算量大，需要的计算时间过长；若网格太少，又有可能得不到合理的计算结果。因此，合理的网格不仅能够节省系统资源，而且有助于得到更加准确的模拟结果，同时也能加快收敛速度。为此，仿真前首先对网格无关性进行验证。为了检验网格独立性，仿真前采用FLUENT 的MESH 单元分别对模型进行粗糙网格划分（Coarse mesh）及精密网格划分（Fine mesh），不断调整单元网格的大小，直至零磁场时磁流变液的速度值变化范围在5%以内。经验证，发现单元数目为2 000 后，速度变化较小。于是，最终取单元网格大小为0.025 mm，单元数目为2 000。

（3）将网格导入FLUENT 并检查网格质量

查看并检查网格体积没有出现负网格，并且最小正交质量达到0.789，满足要求。

（4）设置材料基本特性参数

这里需要设置多孔介质区域及相应的孔隙率等参数。流体的流动方式采用雷诺数进行判断：

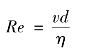
式中　v——磁流变液在泡沫金属中流动的平均速度；

　　　d 和η——分别为多孔泡沫金属的直径和磁流变液的运动粘度。

代入相关参数得到Re ＜2 300，因此，磁流变液在泡沫金属中的流动为层流。

为得到磁流变液在泡沫金属中的流动，还需要知道其黏性阻力和惯性阻力。磁流变液在多孔介质中的流动遵从Darcy 定律：

式中　Q——液体的流量；

　　　A——多孔介质的横截面积；

　　　k——多孔介质的渗透系数；(www.xing528.com)

　　　Δp，l——分别为多孔介质两端的压力差和多孔介质的厚度；

　　　η——液体的粘度。

流体在多孔介质中流动，根据惯性损失的达西定律：

式中　Ri——惯性阻力；

　　　L——材料的特征长度；

　　　vs——速度；

　　　ρ——流体密度。

多孔材料的孔隙率和渗透率与黏性阻力及惯性阻力由Ergun 等式描述：

式中　D——孔直径；

　　　ε——孔隙率；

　　　ψ——孔圆度（刻画孔接近圆孔程度的大小，孔圆度越大越好）；

　　　Rv 和Ri——分别为黏性阻力系数和惯性阻力系数。

代入数值，得到黏性阻力系数Rv=1.87 ×107。由于磁流变液在孔内层流，惯性阻力系数Ri=0。

（5）边界条件

入口及出口都设置为压强边界，且壁面无滑移。

（6）设置求解方式

由于磁流变液在泡沫金属中的流动速度较小，而且为不可压缩稳定层流，因此，FLUENT中采用默认的基于压力求解器SIMPLE 的算法，当计算到0.001 时收敛，同时，给定初速度为1 m/s，求解并建立速度和压强的监控面。

（7）结果后处理

ANSYS 流场分析的后处理软件CFD-POST 与FLUENT 无缝连接，提供了丰富的绘图格式，包括x-y 曲线图，多种格式的2D 图形、3D 剖面图和3D 立体图。

综上所述，相关参数设置如下：磁流变液密度为2 650 kg/m3，采用Bingham 模型；泡沫金属的孔隙率为85%。采用不可压缩稳定层流模型、压力入口及压力出口边界条件，出口处作为参考点大气压强，并利用二阶迎风策略求解动量方程。入口处初始压强为50 Pa，初始速度为1 m/s。表面张力系数设为60 mN/m。考虑重力作用，并设重力加速度沿x 轴负方向，即g= -9.81 m/s2。