蠕变模型是指在试验的基础上，采用数学的方法，描述材料的蠕变变形随时间的变化关系。在土力学中，建立蠕变模型的方法主要有两种：一种是理论模型方法，将所分析的对象视为介于欧几里得刚体（绝对刚体）和帕斯卡流体（不可压缩液体）之间的物质，采用胡克弹性体、牛顿黏滞体和圣维南塑性体这几个不同元件的组合，可以形成不同的流变模型。常用的流变模型有马克斯威尔（Maxwell）模型（虎克弹性体串联牛顿黏滞体）、宾哈姆（Bingham）模型（圣维南塑性体并联牛顿黏滞体）、开尔文（Kelvin）模型（虎克弹性体并联牛顿黏滞体）等。另一种方法为经验函数方法，通过试验获得材料变形随时间的变化，绘出蠕变和时间的关系曲线，然后选择合适的数学函数（通常为衰减函数）来拟合试验曲线。
目前，对于堆石蠕变变形的描述，通常采用经验函数的方法，为简化起见以采用单项函数的方式居多，常用的函数形式包括指数型、幂函数型、双曲线型、对数型等。
根据九甸峡主堆石蠕变试验的结果，发现堆石的蠕变量与时间在双对数坐标系下呈现较好的线性关系。因此，可以采用幂函数来表达堆石体蠕变量与时间的相关关系，即ε＝αtβ，其中α可以理解为某一应力状态下的主压缩变形量，也就是通常意义上的弹塑性变形。此后发生的变形与时间有关，即为蠕变。
（1）轴向蠕变
对各不同围压、不同偏应力下试样的轴向蠕变曲线采用幂函数进行拟合，得到拟合参数α1、β1，见表4.5-1。
表4.5-1 轴向蠕变幂函数拟合参数
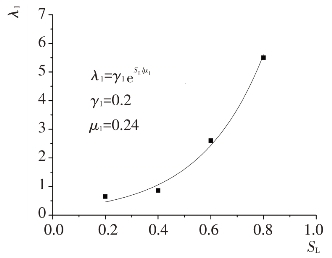
不同应力水平的蠕变初始量与围压的关系拟合曲线见图4.5-22。α1值随围压的增大而增大，并与围压呈较好的线性关系，因此，拟合表达式可确定为α1=λ1σ3，并可得到参数λ1，见表4.5-2。系数λ1与应力水平SL之间的关系见图4.5-23。通过观察和分析，本研究采用拟合表达式
，并得到参数γ1、μ1，见图4.5-23。
图4.5-22 不同应力水平的轴向蠕变初始量与围压关系曲线
表4.5-2 参数λ1数值
(www.xing528.com)
图4.5-23 参数λ1与应力水平关系曲线
（2）体积蠕变
对各不同围压、不同偏应力的体积蠕变曲线采用幂函数进行模拟，得到拟合参数αV、βV，见表4.5-3。
表4.5-3 体积蠕变幂函数拟合参数
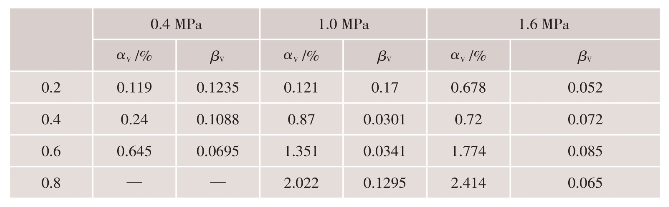
从参数中可以看出α1值随围压和应力水平的增大而增大，不同应力水平的蠕变初始量与围压的关系拟合曲线见图4.5-24。αV与围压呈较好的线性关系，拟合表达式可确定为αV=λVσ3，得到参数λV，见表4.5-4。
系数λV与应力水平SL之间的关系见图4.5-25，采用拟合表达式λV=γVSL，可得到参数γV。
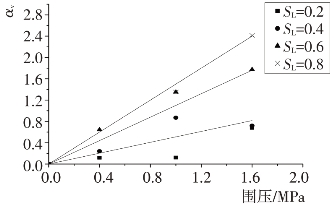
图4.5-24 不同应力水平的体积蠕变初始量与围压关系曲线
表4.5-4 参数λV
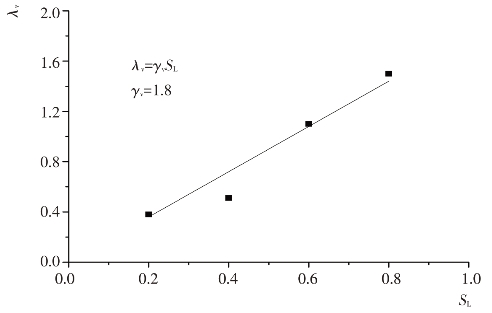
图4.5-25 参数λV与应力水平关系曲线
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
