(1)最大动剪模量
试验采用往返加荷三轴试验并结合激光微小应变测试系统进行试验。根据试验结果可整理出试验材料的最大动剪模量Gmax与平均有效主应力σ0′=(s1′+s3′)/2之间的关系曲线,见图4.4-6至图4.4-9。
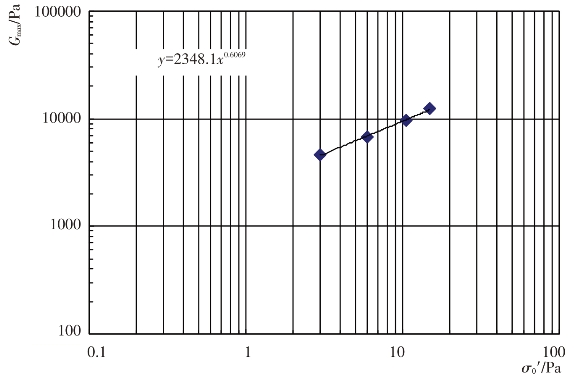
图4.4-6 砂卵砾石料Gmax-σ0′关系(Kc=2.0)
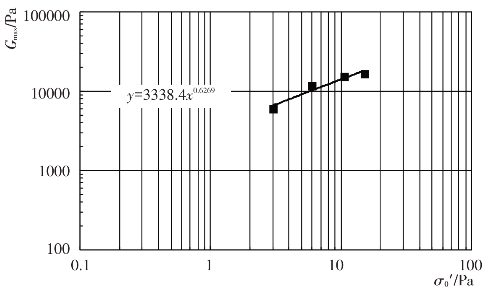
图4.4-7 过渡料Gmax-σ0′关系(Kc=2.0)
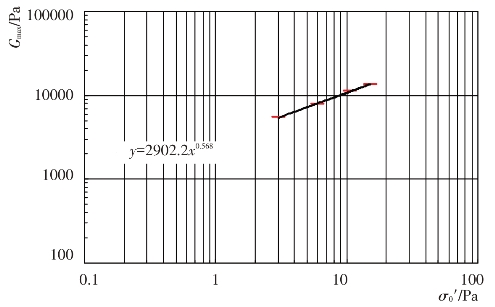
图4.4-8 主堆石料Gmax-σ0′关系(Kc=2.0)
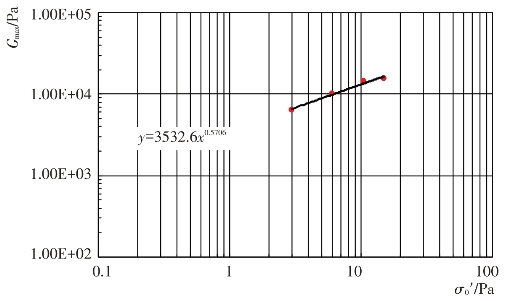
图4.4-9 垫层料Gmax-σ0′关系(Kc=2.0)
最大动剪模量Gmax与平均有效主应力σ0′之间可以用如下的幂函数形式表示:
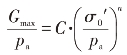
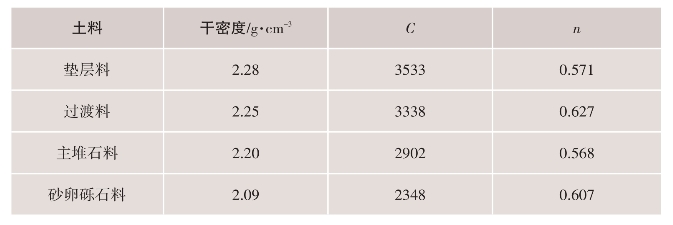
式中:pa为大气压力。动剪模量系数C与指数n由试验确定,试验结果见表4.4-7。
表4.4-7 动剪模量系数C与指数n试验结果
(2)动剪模量及阻尼比与动剪应变
试验给出了试验土料的动剪模量比G/Gmax及阻尼比λ与动剪应变幅γ的变化关系,见图4.4-10至图4.4-17。由图可见,当γ达到一定值之后,G/Gmax随γ的增大而衰减,随围压力σ0′的增大而增大。λ随γ的增大而增大,随σ0′的增大而减小。这些变化关系反映了试验土料在动荷载作用下应力-应变关系的非线性与黏滞性特征。
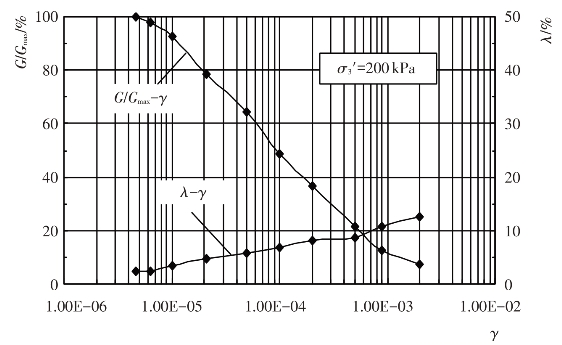
图4.4-10 垫层料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
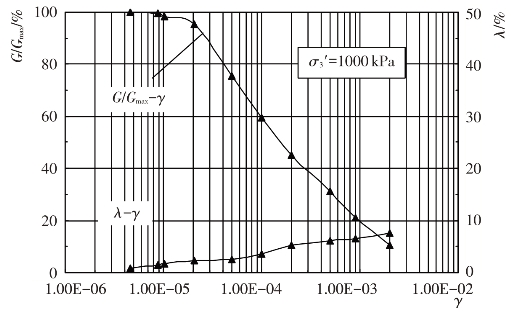
图4.4-11 垫层料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
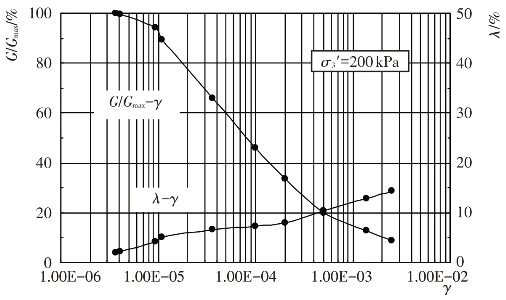
图4.4-12 过渡料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
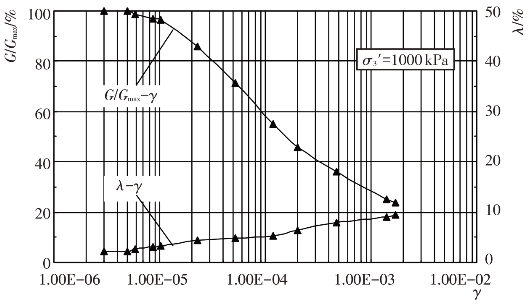
图4.4-13 过渡料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
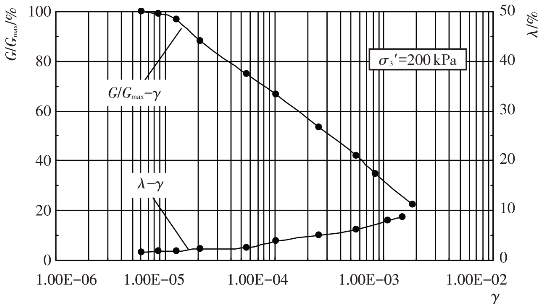
图4.4-14 主堆石料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
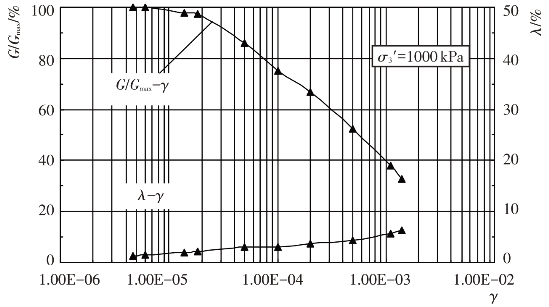
图4.4-15 主堆石料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
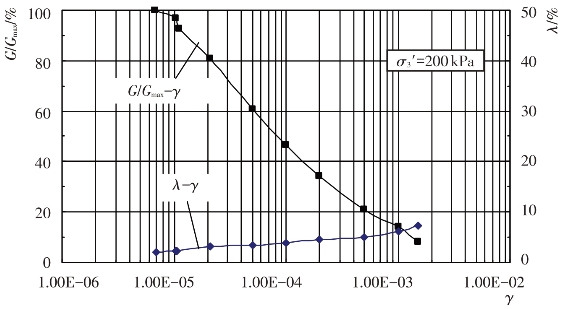
图4.4-16 砂卵砾石料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
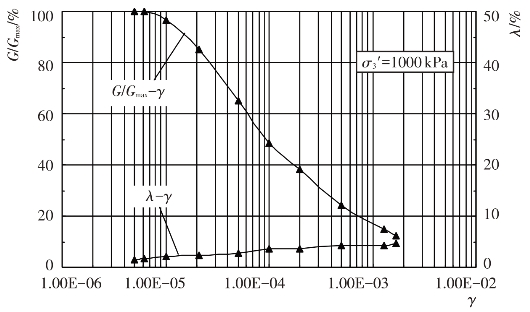
图4.4-17 砂卵砾石料G/Gmax-γ、λ-γ关系曲线(Kc=2.0)
各土料试验结果的数据分别列于表4.4-8~表4.4-11。
表4.4-8 垫层料应变效应的数值化结果(Kc=2)
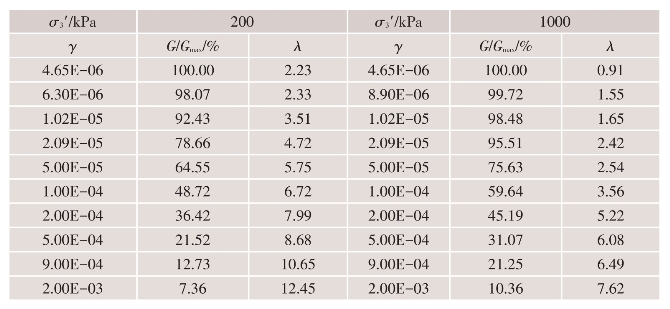
表4.4-9 过渡料应变效应的数值化结果(Kc=2)
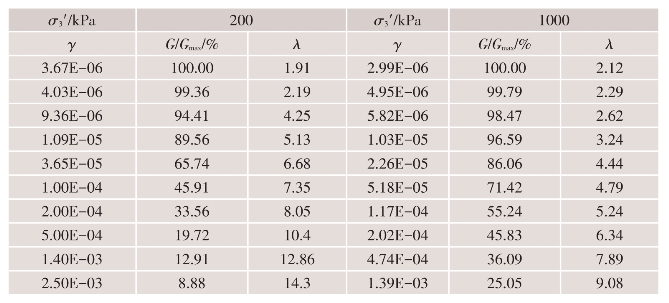
表4.4-10 主堆石料应变效应的数值化结果(Kc=2)
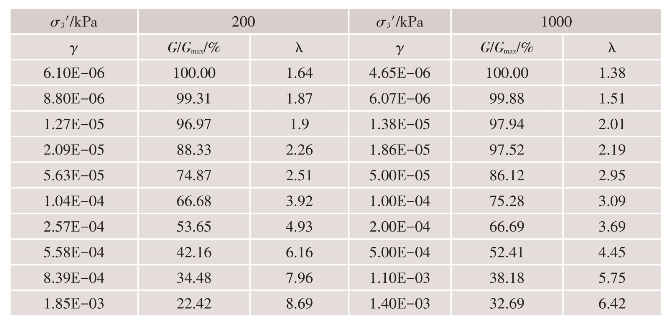
表4.4-11 砂卵砾石料应变效应的数值化结果(Kc=2)
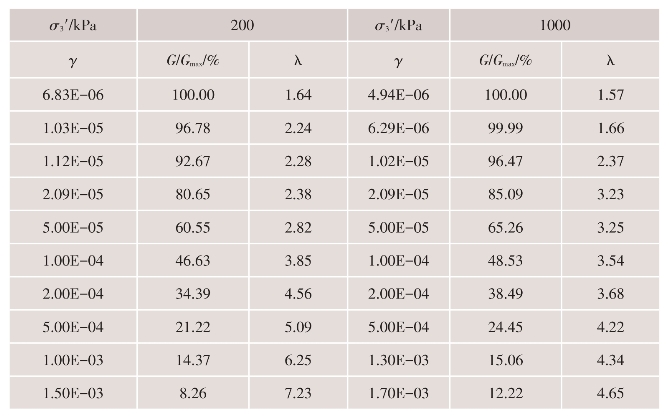
(3)动强度
动强度试验采用固结比Kc为2,围压力σ3′分别为200 kPa和1000 kPa。根据往返加荷试验过程中所得到的试样动应力过程线、动孔压过程线和动变形过程线,以轴向应变εa=5%作为试样的破坏标准,即可整理出坝基砂卵砾石料的动剪应力比Δτ/σ0′与破坏振次Nf的关系曲线,见图4.4-18。其中Δτ为动三轴试验中试样45°剪切面上的动剪应力,σ0′=(σ1′+σ3′)/2为试样45°剪切面上的初始有效法向应力,σ1′和σ3′分别为试样固结时的有效大、小主应力。
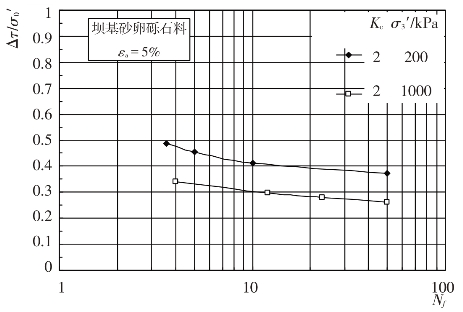
图4.4-18 Δτ/σ0′-Nf关系曲线
由图4.4-18可见,动强度大小与破坏周数有关,周数越大,动强度越小。对应于破坏周数Nf的试验结果列于表4.4-12。
表4.4-12 坝基砂卵砾石料动强度试验结果
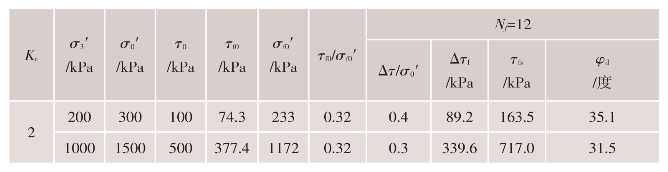
实际的地震荷载为随机荷载,试验确定动强度时采用的是等效循环荷载,与等效循环周数Neq相应的等幅剪应力为地震产生的最大剪应力的65%。考虑到九甸峡水利枢纽工程区域的地震震级为7级,等效循环周数Neq取12周。
坝基砂卵砾石料在不同的初始应力条件下,相应于等效循环破坏周数的潜在破坏面上地震总应力抗剪强度τfs与初始有效法向应力σf0′的关系,根据参考文献按如下换算公式确定:
σf0′=σ0′-τ0·sin φ′
τf0=τ0cos φ′
α=τf0/σf0′
(Δτ)fn=(Δτ/σ0′)n·σ0′·cos φ′
τfs=(Δτ)fn+τf0
其中,τ0=(σ1′-σ3′)/2为试样45°剪切面上的初始剪应力,α为试样潜在破坏面上的初始剪应力比,(Δτ/σ0′)n为相应于某等效循环周数Neq时试样45°剪切面上的动剪强度比,φ′为试样的有效应力内摩擦角,可取静力试验的相应值,(Δτ)fn为相应于某等效循环周数Neq时试样潜在破坏面上的动剪应力,τf0为试样潜在破坏面上的初始剪应力,其余符号同前。
根据试样在饱和固结不排水条件下的往返加荷三轴试验所得的动应力、动孔压和动变形过程线,可以整理出坝基砂卵砾石料在不同初始应力和动剪应力比Δτ/σ0′条件下动孔压比ud/σ0′与往返加荷振动周数N的关系曲线,见图4.4-19和图4.4-20。试验结果表明,初始应力条件、往返加荷振动周数和动剪应力比Δτ/σ0′对动孔压比ud/σ0′的发展变化都有一定的影响,在初始固结应力和往返加荷振动周数一定的条件下,动孔压比随动剪应力比的增大而增大。同时,还可以看出,在初始固结应力条件和动剪应力比Δτ/σ0′一定时,达到一定的振动周数N后,动孔压比ud/σ0′不再随动剪应力比的增大而增大,而是趋于一个稳定值。坝基砂卵砾石料动孔压比与动剪应力比的关系曲线见图4.4-21。可以看出,在固结比和动剪应力比一定的条件下,动孔压比随围压力的增大而增大。
根据坝基砂卵砾石料试样在饱和固结不排水条件下的往返加荷三轴试验所得的动应力和动变形过程线,整理出了坝基砂卵砾石料在不同初始应力和动剪应力比Δτ/σ0′条件下轴向总应变Δεa与往返加荷振动周数N的关系曲线,见图4.4-22和图4.4-23。试验结果表明,在初始固结应力和往返加荷振动周数一定的条件下,轴向总应变Δεa随动剪应力比的增大而增大。图4.4-24中给出了坝基砂卵砾石料轴向总应变Δεa与动剪应力比的关系曲线。可以看出,在固结比和动剪应力比一定的条件下,轴向总应变Δεa随围压力的增大而增大。
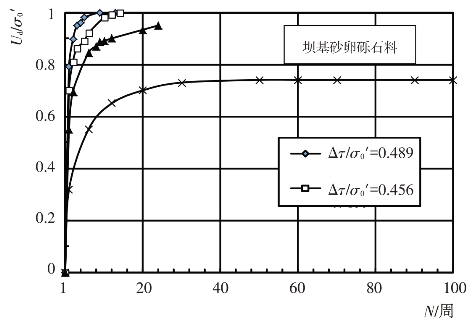
图4.4-19 ud/σ0′-N关系曲线
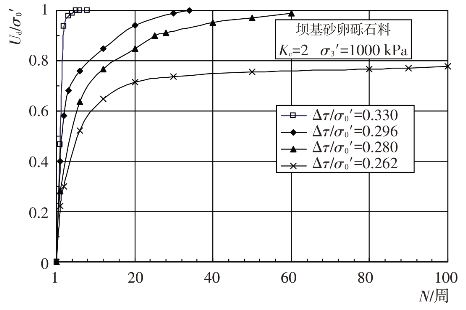
图4.4-20 ud/σ0′-N关系曲线
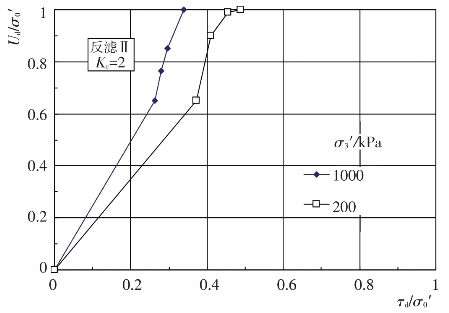
图4.4-21 ud/σ0′-τd/σ0′关系曲线(N=12)
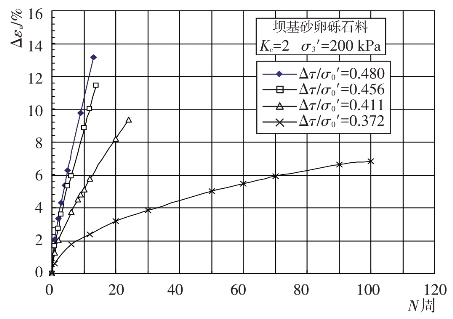
图4.4-22 Δεa-N关系曲线
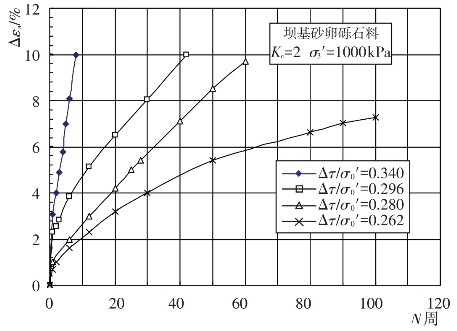
图4.4-23 Δεa-N关系曲线
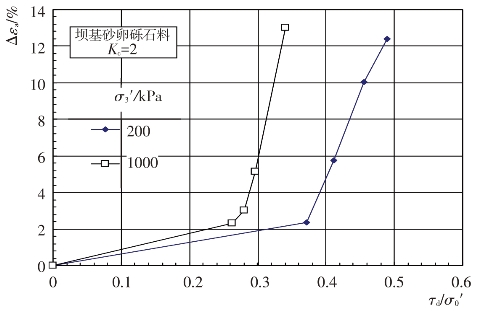
图4.4-24 Δεa-N关系曲线
(3)残余变形(https://www.xing528.com)
土石材料在振动荷载下的残余体应变和残余轴应变的大小与等效振次有关,等效振次取决于地震震级,九甸峡坝料的动力残余变形试验按12次和20次对试验结果进行了整理,对应的地震震级分别为7级和7.5级。
根据试验结果,可以整理出不同固结应力条件和动剪应力作用下主堆石料、垫层料、过渡料和坝基砂卵砾石料的残余体应变εdv随振动次数N的关系,见图4.4-25至图4.4-28。
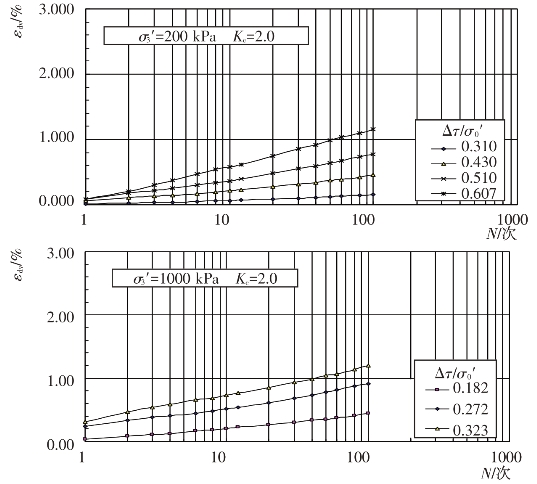
图4.4-25 主堆石料残余体积应变与振次的关系曲线

图4.4-26 垫层料残余体积应变与振次的关系曲线
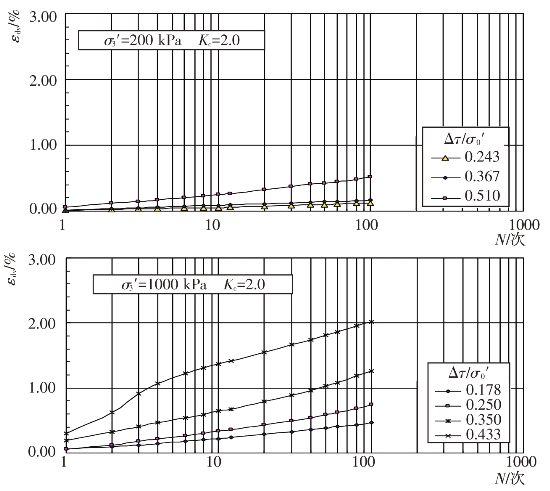
图4.4-27 过渡料残余体积应变与振次的关系曲线
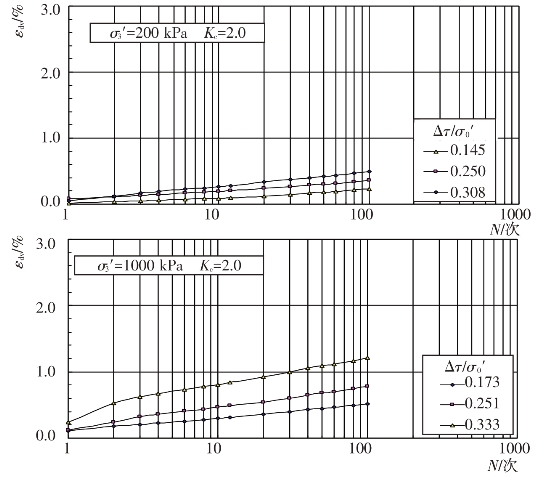
图4.4-28 坝基砂卵砾石料残余体积应变与振次的关系曲线
由图可见,残余体应变εdv与土的类型、固结应力条件和动剪应力Δτ等有关。在一定的固结应力条件和动剪应力作用下,残余体应变εdv随振动次数N的增大而增大。固结应力条件和振动次数N一定时,作用在试样上的动剪应力越大,所引起的残余体应变εdv越大。
根据上述残余体应变εdv与振动次数N的关系曲线,可分别整理出主堆石料、垫层料、过渡料和坝基砂卵砾石料的残余体应变εdv与动剪应力Δτ关系曲线,见图4.4-29至图4.4-32。进一步整理成残余体应变εdv与动剪应力比Δτ/σ0′的关系曲线,见图4.4-33至图4.4-36。从图中可以看出固结应力条件和动剪应力Δτ对残余体应变εdv的影响。当固结应力条件一定时,残余体应变εdv随动剪应力的增大而增大。当固结比Kc一定时,在相同的动剪应力作用下,围压力σ3′越大,残余体应变εdv越小。根据试验结果,残余体应变εdv与动剪应力比Δτ/σ0′的关系可用幂函数形式近似表示如下:
εdv=K(Δτ/σ0′)n
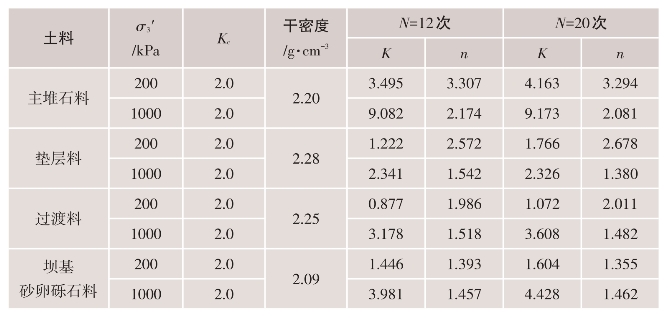
式中,K、n分别为与土性、应力状态及振次N有关的系数和指数,由试验结果确定,N=12和20时不同固结应力条件下的系数和指数值见表4.4-13,残余体应变εdv单位为%。
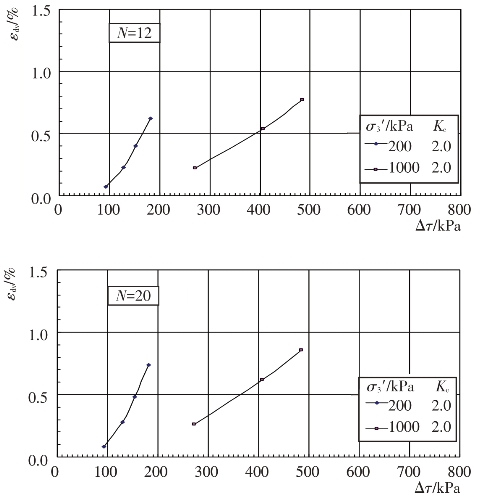
图4.4-29 主堆石料残余体应变与剪应力的关系曲线
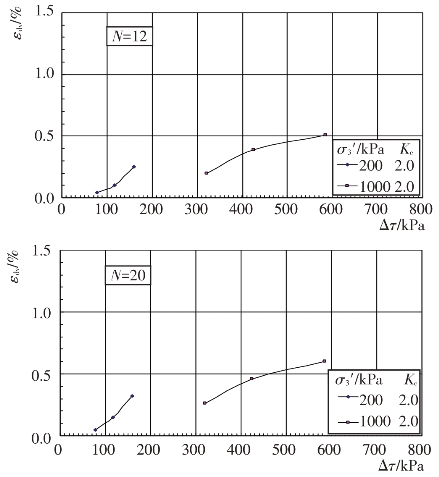
图4.4-30 主堆石料残余体应变与剪应力的关系曲线
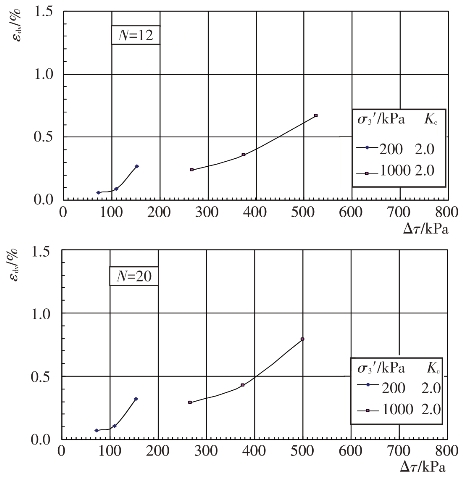
图4.4-31 过渡料残余体应变与剪应力的关系曲线
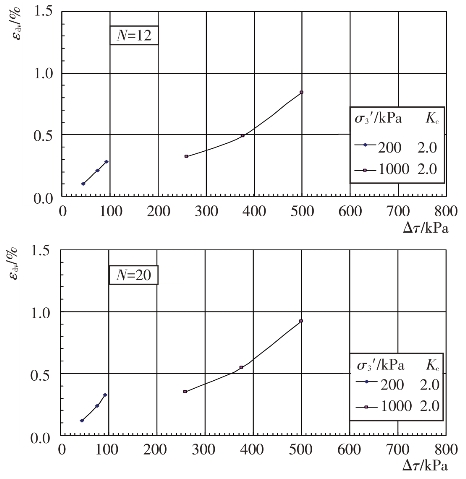
图4.4-32 坝基砂卵砾石料残余体应变与剪应力的关系曲线
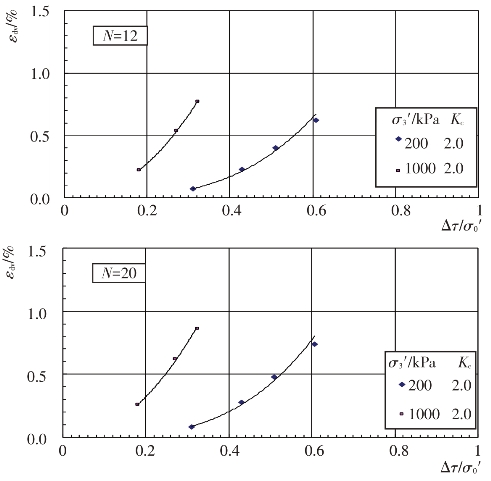
图4.4-33 主堆石料残余体应变与动剪应力比的关系曲线
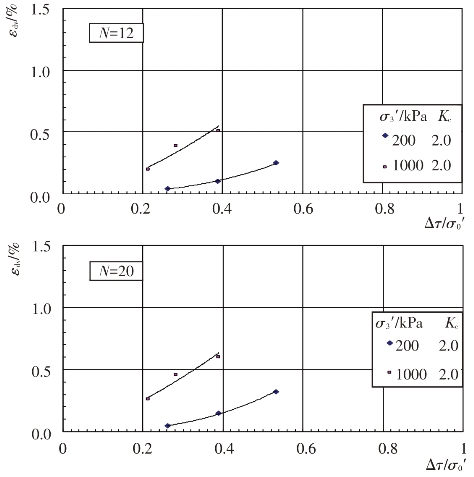
图4.4-34 垫层料残余体应变与动剪应力比的关系曲线
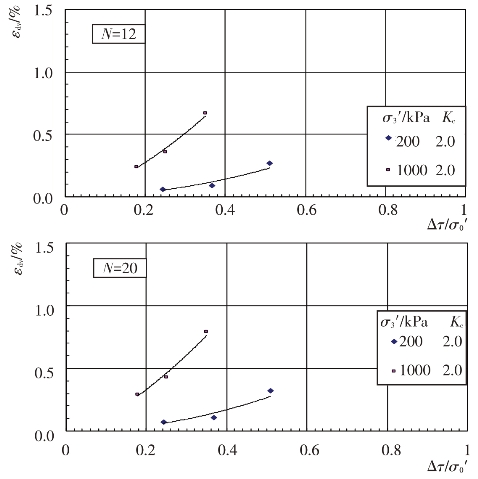
图4.4-35 过渡料残余体应变与动剪应力比的关系曲线
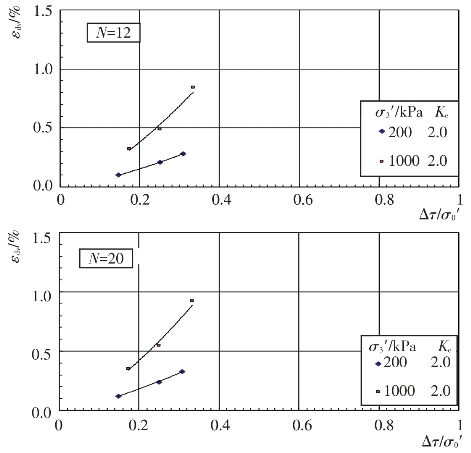
图4.4-36 坝基砂卵砾石料残余体积应变与动剪应力比的关系曲线
表4.4-13 残余体应变系数和指数
不同固结应力条件和动剪应力作用下主堆石料、垫层料、过渡料和坝基砂卵砾石料的残余轴应变εp随振动次数N的变化关系见图4.4-37至图4.4-40。根据残余轴应变εp与振动次数N的关系曲线,可分别整理出不同等效振次条件下残余轴应变εp与动剪应力Δτ及残余轴应变εp与动剪应力比Δτ/σ0′的关系曲线,见图4.4-41至图4.4-48。可以看出残余轴应变随动剪应力的变化与残余体应变有基本类似的规律。
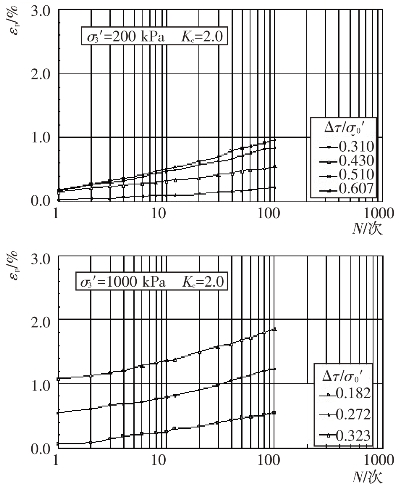
图4.4-37 主堆石料残余轴应变与振次的关系曲线
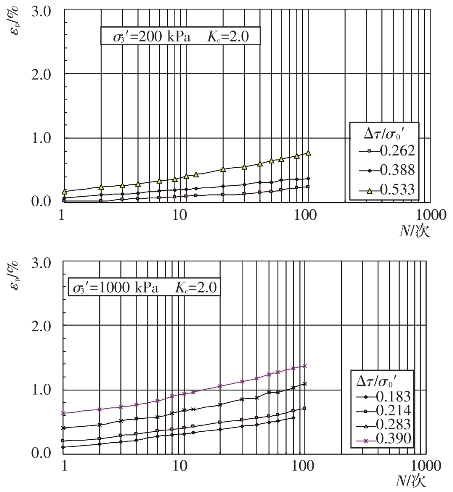
图4.4-38 垫层料残余轴应变与振次的关系曲线
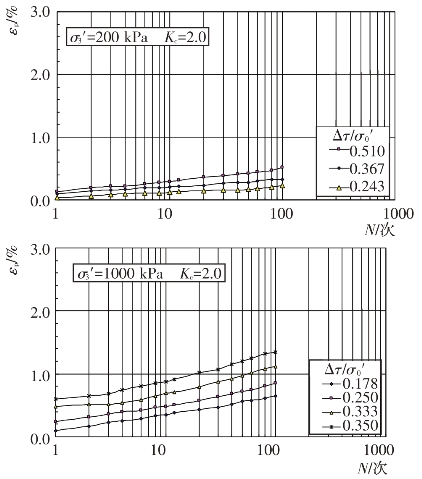
图4.4-39 过渡料残余轴应变与振次的关系曲线
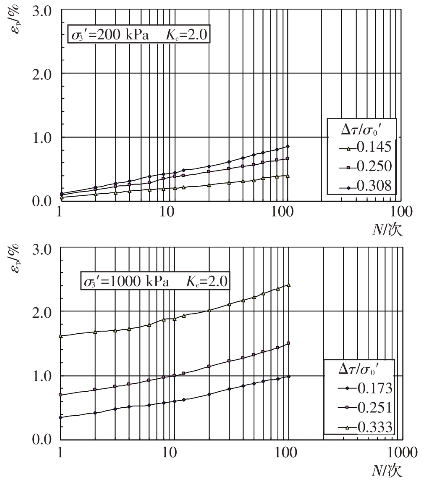
图4.4-40 坝基砂卵砾石料残余轴应变与振次的关系曲线
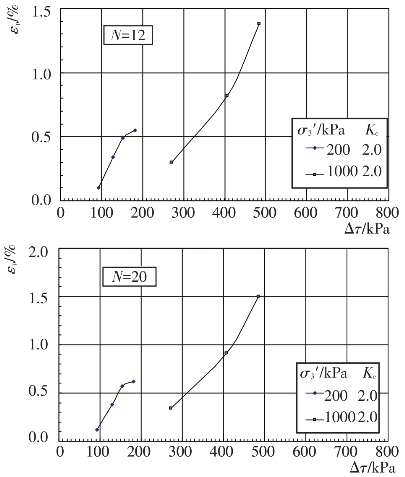
图4.4-41 主堆石料残余轴应变与动剪应力的关系曲线
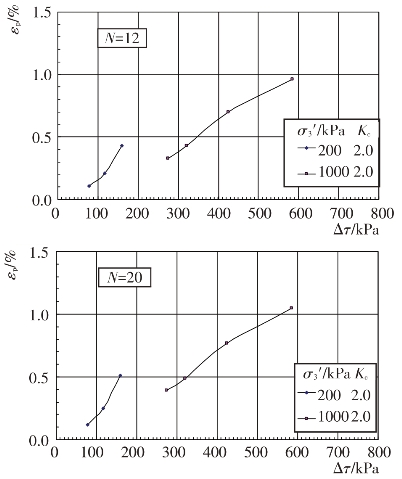
图4.4-42 垫层料残余轴应变与动剪应力的关系曲线
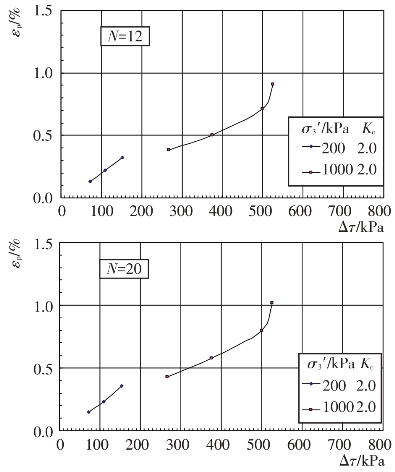
图4.4-43 过渡料残余轴应变与动剪应力的关系曲线
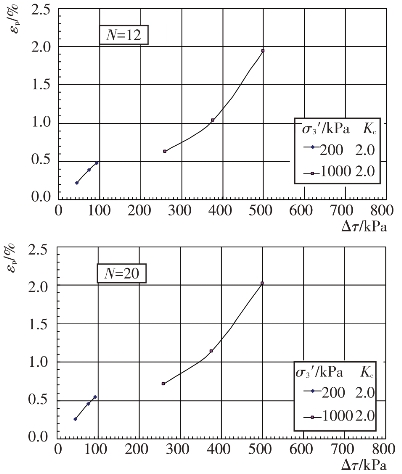
图4.4-44 坝基砂卵砾石料残余轴应变与动剪应力的关系曲线
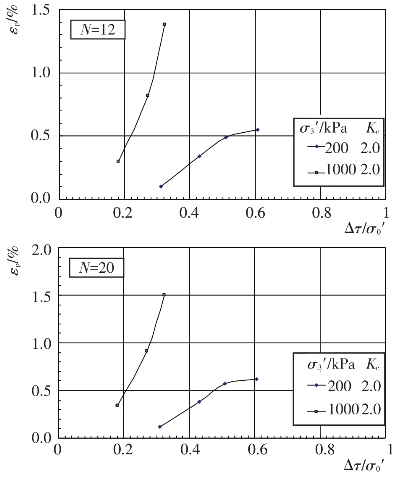
图4.4-45 主堆石料残余轴应变与动剪应力比的关系曲线
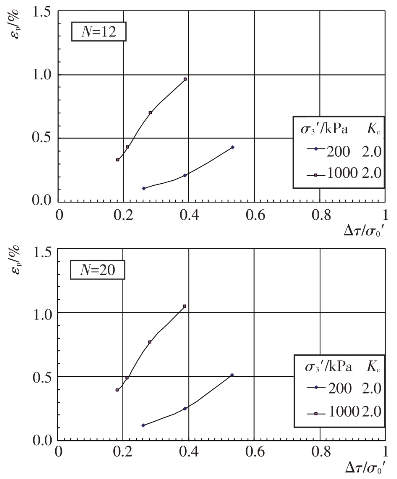
图4.4-46 垫层料残余轴应变与动剪应力比的关系曲线
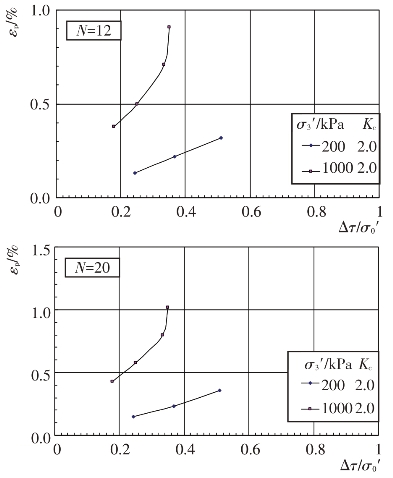
图4.4-47 过渡料残余轴应变与动剪应力比关系曲线
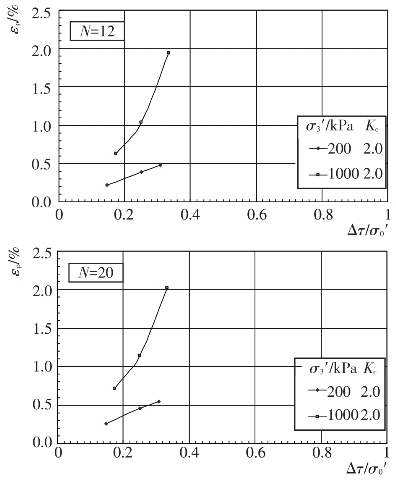
图4.4-48 坝基砂卵砾石料残余轴应变与动剪应力比关系曲线
残余轴应变εp与残余剪应变γp之间的关系可用式γp=(1+μ)εp表示,μ为动波松比,取值为0.35。残余剪应变γp与动剪应力Δτ之间的关系可近似地用双曲线形式来表述:
Δτ=γp/(a+bγp)
将纵轴改为γp/Δτ,则γp/Δτ与γp的关系就成为一条直线,见图4.4-49至图4.4-52。
γp/Δτ=a+bγp
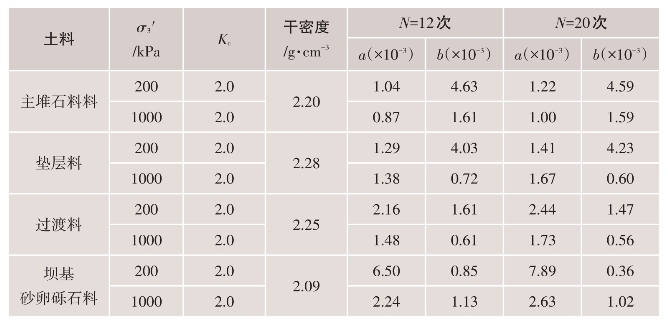
式中,a和b为试验常数。它们与试验土料的类型、固结应力条件σ3′、Kc和振动次数N有关,由试验结果整理出a和b值见表4.4-14。残余剪应变γp的单位为%。
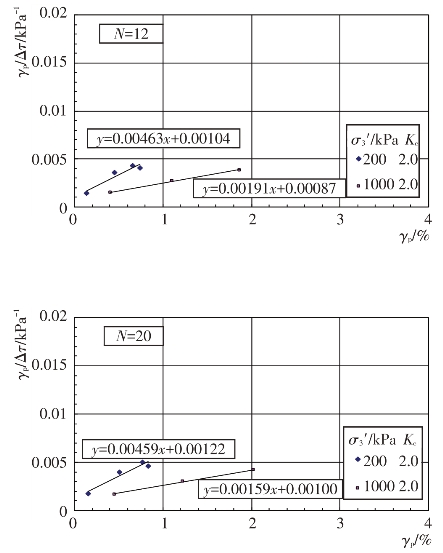
图4.4-49 主堆石料γp/Δτ与γp关系曲线
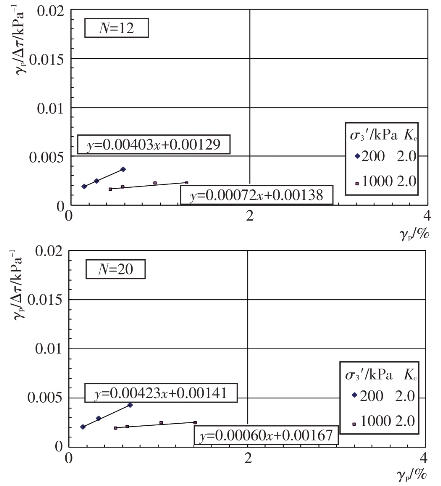
图4.4-50 垫层料γp/Δτ与γp关系曲线
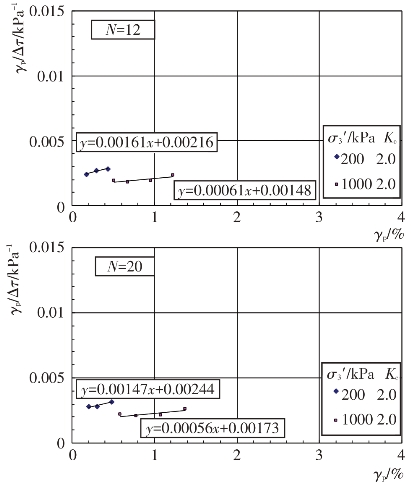
图4.4-51 过渡料γp/Δτ与γp关系曲线
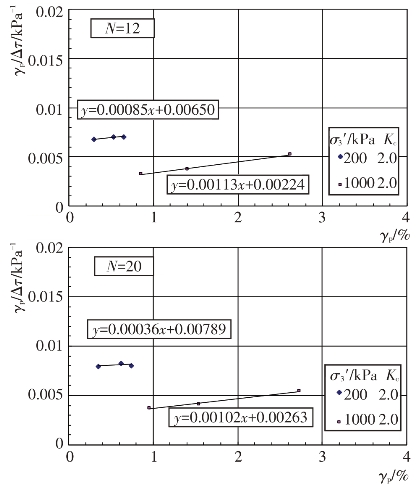
图4.4-52 坝基砂卵砾石料γp/Δτ与γp关系曲线
表4.4-14 残余剪应变参数a、b值
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




