高度函数法：利用相对高度差排样

分析毛坯排样时冲裁件图形的位置特点可知，在排样图上各图形的轴线总是相互平行的（图8-15）。如前所述，在一般的排样方法中以φ和λ为参数进行优化。高度函数法则是根据图形轴线的平行性，采用各图形的相对高度差h_ij为优化排样参数。在图8-15所示的双排排样中，以h₁₂和h₂₃为排样参数。

参数φ和λ与参数h₁₂和h₂₃之间存在以下关系：

φ=π/2-arctan（h/r） （8-1）

λ=h₁₂sinφ-r₁₂cosφ （8-2）如图8-15所示，在排样中各个图形均置于其自身坐标系中，第一、第二和第三图形的坐标系分别为x₁O₁y₁、x₂O₂y₂和x₃O₃y₃。r₁₂和h₁₂为第二图形自身坐标系原点在第一图形自身坐标系中的坐标。r₂₃和h₂₃为第三图形坐标系原点在第二图形坐标系中的坐标。式（8-1）中，h为h₁₂与h₂₃的代数和，表示O₃点到x₁轴的距离；r为y₃轴与y₁轴的间距，其值为

r=max{[r₁₂（h₁₂）+r₂₃（h₂₃）]，r₁₃（h）} （8-3）

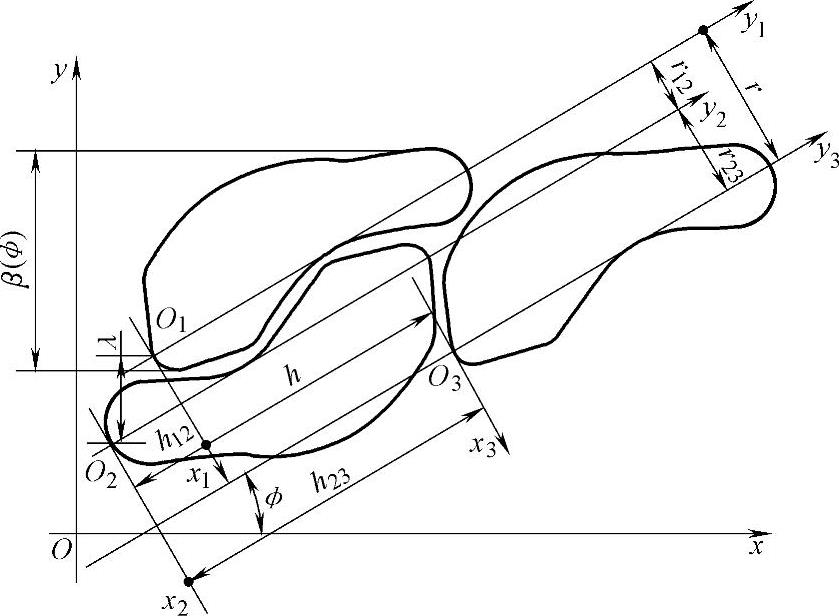
图8-15 排样中图形间的关系

1.可行域与相切条件

设图形在其自身坐标系中包括搭边值在内的高度为t（图8-16），则搜索最优排样方案的可行域为

G{-t≤h₁₂≤t，-t≤h₂₃≤t}因为各图形自身坐标的y轴在排样图中相互平行，各图形的高度皆为t，所以G为方形域。

如果将可行域等分网格数定为2m×2m，则搜索时h₁₂和h₂₃每次变化的量Δt=t/m。程序分两次优化，第一次为初步优化，第二次为细分优化，即在第一次求得的最优值附近细分网格，进一步搜索。设第一次优化求得的最优值为h₁₂和h₂₃，第二次优化时的搜索区域为

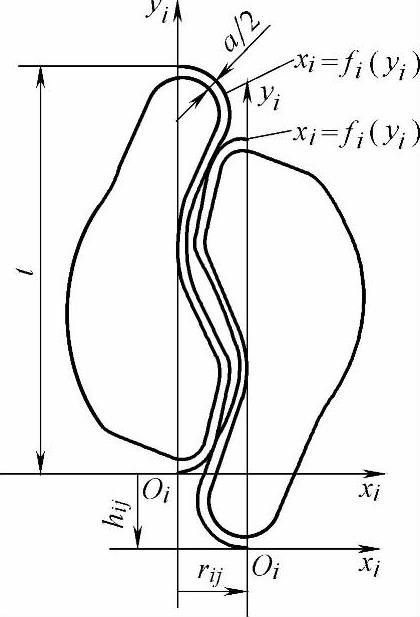
图8-16 两图形相切时的关系

G′{h₁₂-Δt≤h₁₂′≤h₁₂+Δt，h₂₃-Δt≤h₂₃′≤h₂₃+Δt}通过两次搜索，求得的最优值已相当精确。

为了获得排样方案，通常将图形等距放大半个搭边值，在排列图形时使相邻的放大图形相切。确定两图形相切的算法对于优化排样的速度有重要影响。在图8-16中，两图形置于自身的坐标系x_iO_iy_i和x_jO_jy_j中。图形以其最高点和最低点为界分为两部分，设图形i的右半部分的曲线为x_i=f_i（y_i），图形j的左半部分曲线为x_j=f_j（y_j）。当两图形相切时，存在如下关系：

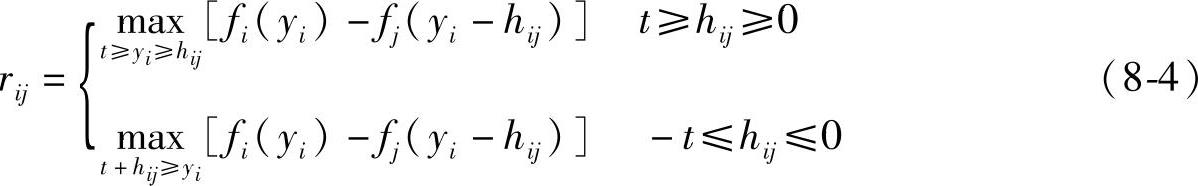
式中，r_ij为O_j在x_iO_iy_i坐标系中的横坐标。利用式（8-4）的关系，可以预先在h₁₂、h₂₃和h₁₃的等分点上算出r₁₂、r₂₃和r₁₃的值，并列成数据表。在排样过程中可直接调用这些数值，因而提高了效率。

这种确定两图形相切的方法与加密点排样法采用的算法类似，在确定图形相切时避免了计算量很大的迭代运算。但是，应该指出的是，这种方法对于凸图形是完全正确的，对于具有凹下部分的图形在绝大多数情况下也可找到最优值，但在个别情况下可能丢失最优解。正如绝大多数优化方法都有其一定的适用范围，这种方法也有其适用范围，但是其运行速度快，计算效率高，所以仍不失为一种好的排样方法。

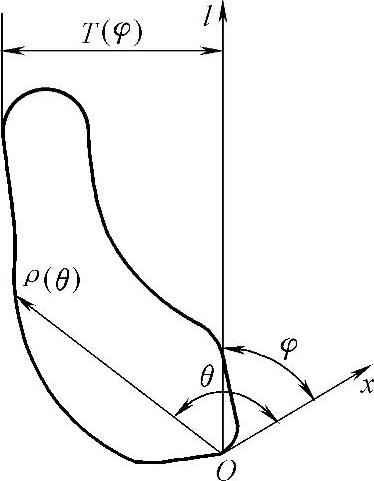
图8-17 高度函数的定义

2.条料宽度、步距和材料利用率的计算

如图8-17所示，将图形放置在极坐标系中，极坐标系原点与其自身参考坐标系原点重合，x轴方向与自身参考坐标系的x_i轴方向一致，图形的轮廓曲线为ρ（θ）。设代表排样条料方向的l轴与x轴之间的夹角为φ，则图形轮廓和l轴的最大距离为(www.xing528.com)

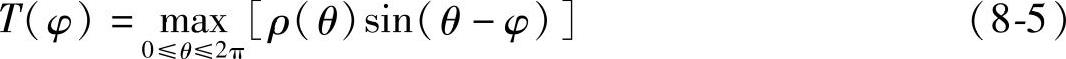
这里，将T（φ）定义为高度函数。

在图8-15中，φ角可由式（8-1）确定，排样条料方向与图形自身坐标系x_i轴的夹角为

因此，条料的宽度B可用下式计算，

式中 T₁、T₂——第一图形和第二图形的高度函数；

a——搭边值。

因为在工件的等距放大图中放大量的a/2（图8-16），所以式中应包括搭边值a。如果考虑到工件间的搭边和侧搭边不同，可对此项进行修正。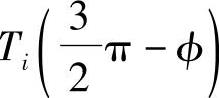表示图形i的下半部轮廓和参考轴l_i之间的最大距离。λ按（8-2）计算，因为λ值表示工件2相对于工件1的错移量，所以其值有正负之分。

参考图8-15，不难得出计算进给步距H的公式：

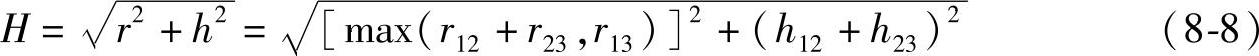
所以，条料的步进材料利用率η可用下式计算，

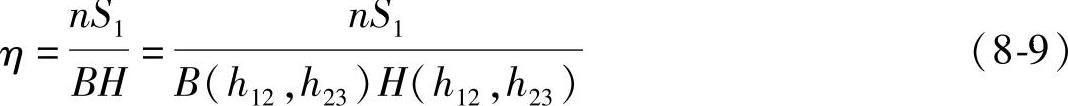
式中 S₁——一个零件的面积；

n——排样的排数。

条料的宽度B和进给步距H皆为h₁₂和h₂₃的函数，可用式（8-7）和式（8-8）计算。

3.排样过程

高度函数法的排样过程如图8-18所示。排样前首先进行数据处理，将图形信息转换成便于排样的数据形式。前置数据处理包括输入图形信息和排样方式，计算图形的面积，选取搭边值，并以二分之一的搭边值等距放大图形。对放大处理后的图形作多边形化处理，建立图形的自身坐标系。根据式（8-5）建立图形的高度函数表，以便于排样过程中调用。变量φ在其变化域[0，2π]内的等分数取为128，计算精度取为搭边值的5%。

数据准备完毕后，在h₁₂和h₂₃的变化域划分网格。为了在排样过程中快速使图形相切，在h₁₂和h₂₃的等分点上按式（8-4）计算r_ij的值，并列成数表。排样时用查表法可以很快求得B和H的值。在程序中进行了两次优化，首次优化搜索整个方形域G，获得初步最优方案。然后，在最优解附近确定搜索区域G′，并在此区域内以较小步距搜索，最终获得较精确的最优解。程序中将G域的边长分为50等份，将G′域的边分为20等份。在IBM PC计算机上运行，3～5min便可完成优化排样。

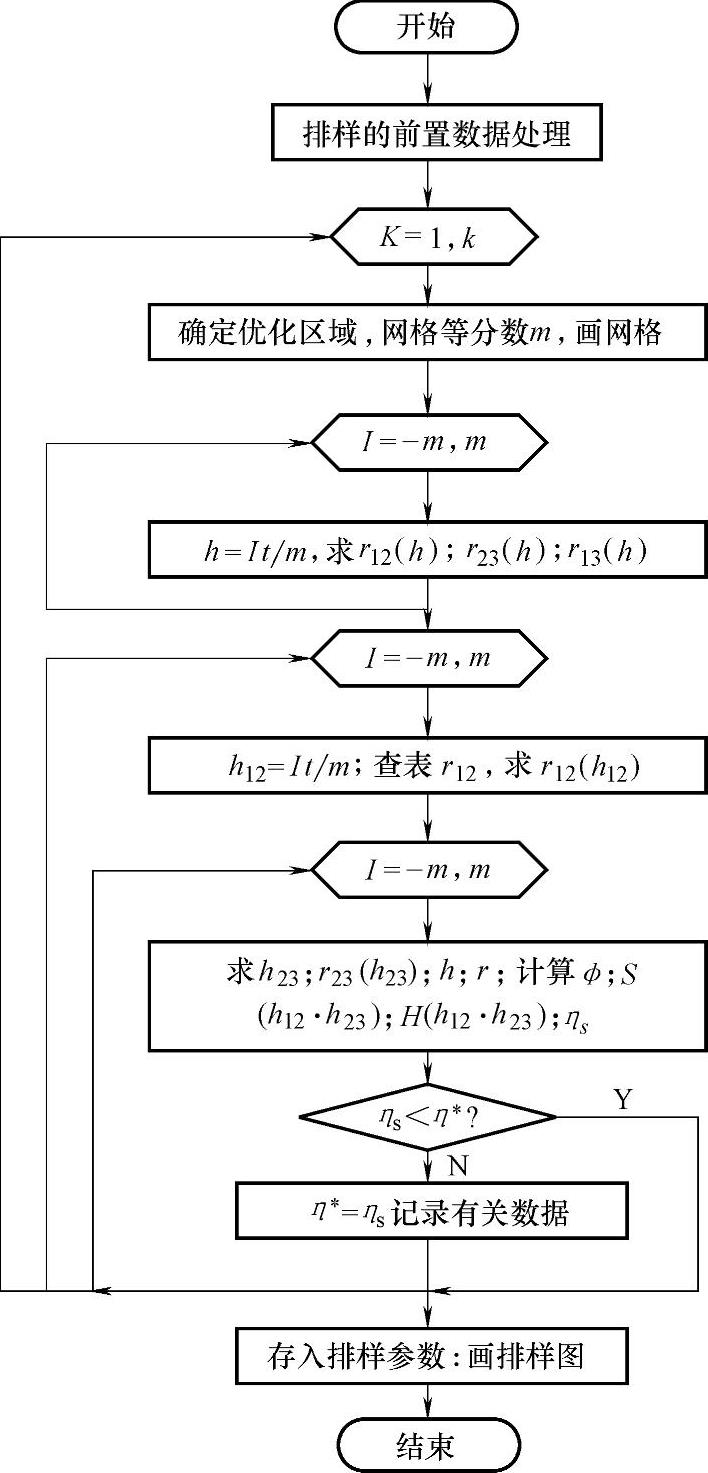
图8-18 高度函数法的排样过程