数学描述：毛坯排样问题的解决方案

图8-11为实际生产中常用的排样方式。图8-11a、b为单排排样，图8-11c、d为双排排样，图8-11b、d为旋转180°的排样。

图8-11 常用的排样方式

排样在数学上是非线性规划问题，其目标函数为材料利用率。

对于卷料冲裁的情况，可以用步进材料利用率来评价排样方案的优劣。步进材料利用率用下式计算，

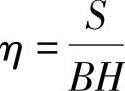
式中 S——一个步距上所排列的零件的面积；

B——卷料的宽度；

H——进给步距。

对于条料冲裁的情形，材料利用率为

式中 S₁——一个零件的面积；

n——条料上的零件个数；

B、L——条料的宽度和长度。

对于整块板料，材料利用率为

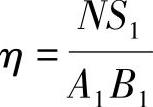
式中 N——由板料冲得的零件数目；(www.xing528.com)

A₁、B₁——板料的长度和宽度。

一般来说，排样可由图8-12中所示的两个参数φ和λ决定。

参数φ和λ的变化范围为

G{0≤φ≤π，-β（φ）≤λ≤β（φ）}

式中 β（φ）——φ的单值函数，它反映了图形在OY轴方向上的宽度与φ角的关系。

在一般情况下，排样的优化问题在于寻找φ和λ的最佳值，使目标函数

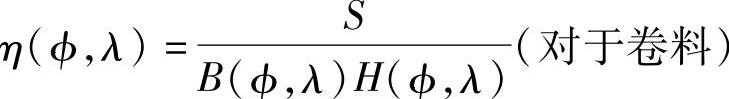
或者

在域G内达到最大值。

由于产品零件的复杂性，难以用一个统一的解析式表达排样问题的目标函数。所以，计算机辅助排样的方法虽有多种，但基本思想却是相同的，即从排列零件的所有可能的方案中选出最优者，也就是采用优化设计中的网格法解决毛坯排样问题。

图8-12 决定排样的参数

计算机排样方法可分为半自动化和自动化两大类。属于前者的方法需要较多的人机交互作用，利用图形交互设备和图形软件提供的操作功能在屏幕上完成图形布置，利用计算机比较材料利用率的大小，从中选择理想的方案。

自动化排样方法则由程序自动完成排样方案的产生、材料利用率的比较和最优方案的选择。常用的程序排样方法有多种，这里主要介绍多边形法和高度函数法。