隧道洞外平面控制和高程控制测量完成后,即可求得洞口控制点(各洞口至少有两个)的坐标和高程,同时,按设计要求计算洞内设计中线点的设计坐标和高程。按坐标反算方法计算出洞内设计点位与洞口控制点之间的距离、角度和高差关系(测设数据),测设洞内的设计点位,据此进行隧道施工,称为“洞口联系测量”。用竖井或沉井进行地下工程施工的,通过井口和井底进行联系测量的称为“竖井联系测量”。
1.隧道洞口联系测量
(1)掘进方向测设数据计算。图9-51(a)所示为一直线隧道的平面控制网,A、B、C、…、G为地面平面控制点。其中A、B 为洞口点,S1、S2 为A 点洞口进洞后的隧道中线第一个和第二个里程桩。为了求得A 点洞口隧道中线掘进方向及掘进后测设中线里程桩S1,计算下列极坐标法测设数据:
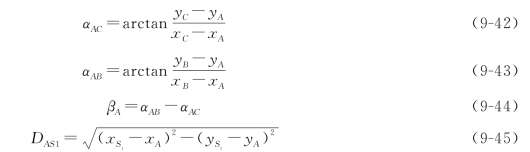
对于B 点洞口的掘进测设数据,可以作类似的计算。对于中间具有曲线的隧道,如图9-51(b)所示,隧道中线交点JD的坐标和曲线半径R 已由设计所指定,因此,可以计算出测设两端进洞口隧道中线的方向和里程。掘进达到曲线段的里程以后,可以按照测设道路圆曲线的方法测设曲线上的里程桩。
(2)洞口掘进方向标定。隧道贯通的横向误差主要由测设隧道中线方向的精度所决定,而进洞时的初始方向尤为重要。因此,在隧道洞口,要埋设若干个固定点,将中线方向标定于地面上,作为开始掘进及以后洞内控制点联测的依据。如图9-52所示,用1、2、3、4号桩标定掘进方向,再在洞口点A 和中线垂直方向上埋设5、6、7、8号桩作为校核。所有固定点应埋设在施工中不易受破坏的地方,并测定A 点至2、3、6、7号点的平距。这样,在施工过程中,可以随时检查或恢复洞口控制点A 的位置、进洞中线的方向和里程。

图9-52 山区隧道洞口掘进方向的标定
(3)洞内施工点位高程测设。对于平洞,应根据洞口水准点用一般水准测量方法,测设洞内施工点位的高程;对于深洞,则采用深基坑传递高程的方法(见“8.2.3已知高程点的测设”),测设洞内施工点的高程。
2.竖井联系测量
在隧道施工中,可以用开挖竖井的方法来增加工作面,将整个隧道分成若干段,实行分段开挖。例如,城市地下铁道的建造,每个地下车站是一个大型竖井,在站与站之间用盾构进行掘进,施工可以不受城市地面密集建筑物和繁忙交通的影响。
为了保证地下各开挖面能准确贯通,必须将地面控制网中的点位坐标、方位角和高程经过竖井传递到地下,建立地面和井下统一的工程控制网坐标系统,这项工作称为“竖井联系测量”。
竖井施工时,根据地面控制点将竖井的设计位置测设于地面。竖井向地下开挖后,其平面位置用悬挂大垂球或用垂准仪测设铅垂线,将地面的控制点垂直向下投影至地下施工面。其工作原理和方法与高层建筑的平面控制点垂直向上投影完全相同。高程控制点的高程传递可以用钢卷尺垂直丈量法或全站仪天顶测距法(见“8.4.9高层建筑施工测量”)。
竖井施工到达底面以后,应将地面控制点的坐标、高程和方位角作最后的精确传递,以便能在竖井的底层确定隧道的开挖方向和里程。由于竖井的井口直径(圆形竖井)或宽度(矩形竖井)有限,故用于传递方位的两根铅垂线的距离相对较短(一般仅为3~5m),垂直投影的点位误差会严重影响井下方位定向的精度。如图9-53所示,V1、V2 是圆筒形竖井井口的两个投影点,垂直投影至井下。由于投影点误差,至井底偏移到V′1、V′2。设V1V′1=V2V′2,则对投影边的方位角产生的角度误差为

设V1V2=5m,V1V′1=V2V′2=1mm,则产生的方位角误差Δα=1′12″。一般要求投影点误差应小于0.5mm。两垂直投影点的距离越大,则投影边的方位角误差越小。该边的方位角要作为地下洞内导线的起始方位角,因此,在竖井联系测量工作中,方位角传递(定向)是一项关键性工作。竖井联系测量主要有“一井定向”“两井定向”等方法。
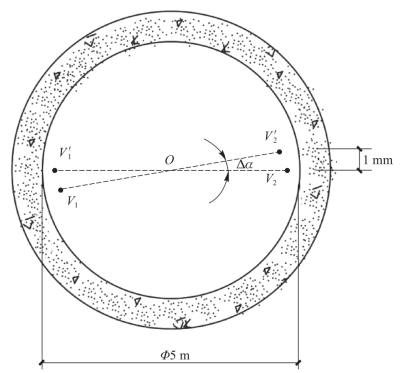
图9-53 竖井方位角传递误差
(1)一井定向。通过一个竖井口,用垂线投影法将地面控制点的坐标和方位角传递至井下隧道施工面,称为“一井定向”,如图9-54所示。在竖井口的井架上设V1 和V2 两个投影点,向井下投影的方法可以用垂球线法或用垂准仪法。下面介绍用高精度的垂准仪进行“一井定向”以传递坐标和方位角的方法。在竖井上方的井架上V1 和V2 两个投影点上架设垂准仪,分别向井底V1 和V2 两个可以微动的投影点进行垂直投影。
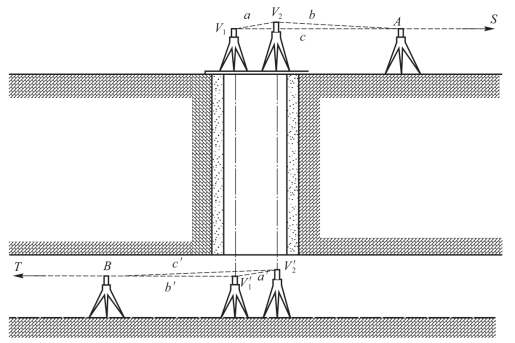
图9-54 一井定向联系测量
进行联系测量时,如图9-54、图9-55所示,在井口地面平面控制点A 上安置全站仪,瞄准另一平面控制点S 及投影点V1 和V2,观测水平方向,测定水平角ω 和α,同时测定井上联系△AV1V2 的三边长度a、b和c。同时,在井下隧道口的洞内导线点B 上也安置全站仪,瞄准另一洞内导线点T 和投影点V′1和V′2,测定水平角ω′、α′和井下联系ΔBV′1V′2中的三边长度a′、b′和c′。联系三角形应布置成直伸形状,α和α′角应为很小的角度(<3°),b/a 的比值应大于1.5,即a应尽可能大,这样有利于提高传递方位角的精度。
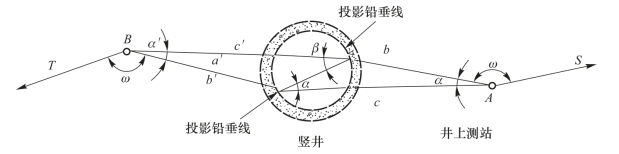
图9-55 一井定向的联系三角形
经过井上、井下联系三角形(图9-55)的解算,将地面控制点的坐标和方位角通过投影点V1和V2 传递至井下的洞内导线点。联系三角形的解算方法如下:
1)井上联系三角形解算。
①根据地面控制点A 和S 的坐标,反算AS 的方位角:
![]()
②根据测得的水平角α和ω,推算b边和c 边的方位角:
![]()
③根据b边和c 边的边长及方位角,由A 点坐标推算V1 和V2 点坐标(x1,y1)和(x2,y2):

④计算得的V1 和V2 点坐标应与测量而得到的边长a按下式作检核:
![]()
⑤根据V1 和V2 点的坐标,反算投影边V1V2 的方位角:(https://www.xing528.com)
![]()
2)井下联系三角形解算。
①根据井下观测的水平角α′和边长a′、b′,用正弦定律计算水平角β:

②根据投影边方位角α1,2和β角,推算c′边的方位角:
![]()
③根据C′边的边长及方位角,由V2 点坐标推算洞内导线点B 的坐标:

④根据井下观测的水平角α′和ω′,推算第一条洞内导线边的方位角:
![]()
洞内导线取得起始点B 的坐标和起始边B-T 的方位角以后,即可向隧道开挖方向延伸,测设隧道中线点位。
(2)两井定向。在隧道施工时,为了通风和出土方便,往往在竖井附近增加一通风井或出土井。此时,井上和井下的联系测量可以采用“两井定向”的方法,以克服因“一井定向”时两个投影点相距过进而影响方位角传递精度的缺点。
“两井定向”是在两个竖井中分别测设一根铅垂线(用垂准仪投影或挂大垂球),由于两垂线间的距离大大增加,因而减小了投影点误差对井下方位角推算的影响,有利于提高洞内导线的精度。
“两井定向”时,地面上采用导线测量方法测定两投影点的坐标。在井下,利用两竖井之间的贯通巷道,在两垂直投影点之间布设无定向导线(见“5.3.5导线测量的内业计算”),以计算得到连接两投影点之间的方位角和计算井下导线点的坐标。采用“两井定向”时的井上和井下联系测量控制网布设图形,如图9-56所示,A、B、C 为地面控制点,其中A、B 为近井点(靠近井口的控制点),V1、V2 为两个竖井中的垂直投影点,V1、E、F、V2 组成井下无定向导线。通过无定向导线的计算,得到井下控制点V1、E、F、V2 的坐标。
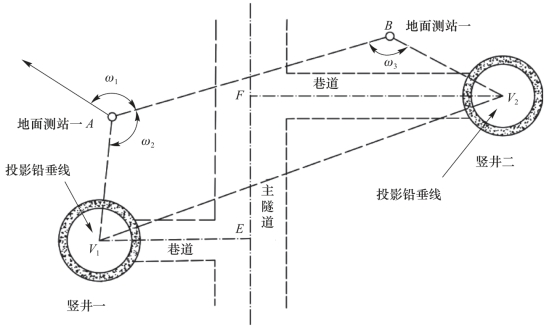
图9-56 “两井定向”联系测量
(3)陀螺仪测定井下方位角。在经纬仪或全站仪的支架上方安装陀螺仪,组成陀螺经纬仪或陀螺全站仪。图9-57(a)所示为全站仪上安装陀螺仪,图9-57(b)所示为陀螺仪目镜中的读数和“逆转点法”读数示意。陀螺仪定正北方向的原理:当陀螺仪中自由悬挂的转子在陀螺马达的驱动下高速旋转(约21500r/min)时,因受地球自转影响而产生一个力矩,使转子的轴指向通过测站的子午线方向,即真北方向。经纬仪或全站仪的水平度盘可根据真北方向进行定向(读盘读数设置为零度)。当经纬仪转向任一目标时,水平度盘的读数即测站至目标的真方位角。
真方位角与坐标方位角之间还存在一个子午线收敛角的差别,通过地面控制点和井下的联系测量,可以计算得到测站的子午线收敛角,从而将真方位角化为坐标方位角。
用陀螺经纬仪或陀螺全站仪测定方位角时,安置仪器于测站上,将望远镜大致瞄准正北方向,水平微动螺旋制动于中间位置。启动陀螺仪(启动指示灯亮),当陀螺转速达到规定值后(启动指示灯灭),缓慢旋松陀螺紧锁螺旋,使其放下陀螺灵敏部;高速旋转中的陀螺轴向通过测站的子午线两侧做衰减往返摆动,通过陀螺仪目镜可以看到指标线的左右摆动。连续跟踪和读取摆动中的指标线到达左、右逆转点时的水平方向值u1,u2,u3,…,根据三个连续方向值ui,ui+1,ui+2,按下式计算摆动中心点的方向值读数Ni(i=1,2,3,…):
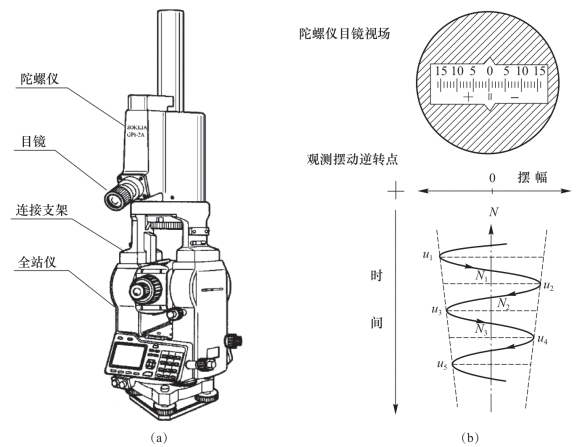
图9-57 陀螺仪定向观测

取各个Ni 的平均值,得到测站的真北方向的水平方向值。
用陀螺经纬仪或陀螺全站仪作地面和井下的联系测量时(图9-58),在井口的地面控制点A(近井点)安置陀螺经纬仪或陀螺全站仪,分别瞄准另一地面控制点S 和垂线投影点V(垂线钢丝如图9-58中所示或垂准仪投影时的觇牌),观测水平角和距离,推算AV 方向的坐标方位角αAV和V 点的坐标(xV,yV)。开动陀螺仪,测定AV 方向的真方位角AAV,按下式计算近井点A 的子午线收敛角:
![]()
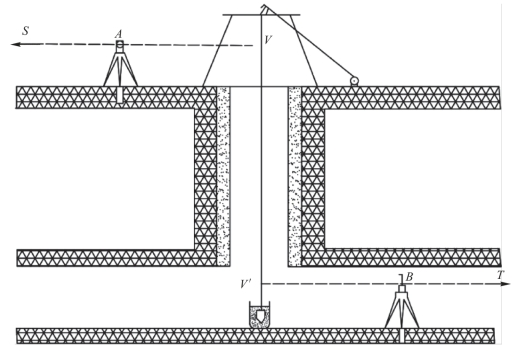
图9-58 用陀螺仪测定方位角
安置仪器于洞内导线点B,瞄准铅垂线V′和洞内另一导线点T,进行和地面点A 同样的观测;根据陀螺仪测定的真方位角ABV,计算洞内导线边BV 的坐标方位角:
![]()
根据投影点V 的坐标和BV 边的边长和坐标方位角,计算B 点的坐标;根据B 点观测的水平角,计算BT 边的坐标方位角。以此作为洞内导线的起始数据。
(4)竖井高程传递。竖井高程传递是根据井口地面水准点A 的高程,测定井下水准点B 的高程,如图9-59所示。在A 和B 点上立水准尺,竖井中悬挂钢卷尺(零点在下),井上、井下各安置一台水准仪,地面水准仪在水准尺和钢尺上的读数分别为a1 和b1,井下水准仪在钢尺和水准尺上的读数分别为a2 和b2,则B 点的高程为
![]()
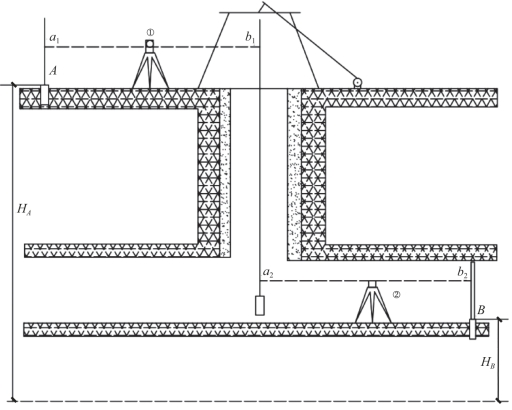
图9-59 竖井高程传递
竖井高程传递也可以采用全站仪天顶测距法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




