导线测量内业计算建议：简明易懂、信息准确

导线测量的内业计算目的就是根据已知的起始数据和外业观测成果，计算出各导线点的平面坐标。

在计算之前，首先要对外业成果进行全面检查和整理，应检查外业观测数据有无遗漏、记错、算错，是否符合精度要求，已知数据是否正确无误等。然后绘制出导线计算略图，并将导线观测角值、边长、已知数据注于图上相应位置。

1.闭合导线的计算

图5-14所示为一图根闭合导线，它必须满足多边形内角和条件及坐标条件，即从起算点开始，逐点推算各待定导线点的坐标，最后推回起算点，由于是同一点，故推算点坐标应等于该点的已知坐标。闭合导线的计算步骤如下：

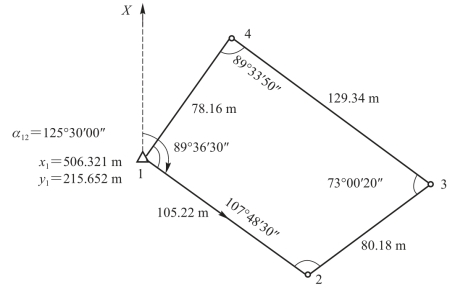
图5-14　闭合导线

（1）角度闭合差的计算与调整。闭合导线在几何上是一个多边形，其内角和的理论值为

式中　∑β理——多边形内角和的理论值；

　　　n——闭合导线内角个数。

在实际观测中，由于误差的存在，使实测的内角和∑β测与内角和理论值∑β理不相等，它们之间的差值称为角度闭合差，用fβ 表示，即

图5-14所示的闭合导线内角和闭合差为

角度闭合差的大小可反映出测角精度。不同等级的闭合导线均对方位角闭合差有具体的精度要求，可查阅《工程测量规范》（GB50026—2007）相应等级的导线测量技术规范。设其容许值为fβ容。若│fβ│＞│fβ容│，则认为角度观测成果不符合精度要求，应查找原因，如果计算无误，应去野外检测或重测。若│fβ│≤│fβ容│，则认为角度观测成果符合要求，可对观测角度加上改正数，以消除闭合差。本例闭合导线角度闭合差允许值说明fβ 不超过fβ容，成果合格，可以进行角度闭合差分配。

由于导线的转折角都是等精度观测，故角度闭合差的分配原则：将角度闭合差fβ 以相反符号平均分配在各观测角中，不能均分时可将余数凑整依次分配在相邻边较短的角度上，使改正后的角度之和等于理论值。分配闭合差的计算公式为

角度改正数vβ 计算正确与否，可用下式检核：

各转折角调整以后的值即改正后的各角值：

（2）推算导线边的坐标方位角。将起算边的已知方位角及改正后的角值代入方位角推算公式，便可推算出导线各边的坐标方位角。为了确保计算的正确性，最后必须再推回到1～2边，以进行检核。

（3）计算坐标增量、坐标增量闭合差、评定精度与分配闭合差。根据计算出的导线边坐标方位角及各边观测边长，按坐标正算计算每边的坐标增量。

对于闭合导线而言，导线的纵、横坐标增量之和，理论上应该等于零，即

但由于边长测量误差和角度误差闭合差调整后的残余误差使∑Δx测、∑Δy测不等于零，而产生坐标增量闭合差，分别用fx、fy 表示，即

将式（5-5）代入式（5-6）得

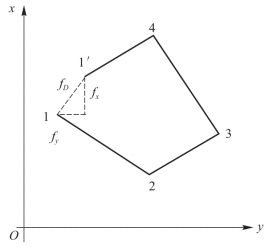
图5-15　导线全长闭合差

由于fx、fy 的存在，使得最终计算点1′和起始点1不重合，而产生了一段距离1－1′，如图5-15所示。这段距离称为导线全长闭合差，用fD 表示。按几何关系得

导线全长闭合差fD 值的大小从一个方面反映了导线测量精度，但由于导线误差的大小与导线长度相关，因此导线的精度是用相对闭合差来衡量的，即

表5-5、表5-6中对不同等级导线测量的相对闭合差限值作出规定。若相对闭合差大于表中所列限值，则观测成果不合格，应对外业记录和计算做全面检查，若未发现计算错误，则应到现场检查或重测。若相对闭合差小于或等于表中所列限值，则导线测量成果符合要求，可对坐标增量闭合差进行分配。

坐标增量闭合差分配方法是将fx、fy 反符号，按与边长成正比的原则，分配到各边的坐标增量中。以vΔxi－j、vΔyi－j 分别表示第i点至第j点导线边（第i边）的纵、横坐标增量的改正数，则(www.xing528.com)

因凑整而残留微小的不符值，可将其分配在长边的坐标增量上。坐标增量的改正数计算的正确性可用下列关系检核：

改正后的坐标增量为

（4）计算各导线点的坐标。根据起始点已知坐标及改正后的坐标增量，按下式依次推算到终点的坐标：

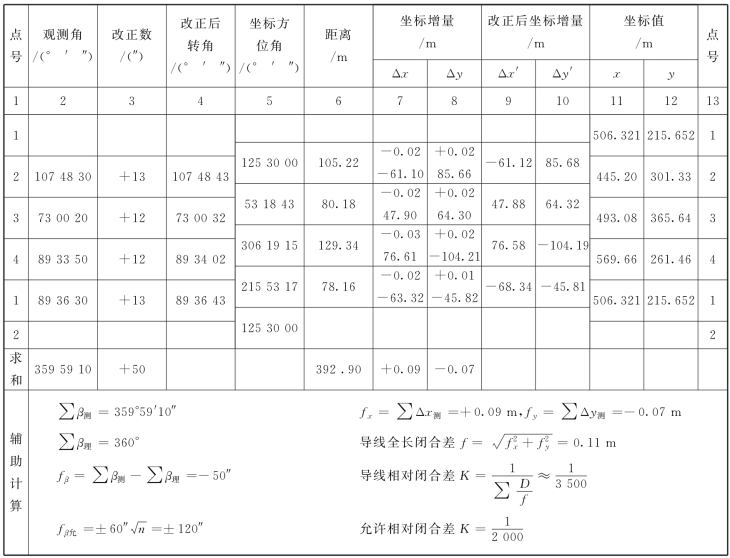
用式（5-13）最后推算出起始点的坐标，推算值应与已知值完全一致，以此检核整个计算过程是否有错。闭合导线形式（图5-14）的计算实例见表5-7。需要注意的是，最后坐标要一直推算到终点坐标为止，以作校核。示例1也展示了闭合导线计算过程。

表5-7　闭合导线坐标计算表

2.附合导线的计算

附合导线的内业计算步骤与闭合导线的内业计算步骤基本相同，但由于两者布设形式不同，所以在导线的角度闭合差与坐标增量闭合差的计算方面也有所不同。示例2为附合导线计算。下面主要介绍两者的不同之处。

【示例1】闭合导线计算（课件例题）原始数据见表5-8，其中灰色背景数据为已知。

表5-8　闭合导线计算表

注：Exbel中将角度（°）转化成（°′″）函数的方法：Exbel输入小数的“度”数，可以用时间的表示方法表示为“度分秒”=XY/24，设置为自定义格式：[h]°mm′ss″；“度分秒”转化成小数的度数时则乘以24。XY———某个单元格。

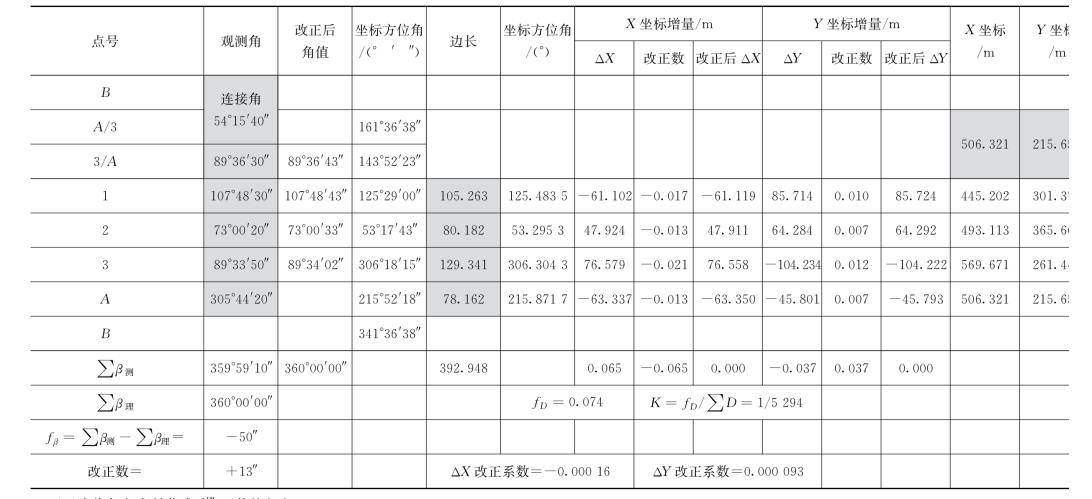
【示例2】附合导线计算原始数据见表5-9，其中灰色背景数据为已知。

表5-9　附合导线计算表

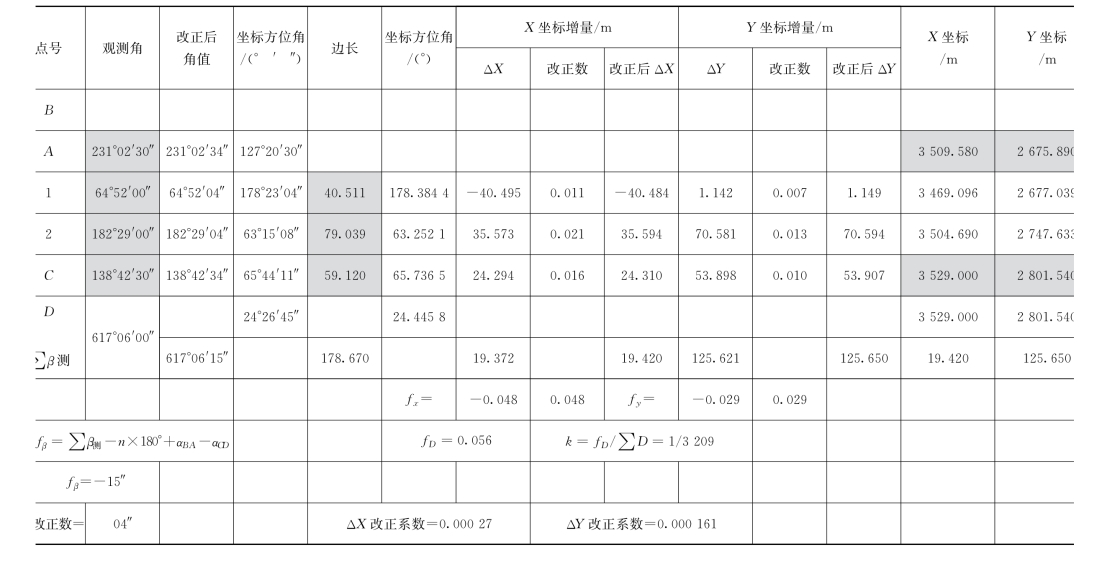
（1）角度闭合差的计算。附合导线首尾各有一条已知坐标方位角的边，如图5-16中的AB 边和CD 边，称为始边和终边。根据方位角推算公式可推算出各边的坐标方位角。这样，导线终边CD 边就有一个已知的坐标方位角α终和一个由观测角推算的坐标方位角α′终。由于测角误差的存在，导致α′终与α终之间存在差值，此差值即附合导线的角度闭合差，用fβ 表示，则有

如果角度闭合差fβ 不超过表5-5、表5-6中规定的容许值，则可将fβ 反号平均分配到各观测角中[见式（5-3）]，从而求得改正后的角值。

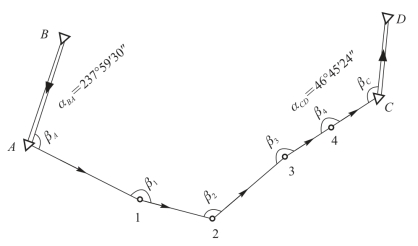
图5-16　附合导线

（2）坐标增量闭合差的计算。附合导线纵横坐标增量的总和，理论上应该等于终点坐标与起点坐标之差，即

由于边长误差及改正后角度剩余误差的影响，∑Δx测、∑Δy测与理论值往往不等，其差值即坐标增量闭合差fx、fy，即

将式（5-14）代入式（5-15），有

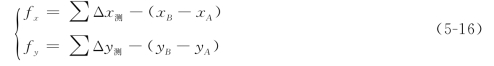
式中　xA、yA、xB、yB——导线起点、终点的已知坐标。

附合导线全长相对闭合差的计算，坐标增量闭合差的分配及最后的坐标推算与闭合导线相同。

3.支导线的坐标计算

支导线中没有检核条件，因此没有闭合差产生，导线转折角和计算的坐标增量均不需要进行改正，支导线的计算步骤如下：

（1）根据观测的转折角推算各边的坐标方位角。

（2）根据各边坐标方位角和边长计算坐标增量。

（3）根据各边的坐标增量推算各点的坐标。