计算坐标方向角方法总结

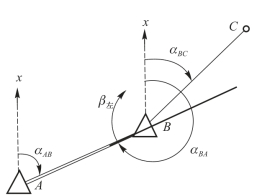
图4-22　推算坐标方位角

测量工作不仅需要测定点的坐标位置，还要测量直线的方向，一般采用坐标方位角表示。坐标方位角的测量，是从后面（后视）已知边的方位角开始，通过在测站点上所测的与后面点及前面点（前视）连线的转折角推算而得。

1.观测左角

如图4-22所示，已知直线AB，从A 点到B 点方向的坐标方位角为αAB，沿A、B、C 三点前进方向，在测站B点已测左侧转折角β左，则B 点前视BC 边的坐标方位角αBC如下推算：

式中，方位角αAB 在B 点后视方向，称为α后；αBC 在B 点的前视方向，称为α前；经推倒，无论α后、β左各自有多大，都有以下结论：

式（4-18）中180°之“±”的确定：

当α后＋β左≥180°时，取“－”号；

α后＋β左＜180°时，取“＋”号；

当α前＞360°时，则取“－360°”。

举例：α后=358°，β左=350°，则：

由于α前=528°＞360°，所以α前=α前－360°=168°。(www.xing528.com)

2.观测右角

当路线观测右角时，由于β右=360°－β左，即β左=360°－β右，代入式（4-18）则有：α前=α后＋（360°－β右）±180°，即

式中，±180°的符号及“－360°”的规则同观测左角；当α前＜0°时，则取“＋360°”。

3.通用公式

接上面叙述，综合考虑左右观测角，有通用公式：

课后讨论

1.简述三北方向的概念，以及其相互关系。

2.简述方位角、坐标方位角的概念。

3.简述正反方位角的概念及关系。

4.简述象限角的概念及其与坐标方位角的转换关系。

5.何谓坐标反算？其计算公式是什么？

6.画图说明坐标方位角推算公式。