视距测量原理详解

1.视线水平时的视距测量原理

如图4-10所示，A、B 为地面上两点，为测定两点之间的水平距离D 及高差h，在A 点安置仪器，B 点竖立视距标尺。由于望远镜视准轴水平，照准B 点标尺，视准轴与标尺垂直交于Q 点。若尺上M、N 两点成像在十字丝两根视距丝m、n 处，则标尺上MN 长度可由上下视距丝读数之差求得，上下视距丝读数的差称为尺间隔，用l表示。

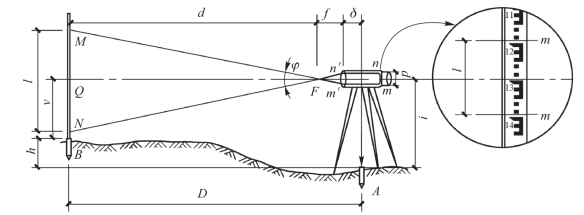
图4-10　视线水平时的视距测量

由Δm′n′F 与ΔMNF 相似得：

式中　l——尺间隔；

　　　f——物镜焦距；

　　　p——视距丝间隔。

由图4-10中可以看出：

式中　δ——物镜至仪器中心的距离。

令=K，K 为乘常数，f＋δ=C，C 为加常数，则

目前测量常用的内调焦望远镜，在设计制造时，已适当选择了组合焦距及其他有关参数，使视距常数K=100，C 接近于零。因此式（4-10）可写成：

由图4-10可以得出两点之间高差公式：

式中　i——仪器高；(www.xing528.com)

　　　v——觇标高，即望远镜十字丝中丝在标尺上的读数。

图4-11　视线倾斜时的视距测量

2.视线倾斜时的视距测量原理

如图4-11所示，在地面起伏较大地区进行视距测量，必须使视线倾斜才能在标尺上读数。这时视线不再垂直于视距尺，故不能直接用式（4-11）计算水平距离，如果将视距间隔MN换算成与视线垂直的视距间隔M′N′，就可用式（4-11）计算倾斜距离D′，再根据D′和竖直角α计算出水平距离D 及高差h，因此，解决问题的关键在于求出MN 与M′N′之间的关系。

从图4-11中可以看出：

式中的角值很小，只有17′11″，故可近似地认为∠MM′G 和∠NN′G 是直角。

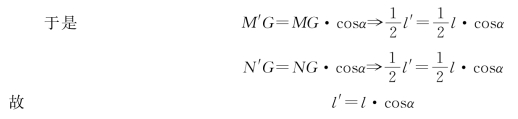
将其代入式（4-11）得：

所以A、B 两点之间的水平距离为

由图4-11中还可看出，A、B 两点之间的高差为

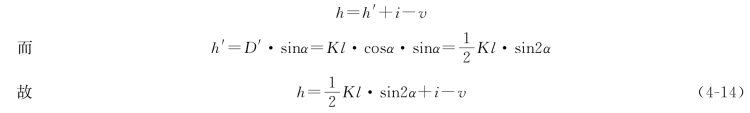
在实际工作中，一般尽可能使觇标高v等于仪器高i，这样可以简化高差h的计算。

式（4-13）和式（4-14）为视距测量计算的基本公式，当视线水平，竖直角α=0°时，即成为式（4-11）和式（4-12）。