如何减小观测误差？

1.仪器对中误差

在安置仪器时，由于对中不准确，使仪器中心与测站点不在同一铅垂线上，称为对中误差。如图3-25所示，A、B 为两个目标点，O 为测站点，O′为仪器中心，OO′的长度称为测站偏心距，用e表示，其方向与OA 之间的夹角θ 称为偏心角。β为正确角值，β′为观测角值，由对中误差引起的角度误差Δβ为

因δ1 和δ2 很小，故

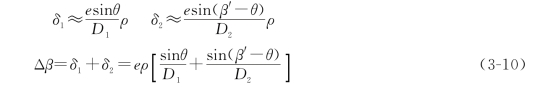
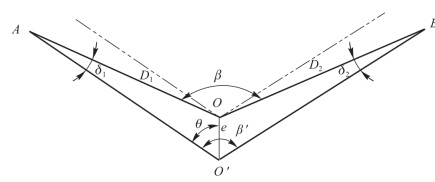
图3-25　仪器对中误差

分析式（3-10）可知，对中误差对水平角的影响有以下特点：

（1）Δβ与偏心距e 成正比，e越大，Δβ越大；

（2）Δβ与测站点到目标的距离D 成反比，距离越短，误差越大；

（3）Δβ与水平角β′和偏心角θ的大小有关，当β′=180°，θ=90°时，Δβ最大。

例如，当β′=180°，θ=90°，e=0.003m，D1=D2=100m 时

因为，对中误差引起的角度误差不能通过观测方法消除，所以，观测水平角时应仔细对中。当边长较短或两个目标与仪器接近在一条直线上时，要特别注意仪器的对中，避免引起较大的误差。一般规定对中误差不超过3mm。

(www.xing528.com)

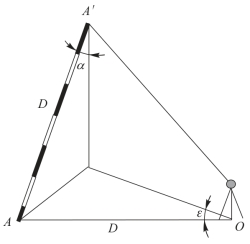
图3-26　目标偏心误差

2.目标偏心误差

水平角观测时，常用测钎、测杆或觇牌等立于目标点上作为观测标志。当观测标志倾斜或没有立在目标点的中心时，将产生目标偏心误差。如图3-26所示，O 为测站，A为地面目标点，AA′为测杆，测杆长度为L，倾斜角度为α，则目标偏心距e为

目标偏心对观测方向影响为

目标偏心误差对水平角观测的影响与偏心距e成正比，与距离成反比。为了减小目标偏心误差，瞄准测杆时测杆应立直，并尽可能瞄准测杆的底部。当目标较近又不能瞄准目标的底部时，可以采用悬吊垂线或选用专用觇牌作为目标。

3.整平误差

整平误差是指安置仪器时竖轴不竖直的误差。倾角越大，影响也越大。一般规定在观测过程中，水准管偏离零点不得超过一格。

4.瞄准误差

瞄准误差主要与人眼的分辨能力和望远镜的放大倍率有关，人眼分辨两点的最小视角一般为60″。设经纬仪望远镜的放大倍率为V，则用该仪器观测时，其瞄准误差为

一般DJ6 型光学经纬仪望远镜的放大倍率V 为25～30 倍，因此，瞄准误差mV 一般为2.0″～2.4″。

另外，瞄准误差与目标的大小、形状、颜色和大气的透明度等也有关，因此在观测中应尽量消除视差，选择适宜的照准标志，熟练操作仪器，掌握瞄准方法，并仔细瞄准以减小误差。

5.读数误差

读数误差主要取决于仪器的读数设备，同时，也与照明情况和观测者的经验有关。对于DJ6型光学经纬仪，用分微尺测微器读数，一般估读误差不超过分微尺最小分划的1/10，即不超过±6″，对于DJ2 型光学经纬仪一般不超过±1″。如果反光镜进光情况不佳、读数显微镜调焦不好，以及观测者的操作不熟练，则估读的误差可能会超过上述数值。因此，读数时必须仔细调节读数显微镜，使度盘与测微尺影像清晰，也要仔细调整反光镜，使影像亮度适中，再仔细读数。使用测微轮时，一定要使度盘分划线位于双指标线正中央。