测量误差：概念与特点

1.测量误差的概念

任何测量工作，由于各种因素的影响，测量所得的量值z并不准确地等于被测之量的真值A，二者之差称为测量误差。修正量与误差值大小相等、方向相反。对测得值加以修正即得到真值，即A=x＋C。由于测量误差不可避免，因而无法知道误差的准确值。人们只能估计在一定概率下可能达到的误差限，这样估计的误差限称为测量的不确定度。

2.测量误差的来源

（1）测量仪器和工具。测量工作需要用测量仪器进行，测量仪器尽管在不断地改进，但总是受到当前科学和生产水平的限制而只具有一定的精确度，因此，测量结果受其影响。另外，虽然仪器使用前进行了检校，但仪器的残差同样会或多或少地影响观测结果。

（2）观测者。由于观测者感觉器官鉴别能力的局限性所引起的误差。例如，在厘米分划的水准尺上，由观测者估读毫米数，则1mm 左右的读数误差是完全有可能的。另外，观测者的技术熟练程度也会给观测成果带来不同程度的影响。

（3）外界条件影响。测量工作进行时所处的外界环境中的空气温度、风力、日光照射、大气折光及烟雾等情况时刻在变化，也会使测量结果产生误差。

人、仪器和外界条件是引起测量误差的主要因素，通常称为观测条件。观测条件相同的各次观测，称为等精度观测；观测条件不相同的各次观测，称为非等精度观测。

在观测结果中，有时还会出现错误，称为粗差。粗差在观测结果中是不允许出现的，为了杜绝粗差，除认真作业外，还必须采取必要的检核措施。

3.测量误差的分类与偶然误差的特征

（1）测量误差的分类。测量误差可分为系统误差和随机误差两类。在相同的条件下进行多次重复测量，若每次测量的误差是恒定的，或者是按照一定规律而变化的，这类误差称为确定性误差或系统误差。产生系统误差的原因（误差源）一般是可以掌握的，系统误差的出现是有规律可循的。若在一组等精度测量中，每次测量的误差是无规律的，其值或大或小，或正或负，那么，这类误差就称为随机误差或偶然误差。任何测量误差的出现都必然有其原因和规律，但由于人们对复杂客观事物的认识有限，对于未能掌握的部分就只能归之于偶然。一旦掌握了某一部分随机误差的原因和规律，这一部分误差就成为一种系统误差；反之，某些误差，虽已掌握其原因和规律，但由于中间掺杂着某些难以控制的偶然因素，以致误差的具体数值也呈现出一定的随机性。成批生产的仪器的制造公差、测量过程中操作员对仪器的调谐和电子测量中的噪声影响等，就是典型的事例。这类误差也称为随机性系统误差或半系统误差，在测量实践中常被当作随机误差来处理。

（2）偶然误差的特征。偶然误差从表面上看没有任何规律性，但是随着对同一量观测次数的增加，大量的偶然误差就表现出一定的统计规律性。例如，对一个三角形的三个内角进行测量，三角形各内角之和l不等于其真值180°，用X 表示真值，则l与X 的差值Δ 称为真误差（即偶然误差），即

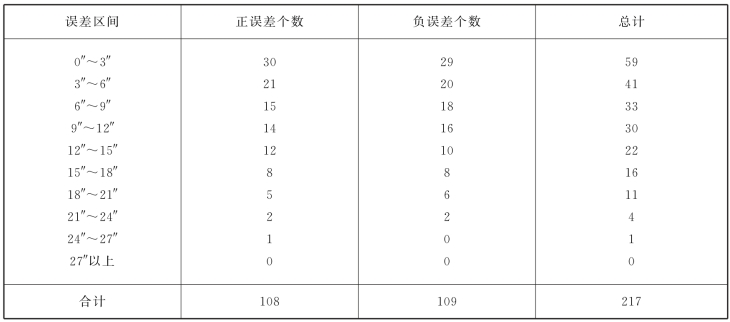
从表1-3中可知，现在相同的观测条件下观测了217个三角形，按式（1-14）计算出217个内角和观测值的真误差，再按绝对值大小，分区间统计相应的误差个数，并列入表中。从表1-3中可以看出：(www.xing528.com)

（1）绝对值较小的误差比绝对值较大的误差个数多。

（2）绝对值相等的正负误差的个数大致相等。

（3）最大误差不超过27″。

表1-3　偶然误差的统计

通过长期对大量测量数据分析和统计计算，人们总结出了偶然误差的四个特性：

（1）在一定观测条件下，偶然误差的绝对值有一定的限值，或者说，超出该限值的误差出现的概率为零。

（2）绝对值较小的误差比绝对值较大的误差出现的概率大。

（3）绝对值相等的正、负误差出现的概率相同。

（4）同一量的等精度观测，其偶然误差的算术平均值，随着观测次数n 的无限增大而趋于零，即

式中　[Δ]——偶然误差的代数和，[Δ]=Δ1＋Δ2＋…＋Δn。

上述第四个特性是由第三个特性导出的，说明偶然误差具有抵偿性。