本节学习要点
1.了解两种加工方法
2.学会螺纹参数的计算
3.消化例题中的程序
从本节开始,讲解的螺纹牙型已经不是某单条曲线了,而是多种曲线的组合。比如例6-9中要讲解的凸圆弧牙型螺纹。
从字面上看,凸圆弧牙型螺纹与之前所讲的凹圆弧牙型螺纹很类似,但事实果真如此吗?让我们看一幅示意图。例6-9图6-11 l
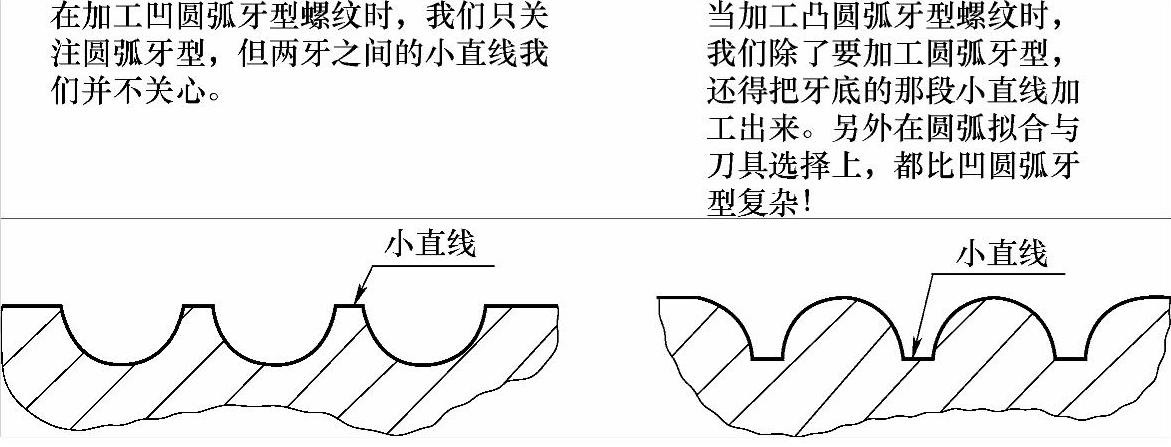
图 6-11
通过图6-11的描述,就不需要再过多地介绍这两种螺纹的区别。
那么接下来我们详细地分析凸圆弧牙型螺纹的加工思路。
首先,对刀具轨迹进行剖析。在正弦曲线螺纹这一节说过,加工螺纹其实就是拟合出整个牙型。在本例中,要拟合整个牙型有两种方法,如例6-10所示。
例6-10
方法1(见图6-12):
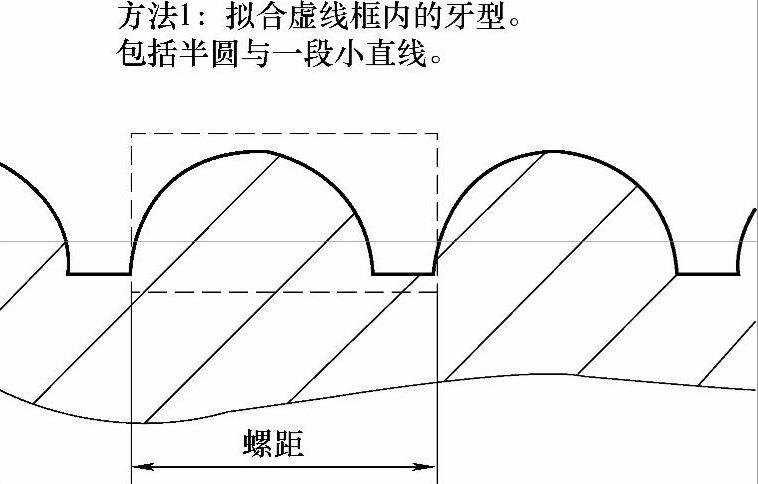
图 6-12
方法2(见图6-13)
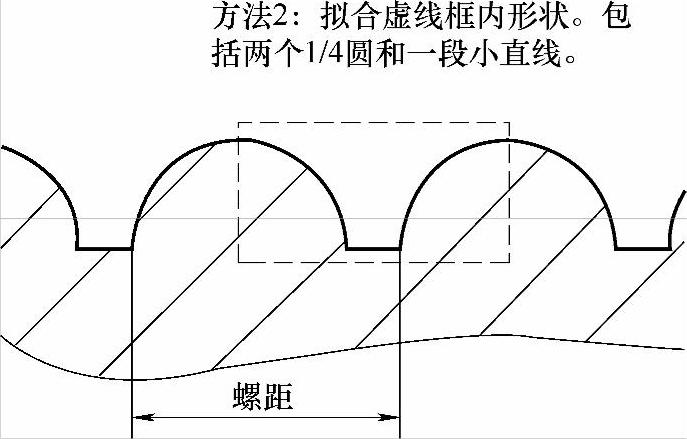
图 6-13
现在就两种方法进行分析。
这两种方法不管选择哪一种,刀具肯定选用切槽刀(定制刀具除外)。既然是切槽刀,那么采用方法1的话,需要在圆弧最高点处,移动一个槽刀刀宽利用右刀尖进行加工;而采用方法2加工时,则不需要考虑“移动刀宽”的问题,只要拟合两个1/4圆和底部的小直线即可。但这里作为讲解,还是把两种方法都详细解释并编制加工程序。
我们先来看方法1。
例6-11(图6-14)
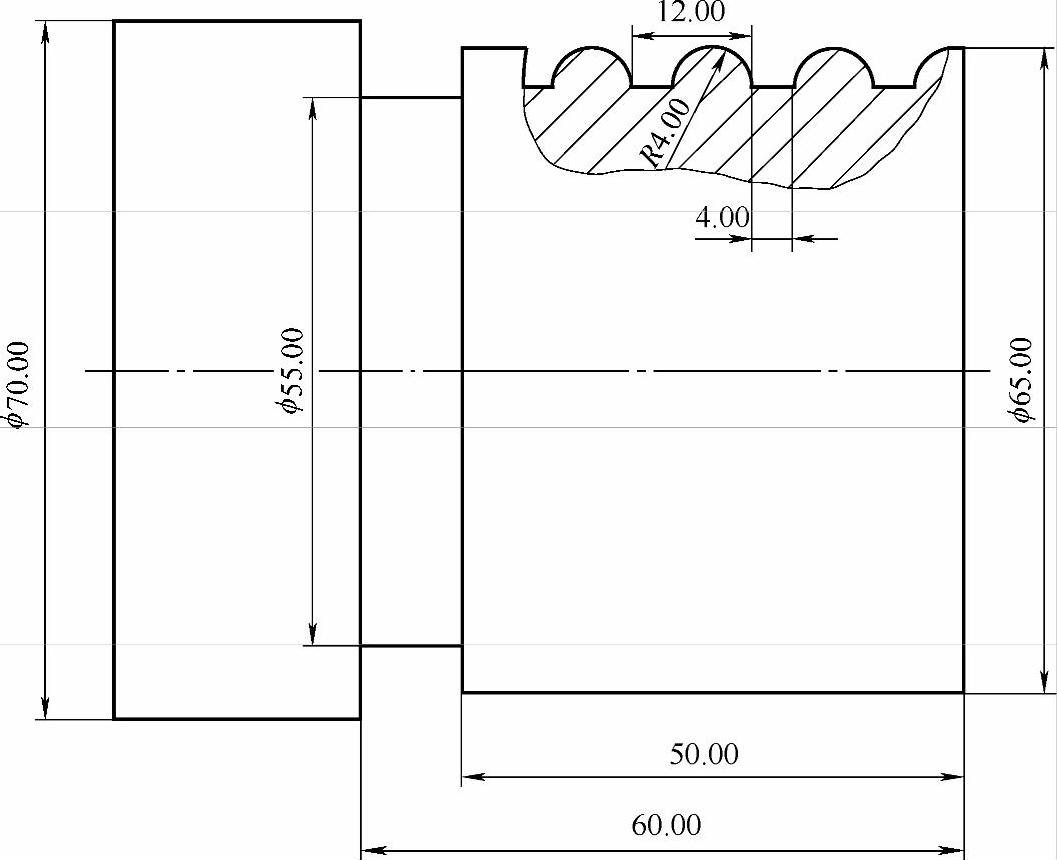
图 6-14
根据图6-14所示图样,选用刀宽为3mm的切槽刀。
在粗加工的时候虽然可以采用“先中间、后两边”方法,但是由于牙型两侧不对称,两边余量没法均分。所以总槽口宽度不能除以2。
在程序结构上,需要采用两个程序加工。第一个是加工小直线与右半边的圆弧,第二个程序是加工左半边的圆弧。这样一来整个牙型就出来了。中途要注意移动刀宽。
最后,假设把刀具放在小直线处。以这个点为基准,进行借刀车削加工,如例6-12所示。
例6-12(图6-15)
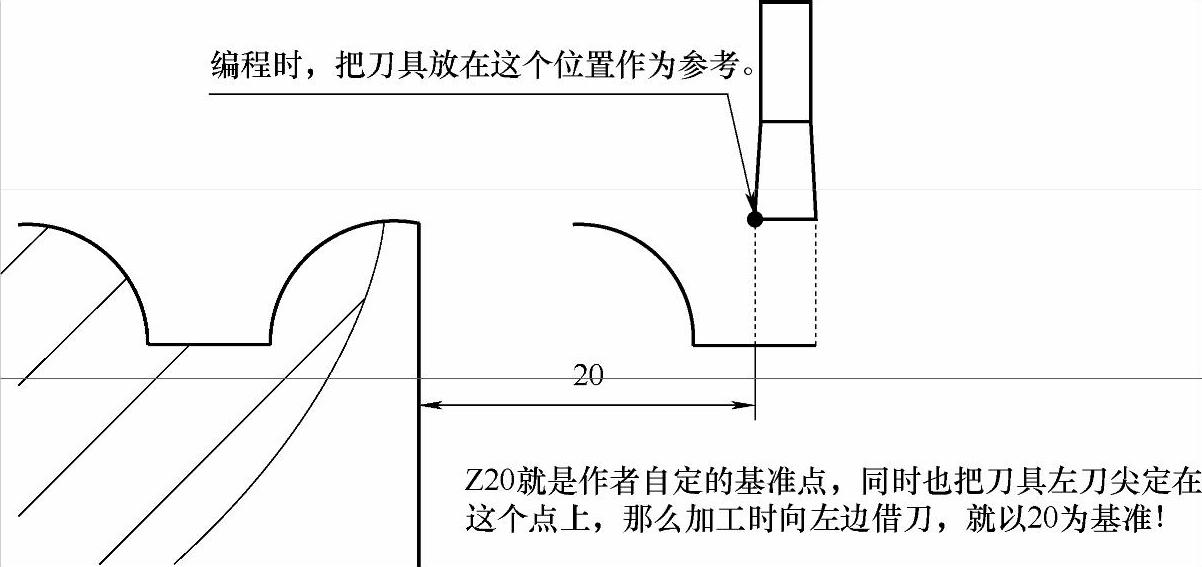
图 6-15
根据图6-15不难发现,在Z向借刀时,需要算出刀具当前所在深度所对应的槽口总宽。这个宽度怎么算,让我们通过图6-16说明。
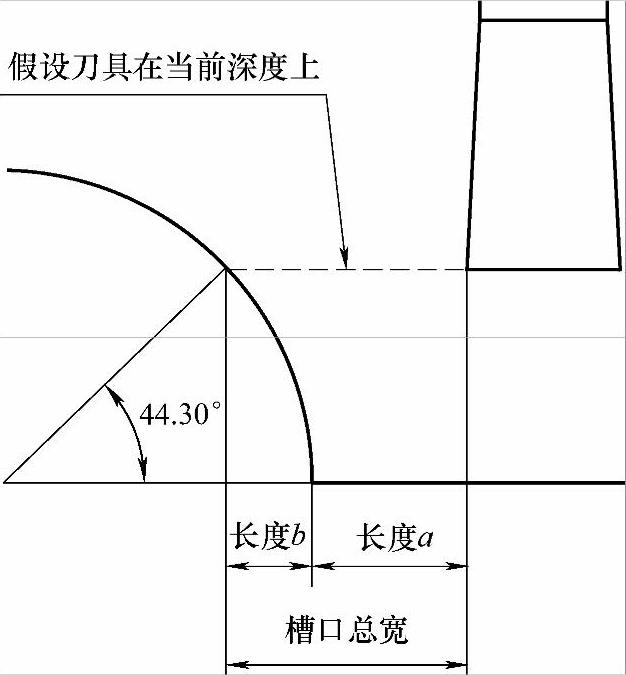
图 6-16
由图6-16可知,在当前深度上的槽口总宽就等于长度a加上长度b。长度a其实就是牙槽底宽减去刀具宽度;而长度b则用半径−半径×cos(44.30)即可。当槽口总宽算好后,只要设定一个变量向槽宽长度累加,若比当前槽宽小,说明没借完。下面就看看在程序中如何实现上面的想法。
例6-13

 (https://www.xing528.com)
(https://www.xing528.com)
当这个程序写完,其实只是加工了右半边的小圆弧和牙底的直线段。还剩下左半边的圆弧没加工。让我们先看看右侧加工的效果图。图6-17左图为粗加工过程,图6-17右图为精加工结束。

图 6-17
当右侧加工完毕,该加工左侧小圆弧了。
在加工右侧时,前面说过一定要注意刀宽的问题。那到底应该移多少距离呢?是不是移动一个刀宽就行了?请看示意图。
例6-14(图6-18)
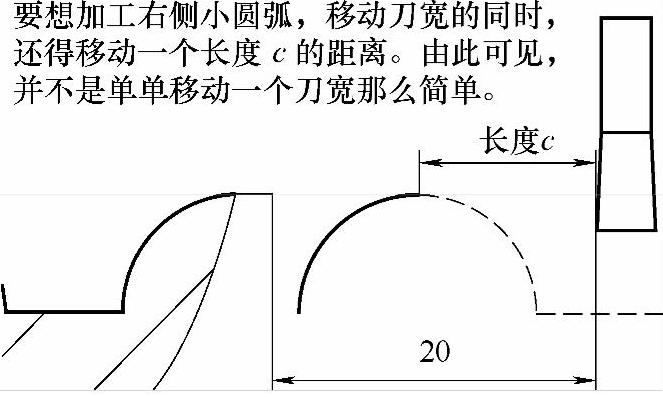
图 6-18
那么长度c怎么求呢?我们发现,长度c其实就是圆弧半径加上牙底宽度(减去刀宽)。那么根据图样可以求出长度c,即c=4+(4−3)=5。那么需要移动的总距离就是:5+3=8。因此在加工右侧小圆弧时,把基准点20改成12即可。下面就把整个程序写完。
例6-15


写到这,程序整个结束。让我们把两个程序一起仿真看看加工效果,如图6-19所示。
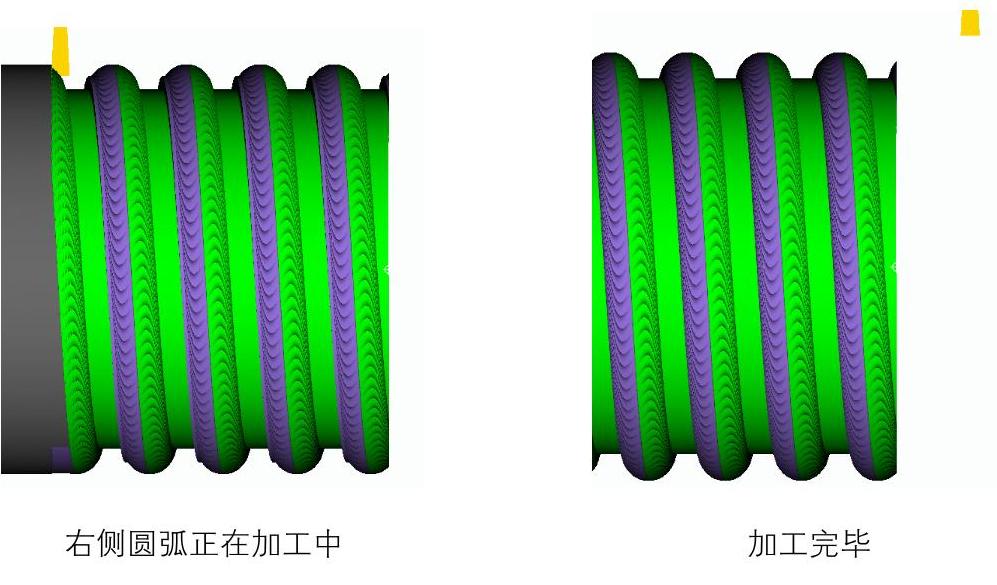
图 6-19
以上就是方法1的加工方法及思路。可以发现过程较复杂。对于新手来说单单“移动刀宽”这个概念可能也不太好理解。下面再介绍下方法2。学完之后读者就发现方法2明显比方法1简单得多。
讲解之前,让我们先看看方法2的加工示意图(见图6-20)。
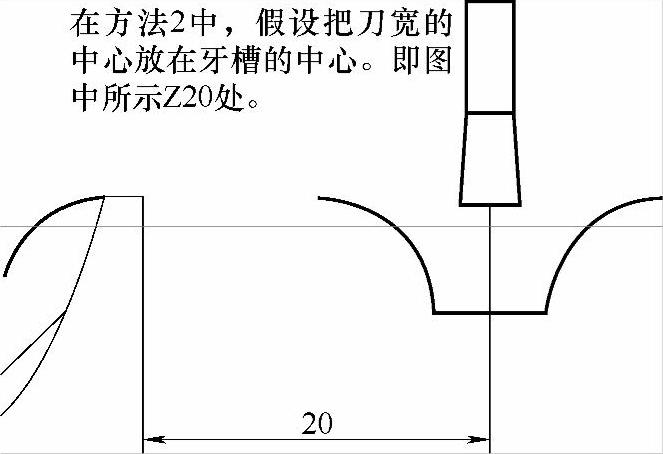
图 6-20
图6-20中有个概念我们要明白——对刀点。乍看之下,当对刀时(Z向)需要把槽刀刀宽中心作为Z零点。其实不需要!我们仍可以用左刀尖对刀,当程序中还是使用20为基点的时候,那么刀宽中心所在的位置就是21.5。但在左右借刀时,是把余量平均分的。也就是说牙型槽的中心也会跟着移到21.5。这一点我们不必太纠结。如果实在不明白,只要记住在Z向定位的时候,刀具距端面的长度,要大于槽宽的一半以上!
在方法2里,会发现要拟合的牙型是左右对称的。因此我们很快就能想到采用“先中间、后两边”加工方法。唯一要解决的问题就是求出当前深度下所对应的槽口宽度。还是利用示意图来解决这个问题。
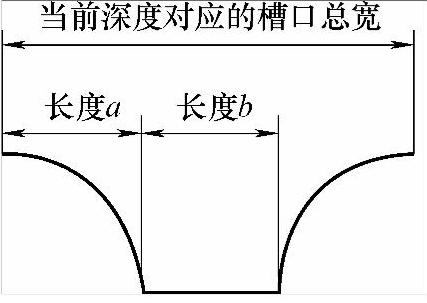
图 6-21
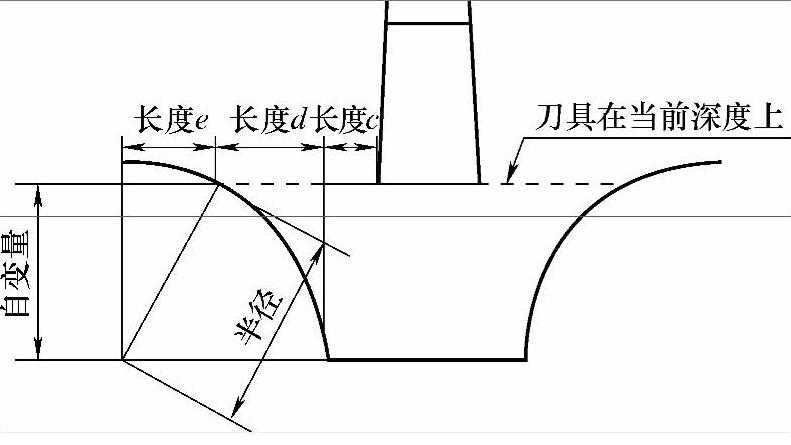
图 6-22
从图6-21中不难发现,当前深度所对应的槽宽其实就是长度a乘以2,再加上长度b。但切记要减去刀宽!而长度a的计算在方法1中介绍过,采用的是三角函数。但这里我再介绍另一种计算方法——勾股定理。
从图6-22中可以看到,只要算出长度d、长度c,就能把当前槽宽算出来。而长度c其实就是牙底宽减去刀宽,再除以2。但长度d呢?
我们发现,如果把长度e先求来,然后再用半径减去长度e,就能求得长度d了。而长度e又恰巧是直角三角形的一条直角边。根据勾股定理很快就能求得它的长度了。我们会在程序中实现这个计算方法。下面就正式编制加工程序。
例6-16


让我们看看图6-23所示的加工效果图。
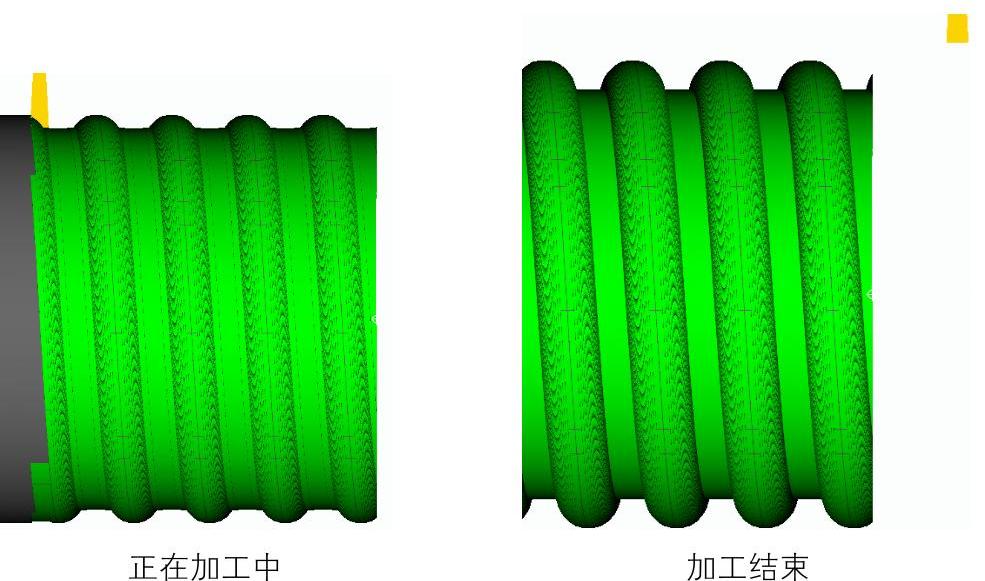
图 6-23
综合来说,本节内容较之以往难度颇大。但仔细梳理螺纹之间的数据关系其实并不复杂。所以在编制程序的时候,一旦确定了刀具轨迹,剩下的事就是寻找数据关系了!
本节到这就结束了。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




