本节学习要点
1.如何定位圆弧牙型上的点
2.掌握两种例题中的两种刀具轨迹编程方法
3.完全吸收例题程序的思路
圆弧牙型螺纹在滚珠丝杠中是比较常见的,另外在技能大赛里也很常见。所以本节内容将对该螺纹做详细讲解。
首先我们想想前面几节一直说到的一个问题:定位点。
要想车出某牙型,实际上就是在定位时,把该牙型上的每个点依次定位好,然后用G32依次车削过去。正如梯形螺纹那一节讲的,这个点该如何定位呢?让我们先看一个示意图(见图5-22)
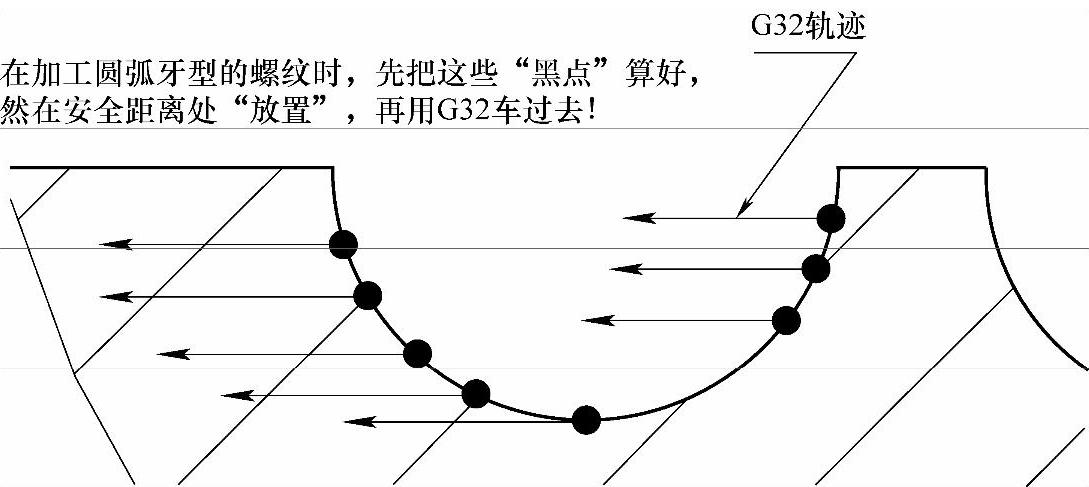
图 5-22
这些点要如何求?其实与梯形螺纹一样,也是通过三角函数求得的。但过程要比梯形螺纹稍微复杂些,我们还是通过一个示意图(见图5-23)来解决这个问题。
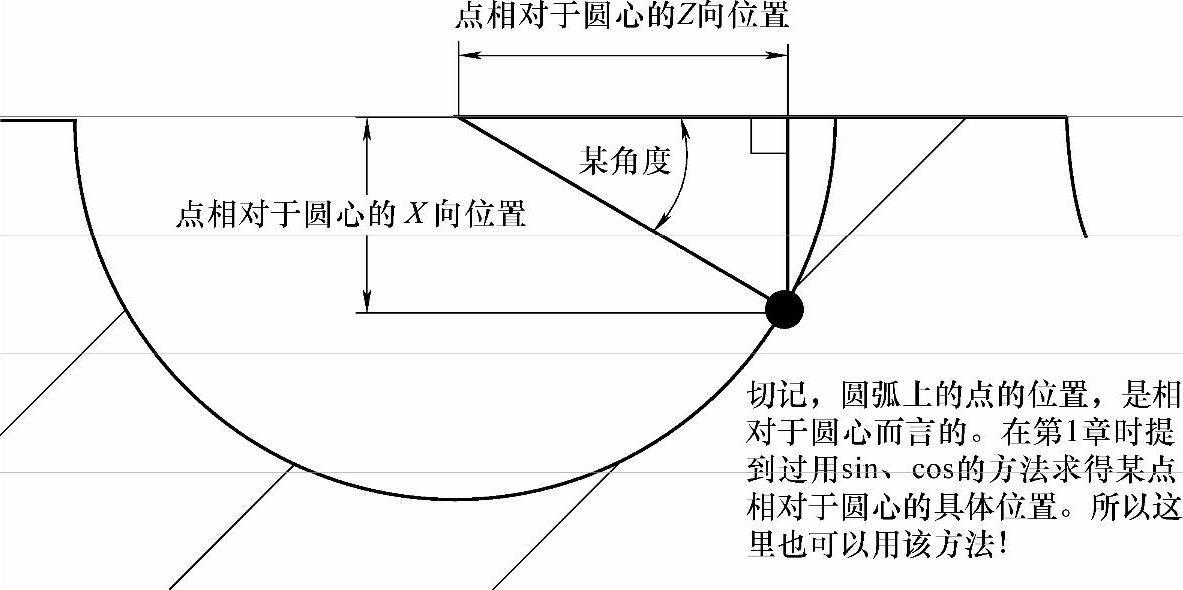
图 5-23
由图5-23可以得知,其角度是已知的量(编程时角度是个自变量)。想求得该点的X值时,可以根据sin(角度)=对边/斜边,推导出对边(即X向)=sin(角度)×斜边。而斜边恰好又是半径!所以X向很容易就被求出来了。同理,Z向就是cos(角度)=邻边/斜边,推导出邻边(即Z向)=cos(角度)×斜边(关于三角函数问题请参考第1章)。
接下来再谈谈另一个问题——角度正负号的判定!
有很多读者不知道角度的正负号是怎么判定的,一会正、一会负,易犯迷糊。其实它的判定很容易。以后置刀架为基准,如果角度是逆时针旋转即为正,顺时针旋转即为负!如图5-24所示。
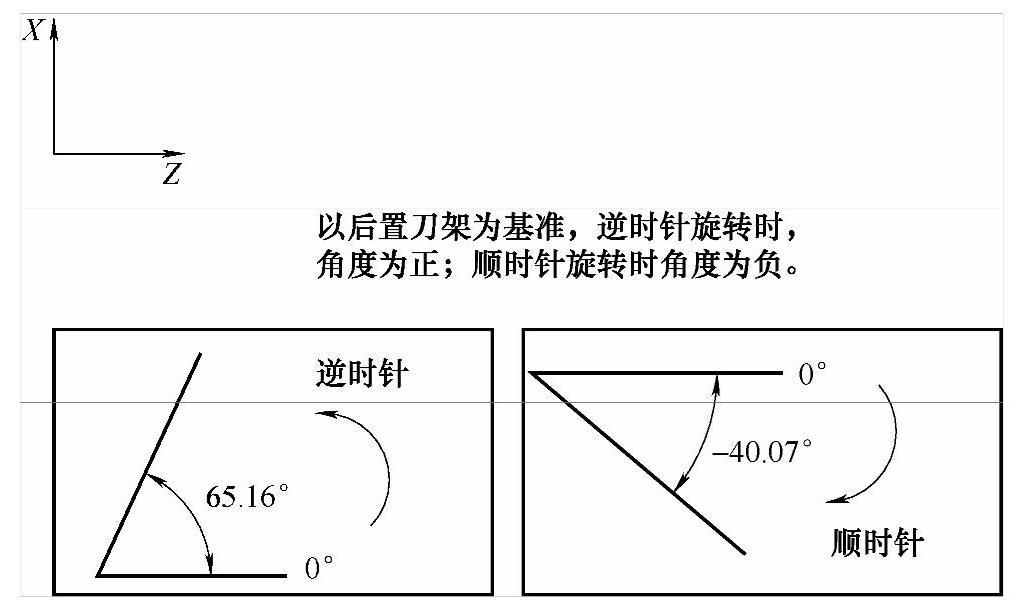
图 5-24
所以在图5-23中,它的圆弧是凹下去的,那以后置刀架为基准,顺时针方向变化即可,因此角度的变化范围是0°~−180°(即角度为负值)。
关于“点”怎么求,现在已经知道了,再来看看刀具的问题。
要加工这种螺纹,可以分粗、精两把刀,比如用切槽刀开粗,球刀精加工;也可以只用球刀粗精一起加工。本节先介绍切槽刀开粗法。
对于切槽刀粗加工时,需要注意的是干预点的问题,如图5-25所示。
如果直接理想化地加工到底,那做出来的螺纹底部将是直线,而非圆弧了。当然,除了圆弧车刀以外的刀具都会发生干预的问题,在加工时要注意这一点。当用切槽刀粗车好后,再用球刀精加工即可。下面先用切槽刀编制粗车程序!本书给读者提供两种加工方法供参考,还是那句话,你想怎么开粗就怎么写程序。
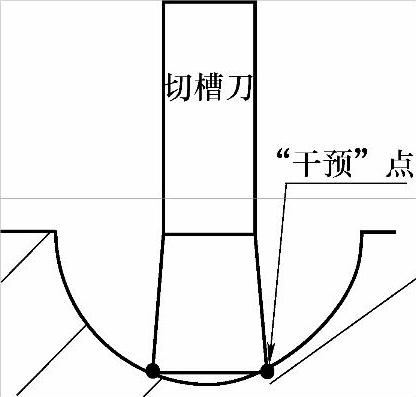
图 5-25
方法一:切槽刀粗车,球刀精车(切槽刀刀宽3mm、球刀半径R2mm)
例5-15(图5-26)
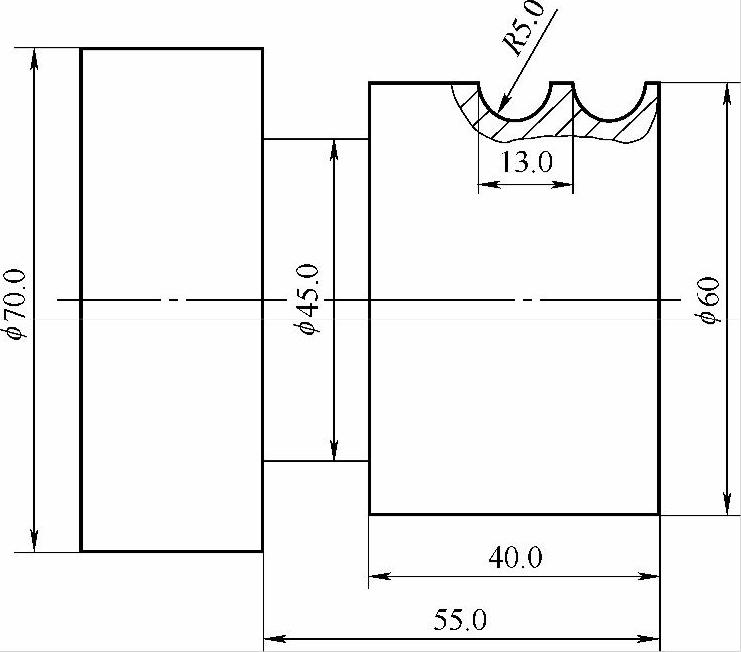
图 5-26
前面提到过干预点的问题。所以可以在软件中把这个干预点找出来,防止过切,如图5-27所示。
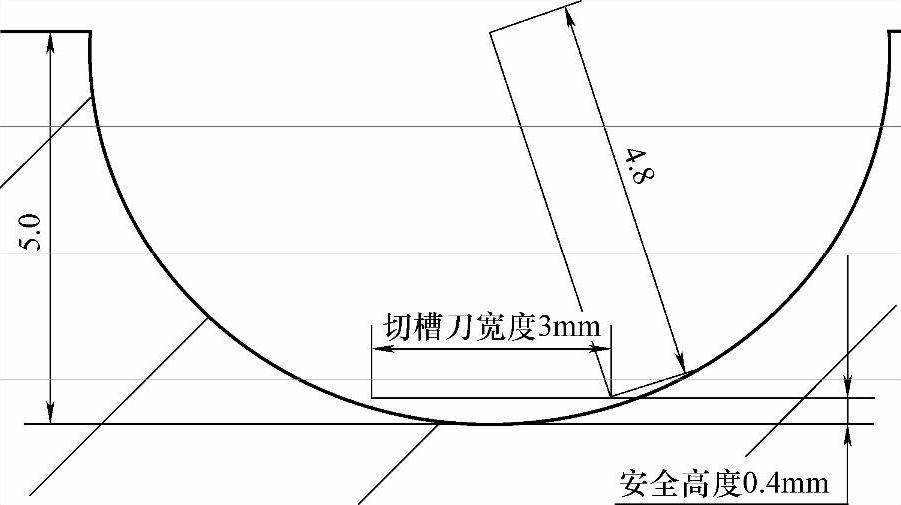
图 5-27
根据图5-27我们可以看出,当刀具宽度为3mm时,其X向最大切削深度为4.6mm(单边值,这个值是作者自定的),留出0.4mm的安全距离。同时在Z向也要留出余量,其实就是把半径缩小。那缩小到什么尺寸?能够正好把3mm刀宽交于弧上即可。所以由图5-27可知,缩小后的半径是4.8mm(实际测量值是4.838mm)。那么在实际车削的时候,以4.8mm为半径粗车即可。
最后该找找编程所需要的数据了。
由于在加工的时候,把切槽刀中心放在了圆心的位置(即刀具左、右两点相对圆心的坐标是−1.5、1.5),所以实际的Z向借刀距离要减去刀宽。这个问题和梯形螺纹是一个道理。但要借的总长是多少呢?该如何求?老规矩,直接上图(见图5-28)。
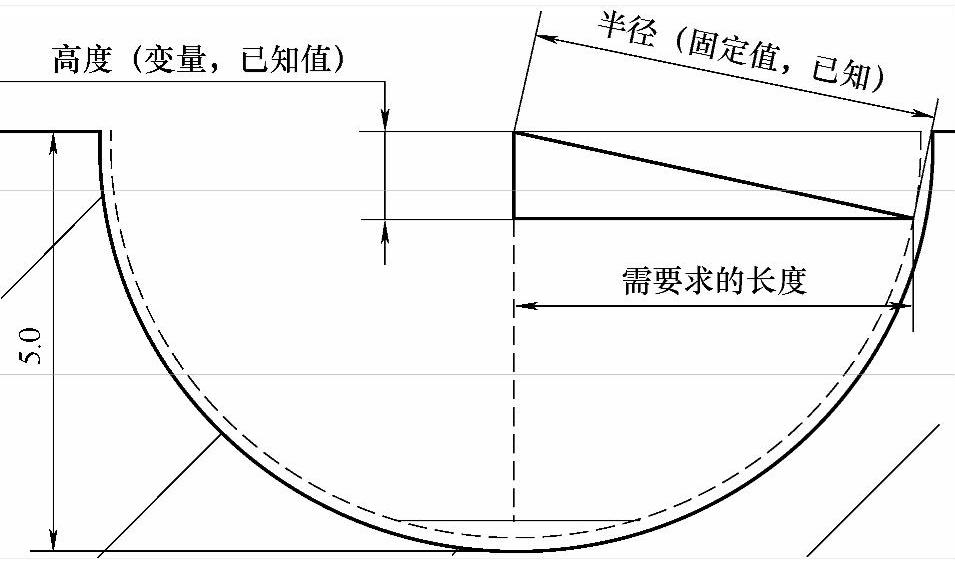
图 5-28
由图5-28就不难看出,需要的总长是多少,并且也知道该如何求。用公式表达就是:
当前借刀总长=[SQRT[半径∗半径高度∗高度]]∗23,式中之所以要乘以2,是因为左边还有一个同样长度(其中3是刀宽,别忘记减掉它!)。所以在车削的时候,只要把高度每次变化下,就能利用上述公式算出对应的长度,然后借刀即可。
万事俱备,现在开始编制加工程序了!
(在写宏程序的时候,是可以把中文注释信息写在小括号里的)
(螺距为13mm,刀具轨迹采用“先中间、后两边”。与梯形螺纹一样)
例5-16



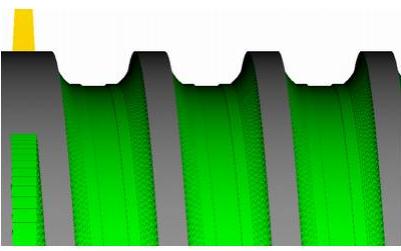
图 5-29

图 5-30
或许有读者纳闷,为什么总是使用“先中间、后两边”这个刀路?因为这最方便新手理解(还是那句话,你想让刀具怎么走,那就怎么编程)。
终于学习完加工程序了,等等,我们是不是忘了一件事?对,还没精车呢!没办法,只好继续了。
精车时,采用球刀,然后沿着R5mm圆弧的轮廓走一遍即可。但是球刀又有个问题:刀尖圆弧半径!
在华中数控或FANUC里,G32这一步是没法使用刀尖半径补偿的,系统总是报错。解决方案是通过系统变量得到半径补偿后的值,再放到普通变量里,再用G32车削。很明显,新手们看到这句话已经懵了!所以在此介绍另一种好用的方法——用圆弧车刀中心编程。(https://www.xing528.com)
用圆弧车刀中心编程,其实就是用车刀球心为对刀点,那么在加工时需要注意什么问题呢?还是通过示意图(见图5-31)来说明这个问题。
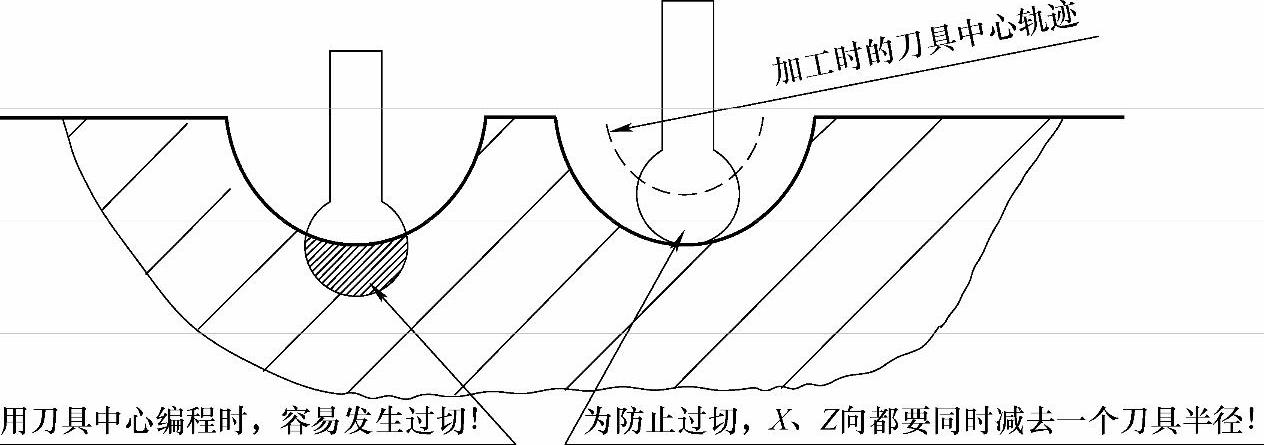
图 5-31
所以,在用圆弧车刀加工时,实际的圆弧车刀轨迹=圆弧牙型半径–刀具半径!解决了这个问题,就可以用球刀精加工了!另外,对弧面上的“点”如何求得,在本章开篇就讲到,别忘了哦。
例5-17


上述程序中最为关键的还是球刀定位点的问题。为何是16.5,而不是15请读者一定要弄明白。实在不行画画CAD图就一目了然。图5-32和图5-33 是加工效果图
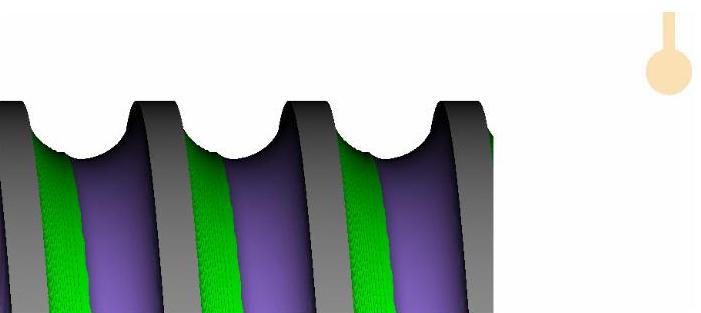
图 5-32

图 5-33
方法一主要介绍的是通过两把刀加工。接下来讲解如何用一把刀实现粗精一体加工。
要想一把刀实现粗、精加工,那么这把刀无疑是球刀了(圆弧车刀)。在加工时我们依然采用刀具中心编程。相关的注意点已经在方法一中讲解过,这里不再赘述。我们主要分析刀具轨迹以及效率问题。
方法二:球刀(圆弧车刀)实现粗、精加工(球刀半径R2mm)
在正式编程前要完成不少工作,首先就是刀具轨迹的分析!本例将采用X向偏移,把要切除的余量全部偏到零件外圆表面之上,然后再用递减的方法编制程序。刀具轨迹和G73类似,但又有区别。让我们看看图5-34所示的示意图。
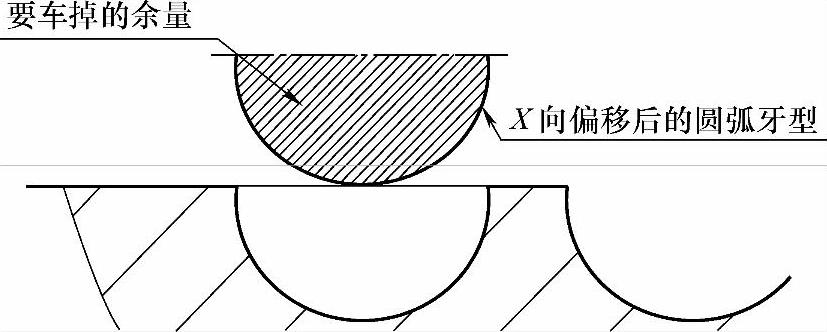
图 5-34
先把余量偏移出去,保证偏移后的圆弧最底部与外圆面相切。递减方法如图5-35所示。
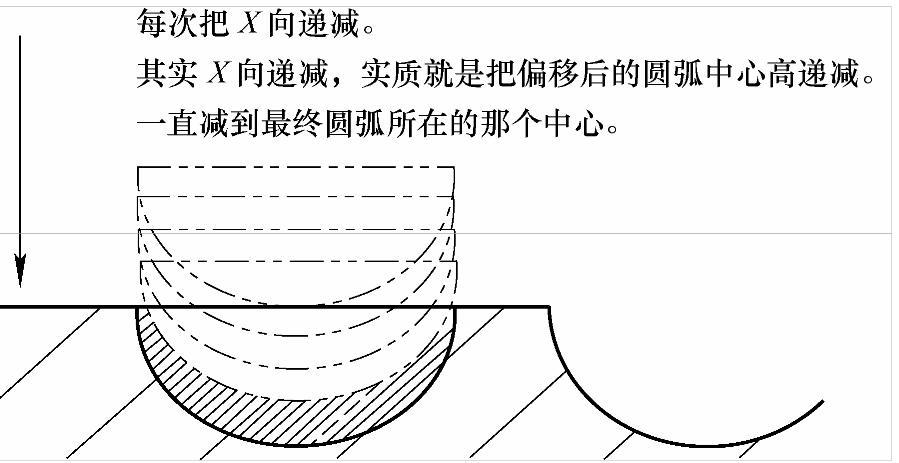
图 5-35
从上面两幅示意图可以看出,当把圆弧偏移之后,每一个圆弧都是精加工轨迹,只不过圆弧的中心距在慢慢降低,从而实现粗加工。但是此刀具轨迹有个非常严重的问题:空刀太多!
那么该如何处理空刀呢?在程序中揭晓!同时根据方法一的思路分析,已知实际加工时的圆弧半径,需要减去一个刀具半径,而且要用圆弧中心编程。这里不再赘述。
最后一个问题:要偏移多少呢?
前面说过,“偏移后的圆弧最底部与外圆面相切”。也就是说在外圆60mm的基础上加上圆弧半径5mm,那么双边就是10mm。所以最终偏移后的圆弧中心距离零件中心是70mm,如图5-36所示。
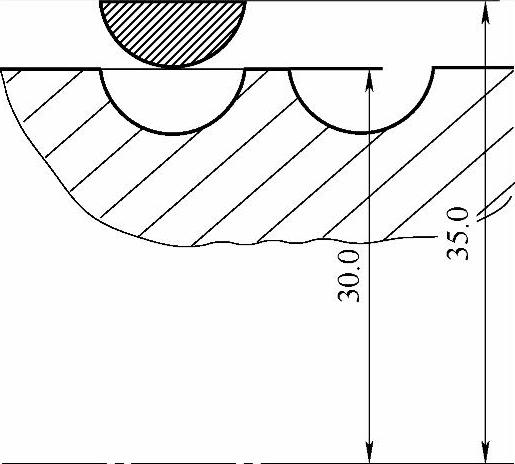
图 5-36
万事俱备,可以编制程序了!依然使用图5-26来编程
例5-18


上述程序诠释了“算法”两个字。实现了在一个程序里同时粗、精加工让我们看一下加工的效果图。
图5-37是粗车效果图。可以看出X向分层且每一刀的台阶比较明显。

图 5-37
图5-38是精车成品效果图。表面纹理与粗加工时截然不同

图 5-38
本节写到这其实已经结束了。但突然想起还有种刀具轨迹,所以一道讲完吧。
另一种刀具轨迹是“同心不等半径”。
顾名思义,就是有N个圆在同一个圆心,但半径会不断变大,如图5-39所示。
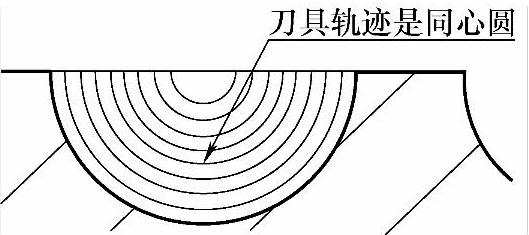
图 5-39
下面就来分析这个刀具轨迹。
由于这么多加工轨迹(圆)是同心的,且半径每次都在变化。一说到变化,让我们想想它能否是个变量呢?当加工好当前这个半径所对应的圆弧后,把半径变大,然后继续加工新半径所对应的圆弧。然后再增大一次,以此类推。一直增加到合格的牙型半径为止不就行了?所以可以肯定的是半径是变量!
半径每变化一次,都需要在0°开始重新加工。这说明什么问题?说明角度这个变量每次都需要重新赋值为0!这么一说,那就需要两层嵌套来完成这个动作了。而且角度变量是在里面一层的,这样才能每次被初始化为0。
分析完毕!可以开始编程了,依然使用例5-15的图样。
(由于该方法效率不高,所以不推荐用于加工。本程序旨在提高读者的程序算法能力)
例5-19


本节内容较多,请读者朋友不要心急,慢慢消化。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




