矩形螺纹参数计算、思路解析与宏程序编制

本节学习要点

1．牢记矩形螺纹的参数计算公式

2．完全吸收矩形螺纹的加工思路

3．掌握例题程序的编程方法

如果说宏程序在数车加工中，哪一块具有很高的价值，那么无疑是大螺距螺杆的应用了。第4章讲解的非圆曲线，其实也是为大螺距螺杆做铺垫。因为有些螺杆的牙型是非圆曲线形。

本节讲解的是矩形螺纹。

说到矩形螺纹，它主要用于传动机构，特点是传动效率较其他螺纹高。但对中精度低，牙根强度弱，同时其精确制造比较困难。此外计算还是比较容易的。

理论上讲，矩形螺纹的牙型为正方形。但由于内外螺纹配合时必须有间隙，所以实际牙型并不是正方形。它的基本尺寸计算公式如下：例5-1图5-1 l

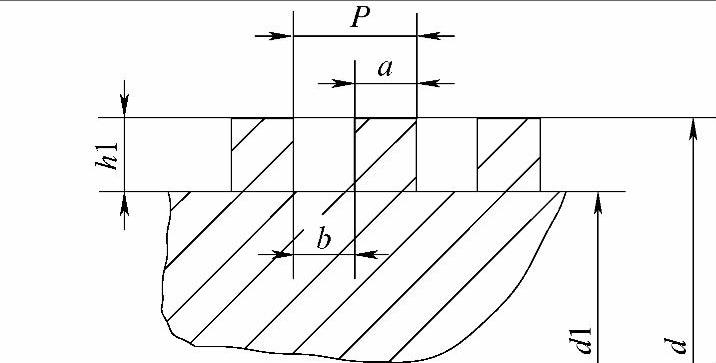
图 5-1

牙槽宽度(b)=0.5螺距(P)+（0.02一0.04）mm齿宽（a）=螺距（P）—牙槽宽度(b)

牙高（h1）=0.5螺距（P）+（0.1～0.2）mm

螺纹小径（d1）=螺纹大径（d）−2牙高（h1）

所以车削矩形50mm×8mm螺纹时，它的各个部分的计算如下

牙槽宽度=0.5×8+0.02=4.02

齿宽=8−4.02=3.98

牙高=0.5×8+0.1=4.1

螺纹小径=50−2×4.1=41.8

基本理论学习完毕，可以看看具体的零件图样了。

例5-2

图5-2是要加工矩形60mm×10mm螺纹。可以根据公式算出所需参数。但重点并不是计算，而是刀具轨迹。

在加工矩形螺纹的时候，由于刀具也是方头的（类似于切槽刀）。所以一般采用直进法加工。但当螺距较大、牙槽宽度比刀具宽度大的多时，需要借刀借刀的方式也有很多种，总的来说，你想怎么借刀，那就怎么编程。本例将采用两种借刀方法供读者参考。

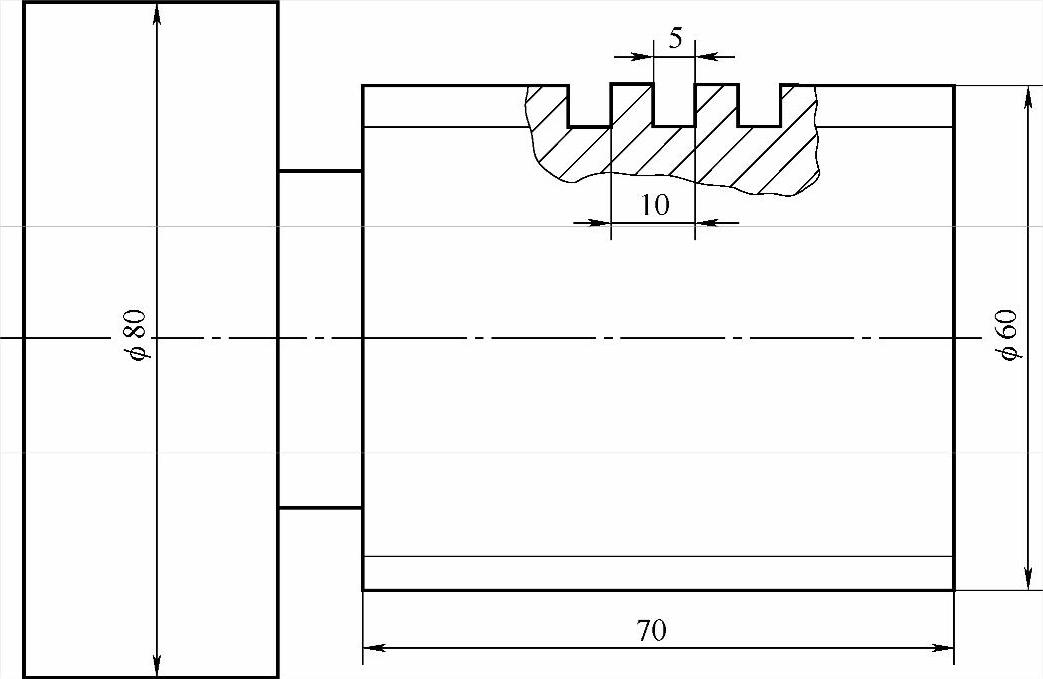
图 5-2

方法一：X向分层，Z向借刀

加工思路分析：

当采用方法一加工时，我们至少需要做两次判断。第一次是判断有没有车到某个深度。第二次是，在对应的深度上进行Z向借刀时，牙槽宽度有没有借到位。

对X向切削深度分层，其实就是每一刀的背吃刀量。在这里取每刀0.1mm（背吃刀量在实际加工时，可根据零件材料与刀具材料自行取值）。

在Z向借刀的时候，由于刀具自身有宽度，所以实际要借的长度是：牙槽宽度−刀具宽度。上面这两点弄清楚后，让我们再想一想程序的结构。

如果要在当前某个深度上进行Z向借刀，说明借刀这一步一定在X切削深度循环之内，并且X切削深度在Z借刀完毕之前不能改变（见图5-3）。也就是说程序的结构是两层嵌套。弄清这一点，可以试着编写方法一的程序了。首先根据图样可以计算出需要的参数。

图 5-3

例5-3

牙高=0.5×10+0.1=5.1

在上述程序中，如果Z向借刀的长度比刀宽大，那么就只能借刀具宽度的90%最佳。并且在判断的时候，需要考虑能否整除的问题。背吃刀量也是一样。这一点在前面已经讲解过，这里不再赘述。(www.xing528.com)

另外，程序可以简化，不需要这么“清晰”。当然，这里作为讲解，同时也考虑到很多朋友是初次接触，所以不得不这么写。如果读者有一定的宏程序基础，可以试着把程序简化。

让我们看看程序仿真、借刀效果图：

图5-4就是在车削好每一层X向深度后，会同时Z向借刀。再看一下成品效果图，如图5-5所示。

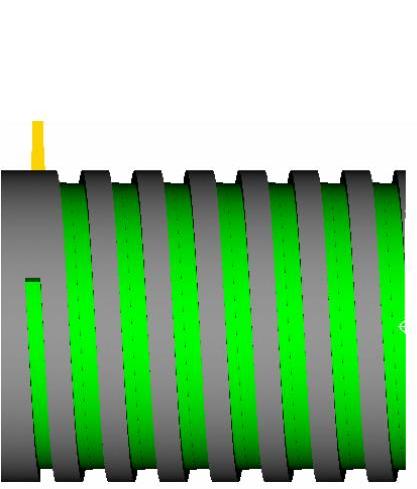
图 5-4

图 5-5

现在让我们再看看其他方法方法二：中途不需要Z向借刀（见图5-6）

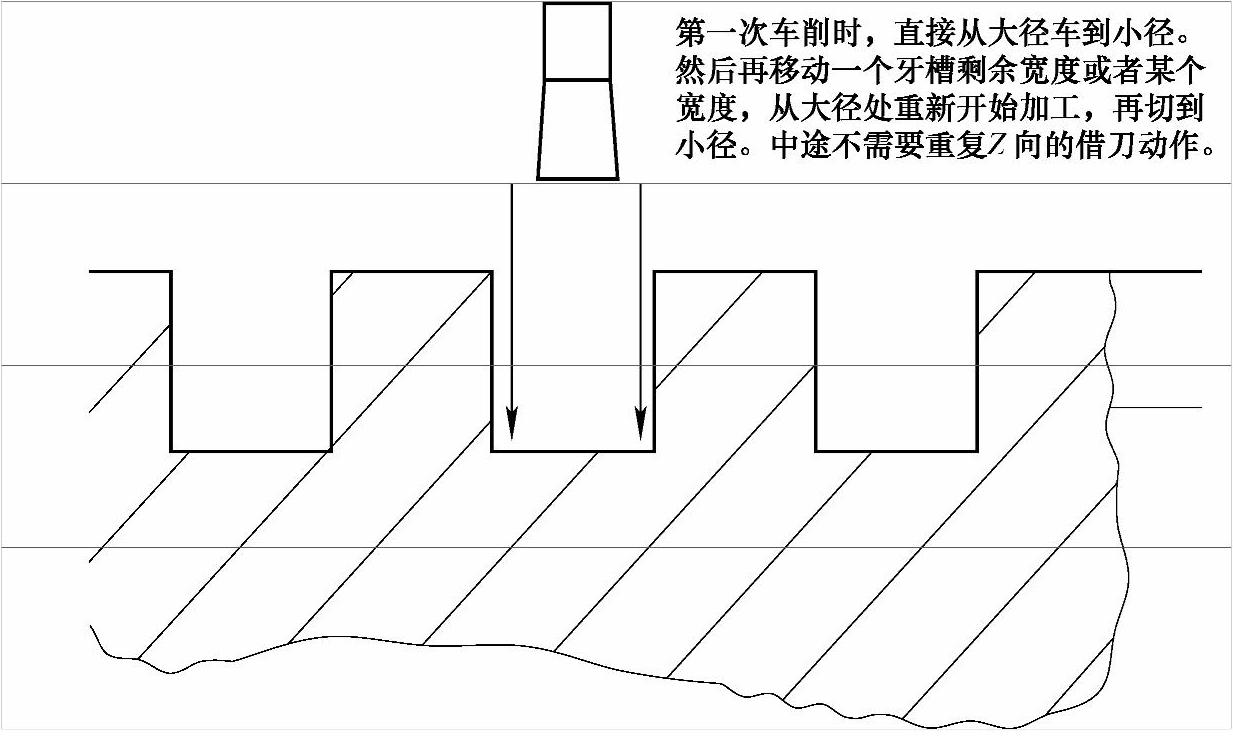
图 5-6

分析一下方法二的加工思路：

如果用该方法车削矩形螺纹，程序结构就更清晰了。只需要在X向单独操作就行。一直车到牙底为止。从这一点看，完全可以写两个单独的循环程序，只不过这两个程序之间，错开一个剩余的牙槽宽度而已。直接上程序。

例5-4

让我们看下加工效果图：

很明显，方法二是先切好第一层总深，然后再移动一个距离，进行第二次深度加工（见图5-7）。与方法一的最大不同在于：车削过程中，Z向没有借刀动作！图5-8是加工完毕效果。

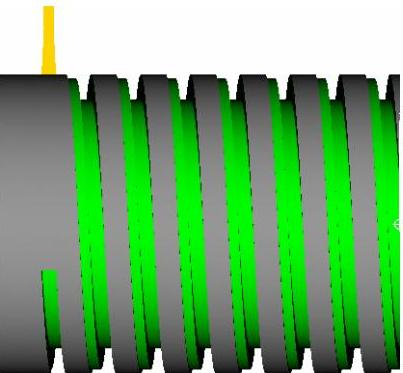
图 5-7

图 5-8

上述程序虽然可以加工出零件，但程序显的不够紧凑。那有没有逻辑紧密且在一个程序内完成该动作的方法呢？

方法还是有的。该方法两大层车削的不同之处在于：第一大层X车完后需要在Z向移动一个距离，然后继续直进车削第二大层的X向余量。此时第一层和第二层的X向切削深度动作是完全一致的！如果能够在程序中做到“改变Z起点”的话，然后X向切削深度用同一个循环程序，就可以在一个程序内加工该螺纹了。让我们试试看！

例 5-5

大致看下程序，会发现循环语句内用了四条“IF”语句，正是这四条“IF”语句才得以让程序“合二为一”。

乍看之下有点懵，一步步分析后就没那么懵了。

1）如果要在一个循环程序内完成两个动作，那么当#1从0加到5.1，Z向开始错开一个距离时，X向应该是从60mm处重新加工。而#1已经是5.1了，该如何把#1的值改为0呢？很简单，对#1重新赋值即可。因此程序中使用了“IF[#1 EQ5.1]THEN#1=0”语句。它的意思是，如果#1的值变为5.1的时候，说明第一大层X向已经车完，需要车第二大层了。所以就把#1的值重新赋值为0。

2）对#1的重新赋值，解决了X向重新车削的问题。那么在第二次切削时，Z向需要偏移一个距离（即剩余的槽宽），所以程序中对#2做了个“手脚”。

在第一大层全部车完后需对#1重新赋值为0，那么在程序中我只要判断#1的结果是不是又为0了，就能知道是否需要对#2进行处理。因此程序中“IF[#1 EQ 0]THEN#2=2.02”这一步就是当#1重新被赋值为0的时候，对#2也开始重新赋值。一旦#2有了新的结果，那么语句“Z[15−#2]”开始产生效果，实现Z向位移。

所以不难发现，分析中的第一和第二步是同时被执行的！

上述两个问题解决了，是不是程序就对了呢？其实不然。对#1、#2的处理并不是该程序的核心，而是如何跳出死循环。初学的朋友或许会问，怎么会有死循环了呢？分析如下。

当#1被重新赋值为0，且#2也同时被赋值为2.02的时候，程序开始执行第二大层的加工。但是当#1的结果又变为5.1时，#1紧接着被立刻赋值为0，同时#2也被赋值了。我们会发现此程序不论怎么车，就是出不来。因为#1的值满足条件就会被重新赋值，一旦#1为0，是满足循环条件的！所以程序中的#3F所在！该变量一开始被初始化为0，在程序刚执行的时候，由于#1初始值是0，所以语句“IF [#1 EQ o]THEN #3=#3+1”执行后，#3的结果是1。这是第一次被执行。第二次是在准备车削第二大层的时候，#1被语句“IF [#1 EQ 5.1] THEN#1=0”重新赋值为0。一旦#1为0，那么“IF [#1 EQ0]THEN #3=#3+1”就会执行，这时候#3的结果是2。当#1第二次执行完毕，它的值是5.1。在遇到“IF [#1 EQ 5.1] THEN #1=0”又被重新赋值为o。

这时候程序开始返回到循环开头处执行，此时“IF [#1 EQ o]THEN#3=#3+1”语句又执行了，#3的值就是3。而下一行便是判断语句了“IF [#3 EQ 3] GOT02”。如果#3的结果等于3，就跳转到N2段。而程序中N2段位于“GO Xl00”处，于是就开始退刀，程序结束！

最后一个程序，它的逻辑性比前面两个要强，如果你是初学者可以暂时不深究第三个程序。把前两个完全掌握即可。事后要找图样练习！