本节学习要点
1.掌握抛物线的方程化简、转换方法
2.掌握例题中的程序
上一节中讲到了椭圆曲线的宏程序编制,还补充了其他形态。本节开始讲解抛物线的宏程序编制。
其实不管什么类型的二次曲线,思路和方法都是一样的。唯一不同的是它们的方程。我们直接看图!
例4-15(图4-11)
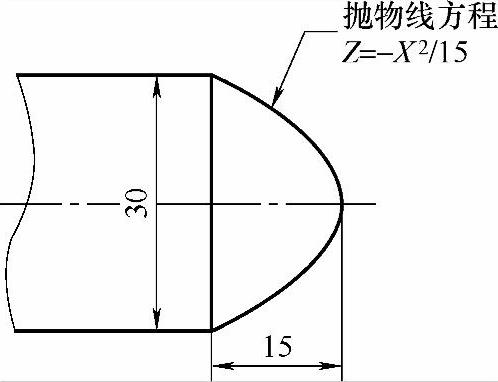
图 4-11
上面这个抛物线的方程,是用X作为自变量的。而前面讲过一般用Z作为自变量比较好。这里就用这个方程,把X作为自变量试试,看如何编程。
首先看到图样,要能想到一个关系:当X为0的时候,Z也为0;X为15的时候(单边),Z就是15,当然还有个负号。另外,图4-11中X的变化范围应该是0~15。因为零件最终最大外圆就是30mm。想到了这些,就可以编程了!
例4-16


上例就是用X作为自变量的程序,如果用Z作为自变量,需要把方程做一个转换,即 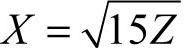
或许读者会问为什么负号不见了?其实方程里的负号只是决定Z走向的可以暂时把它去掉,然后在程序里加上就行,不然带着负号一起转化方程,说不定会把你弄糊涂。下面看看程序吧!
例4-17


由此可见,宏程序非常灵活。当你慢慢体会到这一点的时候,可以做到“随便整”。切记思路第一,程序只是表达思路的手段。
正如前面的椭圆一样,抛物线在零件中也有很多形态,下面让我们一起看看吧。
例4-18(图4-12)
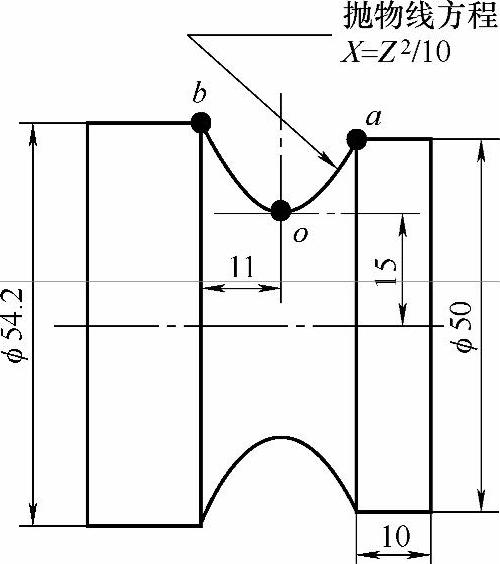
图 4-12
图4-12的抛物线开口向上。与第一个例题有所区别。(https://www.xing528.com)
不用管它上面开口朝哪,只要知道方程在哪,然后找出数据关系,其他的数学问题统统不用管。
分析图样可以得知,这个抛物线是位于外圆之上的。但这里有个问题,抛物线在图样中貌似是“凹”下去的,那是不是和椭圆一样,用中心高减去双边X值呢?这个结论我觉得下得有点早,最简单的方法就是把数据带进去算,我们试试看!
首先点a的Z向位于抛物线自身坐标原点的位置是10(从方程处得知)。如果把10带到方程里面算算X点的位置,就会发现也是10(直径值20)。但图样中该点的X向应该是50。貌似还差个30,但是别忘记还有个中心高度呢!
从图4-12中可以看到,中心高是15,直径值不就是30吗?那么30加上20不就是50了?所以,这里的抛物线看起来是凹的,但不代表肯定是减!
因此,读者一定要学会分析问题,看本书的真正目的,我觉得是学解决问题的思路,且不拘一格!
现在可以编写程序了。
例4-19

例4-20(图4-13)
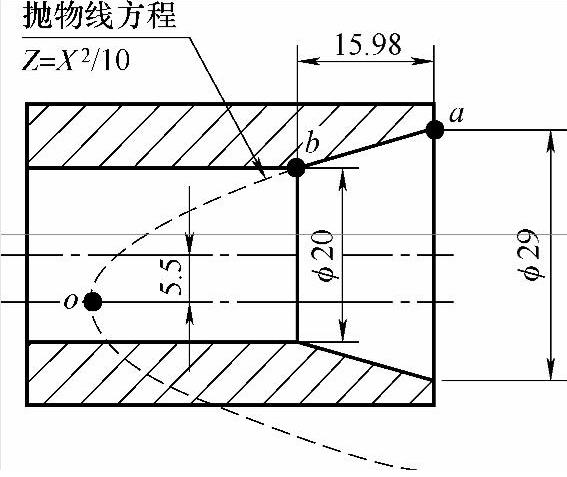
图 4-13
这幅图样乍一看比较复杂,尺寸也比较多,首先我个人习惯是把方程转
换一下 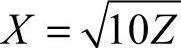
然后分析#1的初始值(即抛物线第一个点的Z坐标)。
在实际加工时,起点a的X坐标是29,但要找#1的初始值,就得考虑抛物线自身坐标系。所以起点a的坐标不是29,而是29/2+5.5=20。那把20带到方程算算,看#1(即Z起点)的初始值是多少。经过计算,初始值应该是40所以#1的初始值就是40。
其次再看看该抛物线的判断终点是多少。
由于图样中,实际抛物线轮廓长度是15.98mm,而#1的起始值是40,那么终点是40−15.98=24.02。也就是说,当#1的值还大于等于24.02的时候,就还没加工完!
现在可以编制程序了!
例4-21


本节到这里就结束了。类似的零件并不多见,但为了后面的异型螺纹学习,务必完全掌握这些曲线的程序编制!
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




