本节学习要点
1.掌握坐标不共轴的程序编制思路
2.掌握竖椭圆的程序编制
3.掌握“过1/4”椭圆的程序编制
上一节中讲到了椭圆曲线的宏程序编制,但在实际加工的时候,椭圆形态可能没我们想象的那么“乖”。如图4-3一图4-6所示几幅图样。
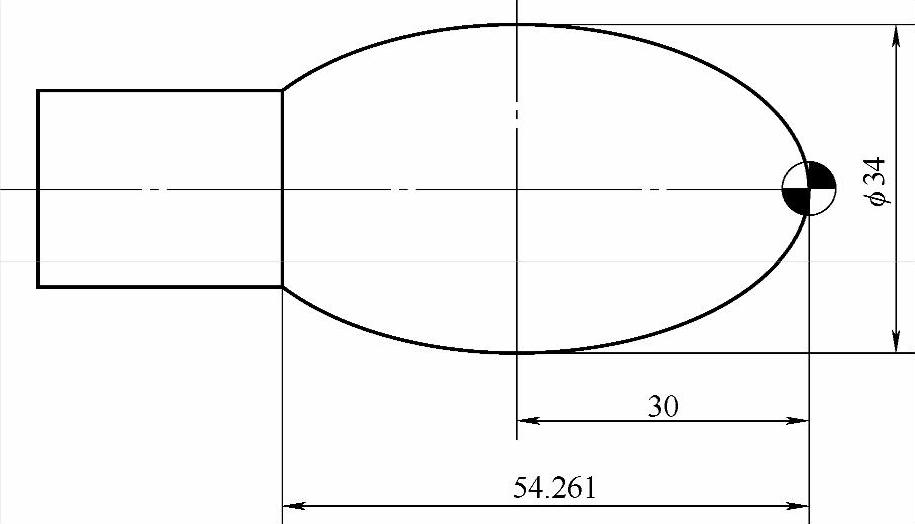
图 4-3
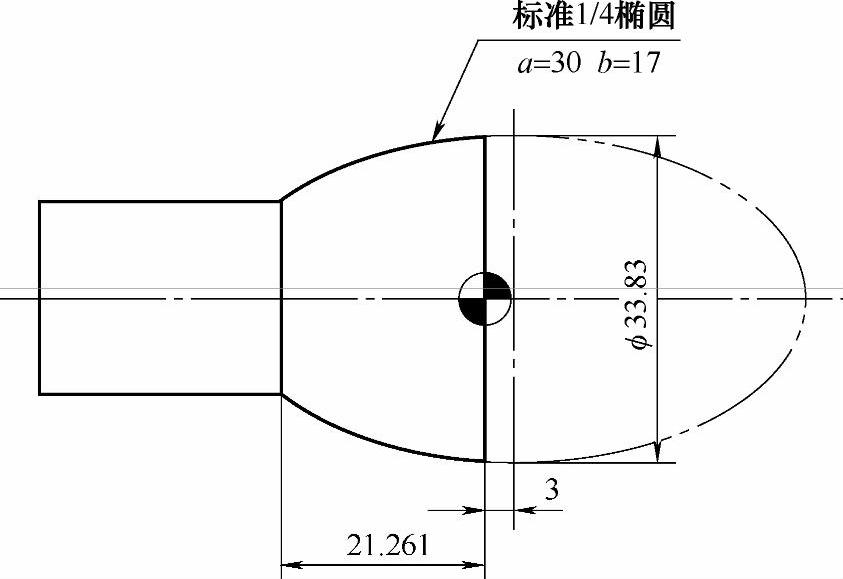
图 4-4
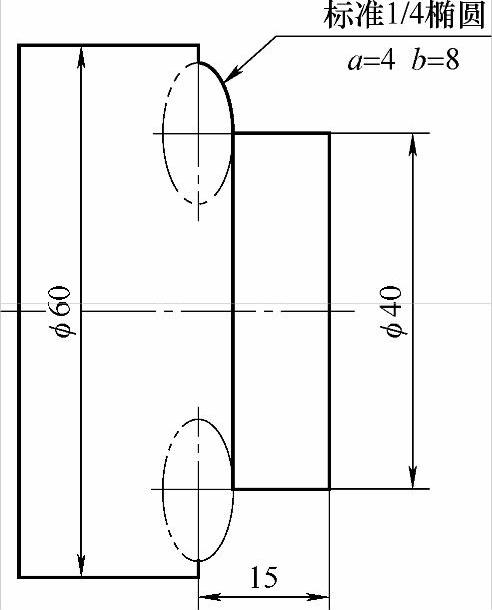
图 4-5
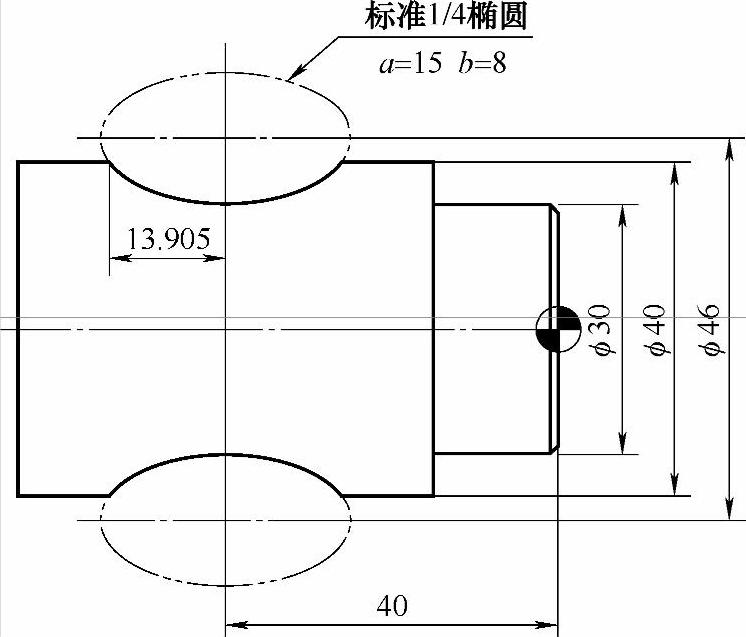
图 4-6
上面4幅图样椭圆形态各异。但它们的核心思路是一样的。下面我们来一一解答。
首先看第一份图样。
例4-7(图4-7)
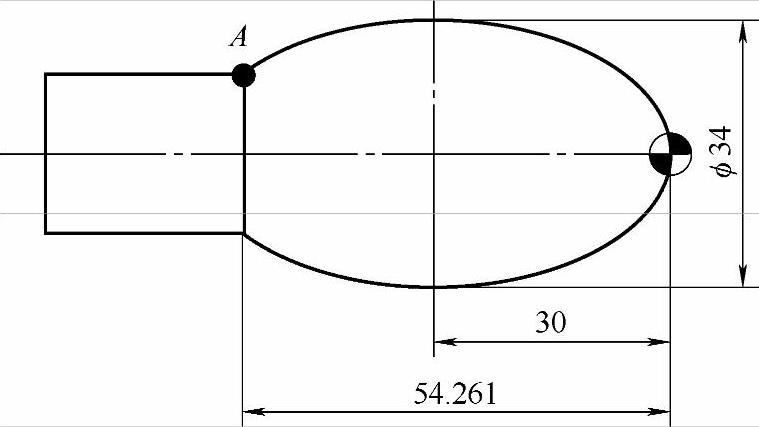
图 4-7
我对图4-7做了个标记,点A。这个椭圆与我们所见到的椭圆不同之处在于,它非1/4椭圆,而是超过了一半。所以我们的第一反应是该变量的终点不应该再是0,而是别的数。
仔细想想上一节做总结的时候,说过“在判断变量变化终点的时候,只要看曲线的最后一个点,相对于曲线坐标原点的位置就行。”所以,图4-7中曲线最后一个点是A,它相对于椭圆坐标中心的Z向距离是:54.261−30=24.261 切记,是相对于椭圆坐标中心,而不是零件坐标!
但是,点A是不是24.261呢?不是!正确的值是:−24.261。因为点A在椭圆坐标中心的左端,所以是负值。
经过以上分析,可以试着写写加工程序了(仅椭圆部分)。
例4-8

其实图4-3中的椭圆和之前遇到的是一样的,只不过#1的判断终点不是0,而是−24.261。但为什么是−24.261,这个一定要弄明白!
接下来看看第二份图样。
例4-9(https://www.xing528.com)
在图4-8中,我标记了两个点,分别是点A、点B。然后再结合图样发现A、B两点分别是零件中椭圆曲线的起点与终点。这两点相对于椭圆自身坐标系的位置分别是:−3、−24.261(注意不是−21.261)。所以我们自然而然地就想到#1的初始值是−3,终止值是−24.261。下面开始编制程序。
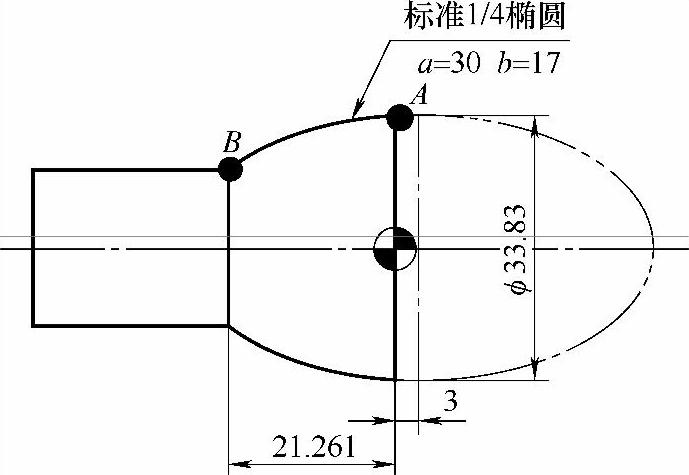
图 4-8
例 4-10

在图4-8中,特别要注意的是判断终点。如果被图样尺寸误导加工就会出问题。另外在Z[#1+3]这一步要明白为什么是加!
现在来看看第三份图样
例4-11(图4-9)
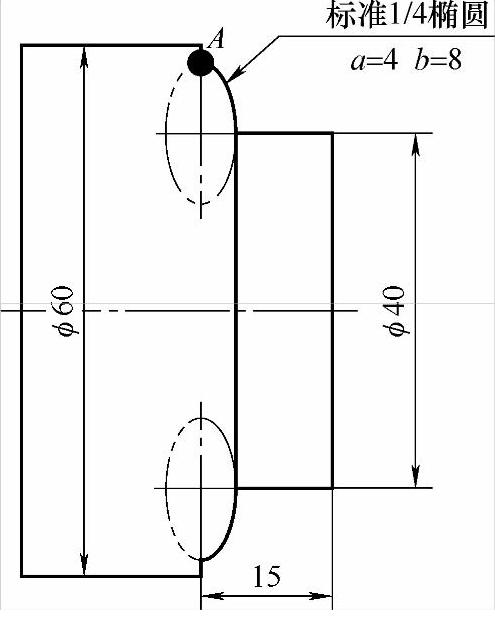
图 4-9
图4-9中的椭圆比较特殊,它是竖着的,另外在X向还发生了偏移。首先解决“竖”的问题(“竖椭圆”不是专业术语,但是本书重在让读者从形象的描述中学习到知识!弄一堆专业术语,不是作者的目的)。
椭圆之所以竖着,是因为长、短半轴对调了。所以在编程的时候,把长短半轴对调即可,没其他复杂的。
但是X向发生了偏移怎么弄呢?先看图中的点A,它是椭圆X向的最高点。如果没发生偏移,它的X坐标应该是16。但在图样中它却是56的位置。这是为什么?
因为椭圆的坐标基于φ40mm的外圆之上。也就是说实际加工的时候,在X向都要加上40,这样才能车出合格的零件。如果没加40那就等着撞刀了!
看看程序该如何编写。
例4-12
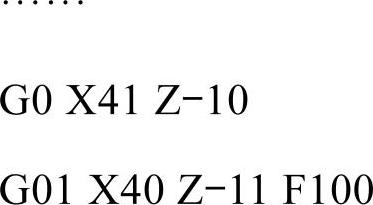

由程序可知,不管横、竖椭圆道理都是一样的
最后看看第四份图样吧!
例4-13(图4-10)
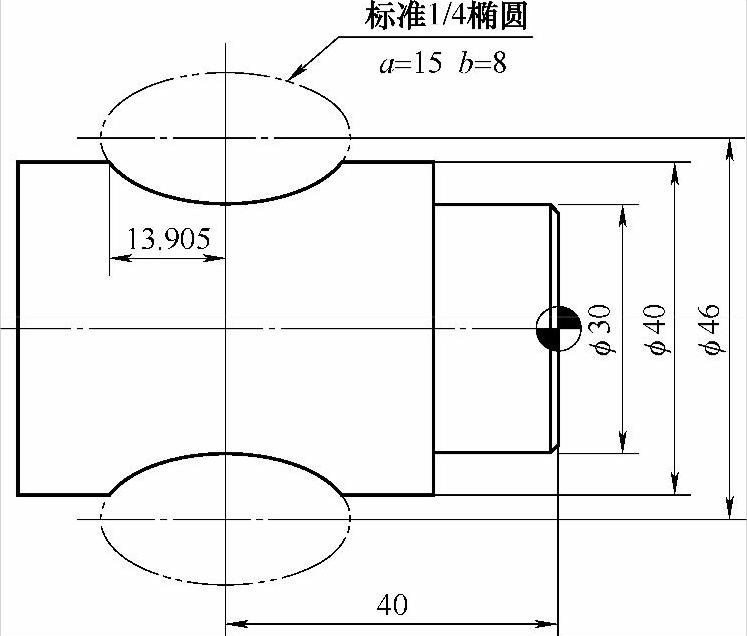
图 4-10
图4-10在形态上也是在X向发生了偏移,但是它的椭圆轮廓是凹下去的在潜意识里,如果凸椭圆是加,那么凹椭圆轮廓就是减了。没错,是这么回事!例4-14

上面的4份图样仅仅是典型,我们要学的是触类旁通。千万不能太死板!本节就到这里结束了,望读者朋友能够多找些其他例子练习。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




