椭圆曲线宏程序编制思路及实例程序

本节学习要点

1．完全掌握方程化简的方法，以及目的

2．了解自变量、因变量的选择前提

3．完全掌握非圆曲线的走刀轨迹

进入本节，也正式开启了宏程序编程之旅。

在宏程序的世界里可以做各种零件轮廓，特别是在数控车床技能大赛图样里，轮廓花样之多让人眼花缭乱。其中会经常看到一些曲线，它们无法直接通过G2/G3来加工，如椭圆、抛物线等。虽然现在的数控系统，有些G代码可以直接加工类似的曲线，但不全面。或许你也可以用CAM软件进行自动编程，但我认为，掌握曲线的宏程序编制是非常有必要的！很适合新手理解宏程序，并且慢慢体会到宏程序的精髓-；1具轨迹！所以从本节开始将逐一介绍数控车床加工范围内，可能会遇到的非圆曲线。

先看第一个最常见的曲线——椭圆。

与其他同类书籍不同，本书不会一开始就大谈程序，为时尚早！我觉得该先谈谈加工非圆曲线该分哪几步：

1．方程化简

化简方程的目的是更好理解等号两边的数值关系。

2．确定因变量、自变量

确定这两个量的目的，说白了就是让方程能够“动”起来。所谓自变量就是自身会主动发生变化。而因变量，它是因为其他变量变化而变化的量，属于被动变化。如例4-1所示。

例4-1

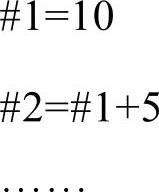
显而易见，这里#2的结果是15。

如果#1的值是12的话，那么#2的结果就是17了。#1是18，#2的结果是23。当#1的值发生变化了，#2随之也发生了变化。在上述例子中，#1就是自变量，#2就是因变量。因为#2总是因为#1的变化而变化。

3.编程时同时考虑曲线数学坐标与零件坐标

在编制曲线宏程序的时候，曲线自身是有坐标系的，而加工零件时也有坐标系。说通俗点，曲线自身坐标系的零点位置，不可能总是与零件坐标系零点重合。这两个坐标系之间需要“转化”。

上述三个问题都搞定了，就可以进行程序的编制。其中第三点会在程序里表述出来。首先解决第一个问题：方程化简。

首先看一幅图样。

例4-2（图4-1）

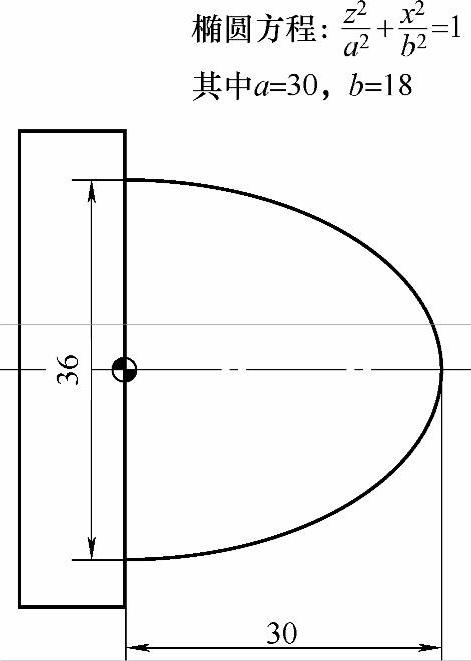
图 4-1

图4-1的图样告诉了我们椭圆标准方程，另外还知道该椭圆的长、短半轴各为30mm、18mm。或许有读者不知道什么是长、短半轴，但仔细看看图样应该不难猜出来吧！

图4-1中的方程，并不是加工时所需要的。我们希望得到的是X=...或者Z=...所以需要把方程化简。

化简步骤：

1.移项

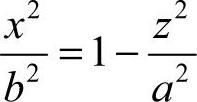
2.去分母

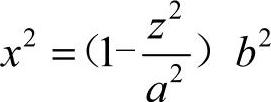
3.开方

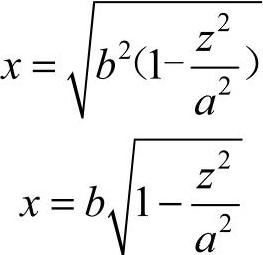
很显然，我们是把X向作为因变量，Z向作为自变量。在数控车床加工非圆曲线时，通常都这么做。当然也可以把X向作为自变量，Z向作为因变量。但在加工过象限的曲线时，会遇到问题。

化简解决以后，就可以进行下一步操作了。至于如何化简，可以多参考例子。

现在看第二个问题：确定因变量、自变量。

其实自变量或因变量，在化简方程的时候就已经确定了。比如本例以X向为因变量，什么意思呢？也就是说，当Z的值发生变化的时候，X的值也会跟着发生变化。它们俩有“因果”关系。在此真正要说明的是，方程中的X、Z表示椭圆曲面上某个点的坐标值。我们知道，不论是圆弧、直线或者曲线，它们都是由无数个小点组成的，然后点与点之间用小线段连接起来。只不过点与点之间的距离非常小，肉眼无法观察罢了。

取椭圆曲线上的几个点来看下。

例4-3（图4-2）

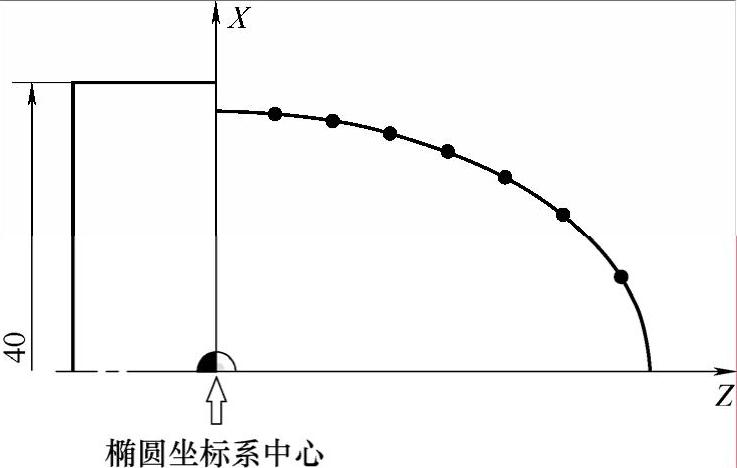
图 4-2

在例4-3中，在椭圆轮廓上随意取了几个点。正是这些点组成了椭圆曲线。方程中的X、Z就表示某一个点在椭圆曲线坐标系中的位置。如果让这个点的位置不断发生变化，并且用线段依次连接，这就成了椭圆！如果点的位置互相紧密，那么椭圆曲面就会光滑；反之“棱角”就会突出。(www.xing528.com)

关于第三点，会在程序中说明，这里就不介绍了。下面可以编制第一个曲线的宏程序了（注意，例4-4中的零件坐标系原点与椭圆坐标系原点重合，也就是在椭圆坐标系中心）。

例4-4

程序写完了，读者应该在大脑里“模拟”；刀具轨迹，看看对不对。

首先当#1=30的时候，开始执行WHILE语句，条件成立！于是进入循环部分。执行到了#2=...，由于#1的值是30，所以#2可以计算出来，等于0。计算好后，执行到下一行G01...。在这行，开始加工零件了。此时刀具在（X0 Z30）位置。然后开始执行#1=#1−0.1这行。这时候#1结果自减后，变成29.9。然后返回到WHILE语句开始判断，条件依然成立。于是继续执行循环体。这时候又来到了#2=...这行！由于#1的结果是29.9，所以#2的结果也变化了，不再是0。经过计算，#2此时的结果是2.94。之后执行下一行G01...，此时刀具在（X2.94 Z29.9）的位置，已经从第一个点走到了第二个点。最后#1再次递减，变成29.8。然后又回到了WHILE语句做判断，以此类推。一直到#1的结果不满足条件为止。

可以想象一下，当#1的结果是0的时候，X值就是36。意味着刀具位置在（X36 Z0）处。而到了这里，椭圆也车好了，再次判断时#1就不满足条件，于是退刀。

当然图4-1的图样也可以用IF...GOTO编程。程序如下：

例4-5

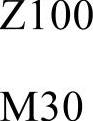
两种语句其实都一样，这里不用深入研究。

但是，在上面的程序中，使用的坐标系原点不在零件右端的旋转中心，而是和椭圆坐标系中心重合。实际加工中，零件坐标系原点一般都在右端旋转中心，如果这样的话，我们的程序该如何编写呢？或者说，这两者应该怎么转化呢？

其实我们思考下就会发现，如果把上述程序按照原点在右端来计算的话程序的X值是不存在问题的，但Z向就有问题了，第一刀就出了问题！

程序第一刀在（X0 Z30）处。但应该在Z0才对。然后Z值依次是−0.1、−0.2、−0.3等，一直到−30结束。如果按照上述程序加工的话，最后一刀Z值是0，相对于坐标原点在右端中心的零件而言，这才刚刚碰到端面呢！所以，程序中的Z向尺寸要做如下处理。

例4-6

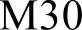
让我们把程序分析下就明白了。

当没处理Z向的时候，它的第一刀位于零件端面右边30mm处（因为#1=30），而我们需要的是0。那么如何把Z30变为Z0呢？方法有两个：

1.Z[30−#1]

2.Z[#1−30]

上面这两个第一刀都在Z0，但是第二刀对不对呢？按照程序的逻辑，第二次时#1的结果是29.9，这个值带进去计算就行。

1.Z[30−#1]<==>Z0.1

2.Z[#1−30]<==>Z−0.1

写到这，读者不难发现。第二个是正确的！因为刀具要向左边移动，那么Z肯定是负值。如果用第一种方法，那么Z向将越车越远。

所以可以在这里做个总结：

1）当#1的初始值不确定是多少的时候，那么就看图样中曲线第一个点

（Z向起点或者X向起点）距离椭圆中心的距离。这个距离就是#1

的初始值。

2）在判断变量变化终点的时候，只要看曲线的最后一个点相对于曲线坐

标原点的位置就行。比如本节例题，#1的终点是0。因为这是曲线Z

向上最后一个点，这个点相对于椭圆坐标而言它在0处，就这么简单。

3）当判断类似“Z[#1−30]”这一步的时候，如果读者发现第一刀起点并不

在加工需求起点时，可通过“手段”让它在需要的位置上！比如上例中

的#1−30。这么一来，Z起点就是0，符合图样的加工起点需求。

4）写程序的时候，一定要养成脑海中模拟刀具轨迹的习惯。这将对你以

后写宏程序有极大的帮助。可以做到手到擒来。

请读者一定要吃透本节的内容。非常关键！