掌握勾股定理的基本概念

本节学习要点

1．勾股定理的用法

2．完全掌握例题的内容

如果你是程序员，掌握一定的数学知识是很有必要的。不同领域的程序，对数学的要求也不一样。比如在数控加工领域，只需掌握基本的概念就好。

在加工的时候，遇到复杂的计算时一般采用CAD软件辅助“找点”了。但如果想学好宏程序，那么基本的数学知识还是要具备的！幸运的是，我们不需要掌握太多的数学知识，下面就介绍常用的一种——勾股定理。

可能很多朋友都学过，那是在初中的时候就讲到的概念。所以这里只是给读者做个简单的总结，如图1-1所示。

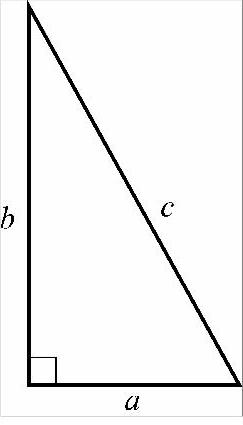
图 1-1

从图1-1可以看到，直角三角形中有a、b、c三条边，它们的关系是：两条直角边的平方和，等于斜边的平方，即：a²+b²=C²。根据这个等式，已知其中两条边便可算出第三条边的长度。比如要求出口边的长，那么表达式是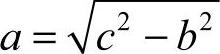： 。同理求c的边长就是 。但这里一定要注意，勾股定理只适用于直角三角形！

下面看一个数学上的例子，如图1-2所示

图 1-2(www.xing528.com)

图中标“?”的是要求得的尺寸，当然我已经通过软件得知这个尺寸。如果用勾股定理算该怎么求呢？其方法如下：

根据勾股定理可知：45²+20²=?²

结果是：49.244。

最后让我们看一份数控车床零件图样。在这份图样中我们要车削内孔轮廓，但孔的有效长度却不知道，这时候就可以用勾股定理算出，如图1-3所示。

图 1-3

首先我们该学会分析图样。如果想用勾股定理，那么必须“构建”一个直角三角形。既然求长度c，那构建的三角形一定要和c边有关。不难发现，图1-1中的三角形abc正好符合要求。那再看看o、6的长度是否已知。从图1-1中可以看出口的长度其实就是圆的半径15mm，而6边的长就是10mm。那就可以根据勾股定理公式算出c边的长了。

类似于上例的计算数不胜数，其核心就是构建一个直角三角形，并且这个三角形要和被求的那个边有联系，然后再找到其他两个边的长度，最后用公式套进去就行。

请读者一定要学会本节的内容。宏程序绝对离不开最基本的计算。