电气传动部分对位置误差的影响分析

暂且不考虑机械传递刚度等引起的误差，并假定驱动死区以及数字化死区很小，可以忽略不计，则整个系统可以简化为图3-109所示的数学模型。

1.对定位误差的影响

简化位置闭环控制系统的开环传递函数为

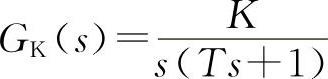
由此看出，该系统为典型的Ⅰ型系统，因此不存在位置定位稳态误差。其闭环传递函数为

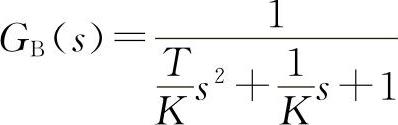
根据典型二阶振荡环节的特性，其阻尼比与振荡角频率为

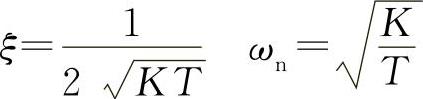
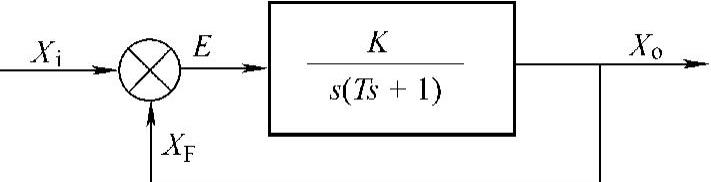
图3-109 电气传动部分数学模型

图3-110是当伺服系统的时间常数T一定，增加K值时位置响应曲线的变化情况。图3-111是当K一定，改变伺服系统的时间常数T值时位置响应曲线的变化情况。图中ω₀=1/T。

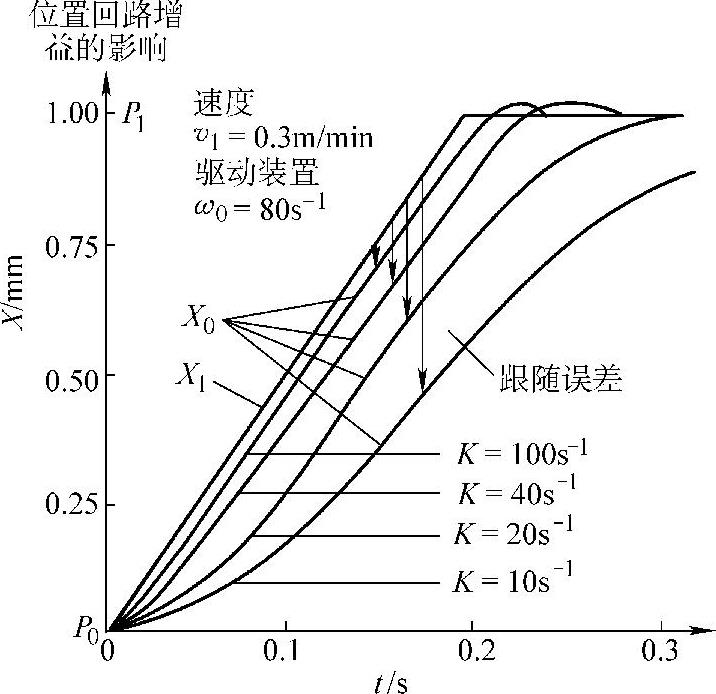
图3-110 定位过程位置响应曲线（T一定时）

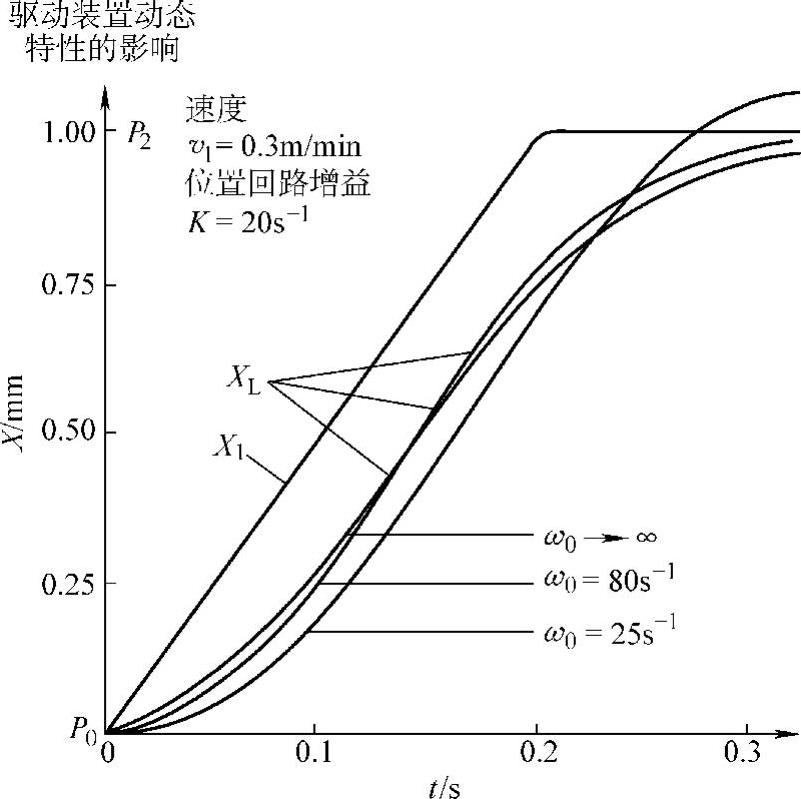
图3-111 定位过程位置响应曲线（K一定时）

由图可以看出，当T=0.0125s时，如果开环增益K超过20（1/s），则位置响应曲线就会产生超调。这与理论上二阶系统当ξ≥1时无超调是相符的。同理，当K=20（1/s）时，如果伺服驱动的时间常数过大，则位置响应曲线也会产生超调。由此可以得到以下结论：

①要想提高位置增益（较高的位置增益可减小跟随误差，缩短过渡过程时间，对减小轮廓误差也是重要的），必须有较小的伺服时间常数，也就是说伺服驱动装置的快速性要好。否则，提高位置增益会产生超调，而在数控机床上超调就意味着过切，这是不允许的。

②如果仅选择了快速性好的伺服驱动，而不提高位置增益，则整个系统的瞬态响应并不能得到明显改善，因此K与T的配合是很重要的。一般取K·T=（0.2～0.3）是比较合适的，这样既可以保证很小的超调，又可以保证良好的快速性。

③由于位置控制传递函数为Ⅰ型系统，因此在定位过程中（在恒速运动时）存在一个恒定的跟随误差。

E（s）=X_i（s）-X_o（s）

跟随误差对输入的传递函数（误差传递函数）

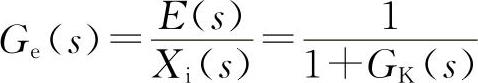
当以进给速度为V恒速运动时，其相当于斜坡输入X_i=V·t·1（t），则

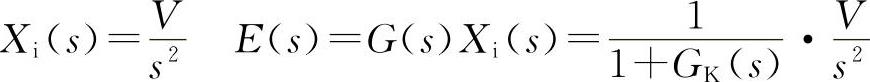
稳态跟随误差

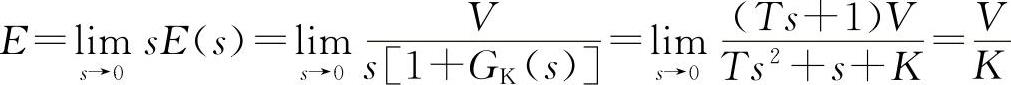
例如当某轴开环放大倍数为30（1/s），以其200mm/min的速度运动时，在任一时刻命令位置与实际位置的跟随误差。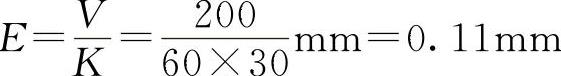

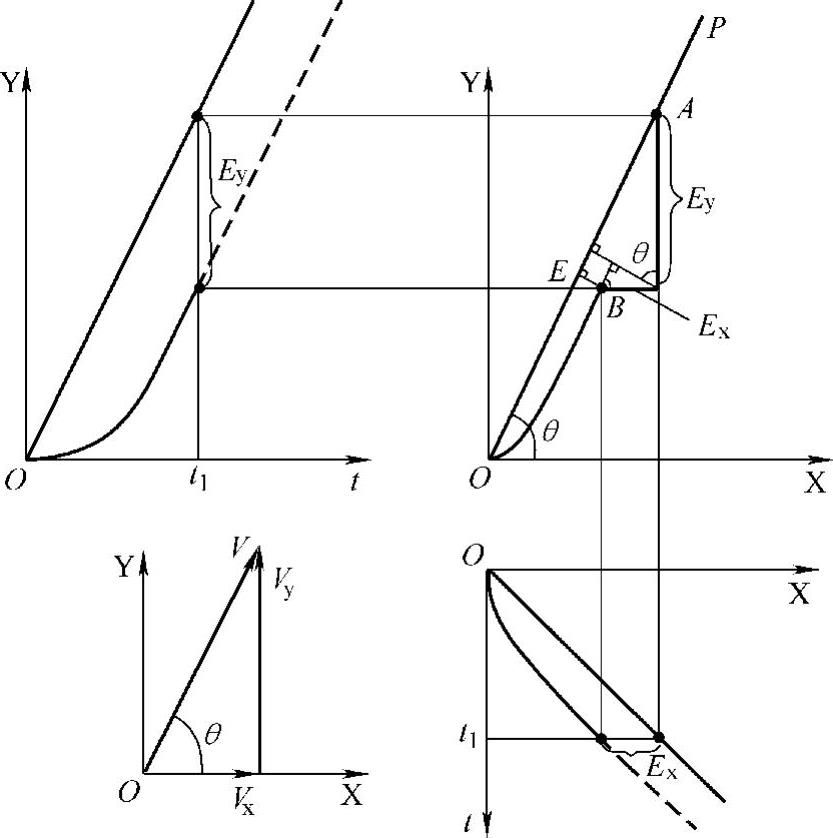
图3-112 直线插补轮廓误差与跟随误差的关系

2.对直线加工轮廓误差影响

由于不存在无限大功率的电动机，而且驱动对象总存在负载，因此跟随误差是客观存在的。如果使用或调整不当，则单个轴的跟随误差会造成轮廓运动的误差。

当数控机床进行XY轴直线联动插补时，其X、Y轴分别以恒速V运动，即x=V_xt、y=V_yt，此时各轴的跟随误差分别为E_x=V_x/K_x，E_y=V_y/K_y，如图3-112所示。

两坐标的合成运动构成实际加工轮廓轨迹，实际轮廓与编程轮廓之间的垂直偏离距离就是轮廓误差，记为E。E与E_x、E_y的关系如图3-112所示。图中，A为指令位置，B为实际位置。由几何关系可得

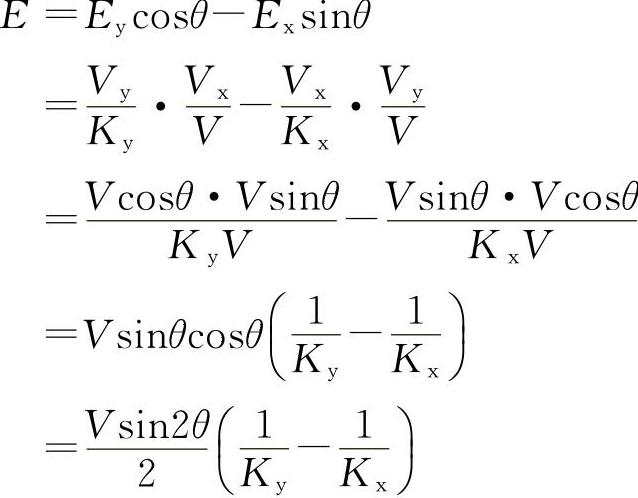
即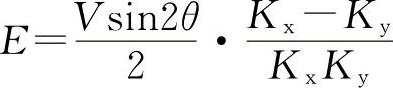由此可见：(www.xing528.com)

①当K_x=K_y，即两轴位置增益相同时，由于两轴跟随误差相抵消，轮廓误差E=0。

②当sin2θ=0，即θ=0°或90°时，轮廓误差E=0。即当沿着X或Y轴单轴运动时，不存在轮廓误差。

③实用中，很难保证K_x与K_y完全相等。由E的表达式可以看出，K_x和K_y越大、越接近，所产生的轮廓误差就越小。因此，使两轴位置增益匹配并尽可能提高是很有必要的。需注意的是，由于暂态过渡过程在数百毫秒内迅速完成，这里仅讨论的是稳态误差。与定位过程中分析道理相同，过高的位置增益会对暂态过程产生不利影响。

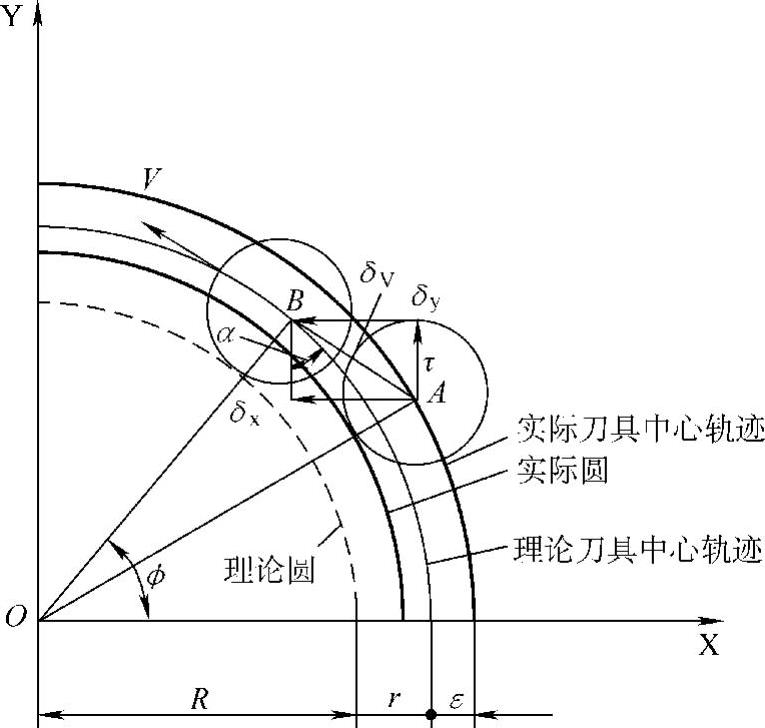
图3-113 圆弧插补轮廓误差示意图

④轮廓误差与编程进给速度成正比。

3.对圆弧插补轮廓误差的影响

圆弧插补轮廓误差分析如图3-113所示。图中，R为工件半径；τ为刀具半径；ε为圆弧加工误差；V为切削进给速度；K_x、K_y分别为X、Y轴位置增益；δ_x、δ_y分比为X、Y轴跟随误差；ϕ为OB与X轴的夹角。由图可知

V_y=Vcosϕ

V_x=Vsinϕ因此

在由三角形ΔAOB中，由余弦定理得

即

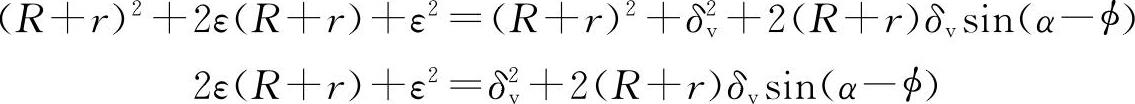
由于ε很小，ε²更小，可忽略不计，故

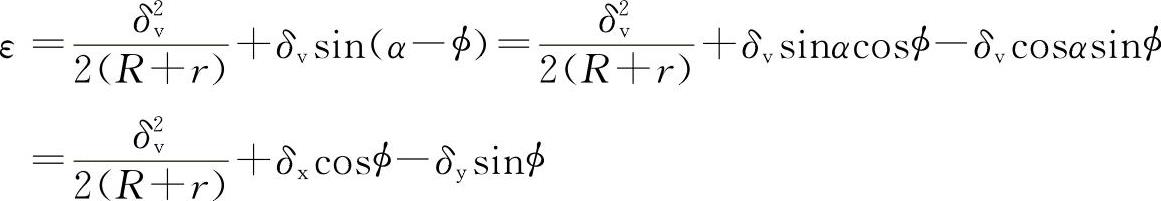
由于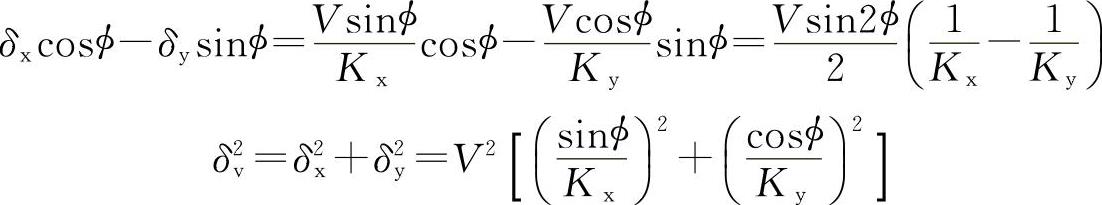所以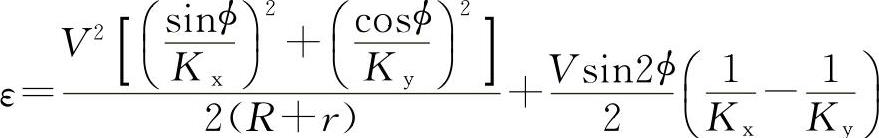

由此可得出以下结论：

①当K_x=K_y时，上式可简化为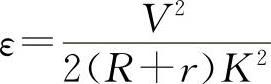，即当两轴增益匹配时，所加工出的实际轮廓仍为圆弧，ε为一恒定值，与ϕ无关，误差在于圆弧半径的大小不同。当要求加工精度高时，可通过编程时修正圆弧半径的方法来解决。同时可看出，ε与进给速度成正比，与位置增益成反比，因此提高位置增益对减小圆弧加工误差也是很重要的。

②当K_x≠K_y时，ε随着ϕ发生变化，所加工的圆弧将产生形状误差。当K_x与K_y差别不很大时，可忽略第一项中ϕ对ε的影响，而第二项的大小与sin2ϕ成正比。因此当K_x≠K_y时，所加工的圆弧将变成长轴位于45°或135°处的椭圆，如图3-114所示。同时可明显看出，当K_x=K_y时，提高K_x和K_y对减小误差ε有很大益处。

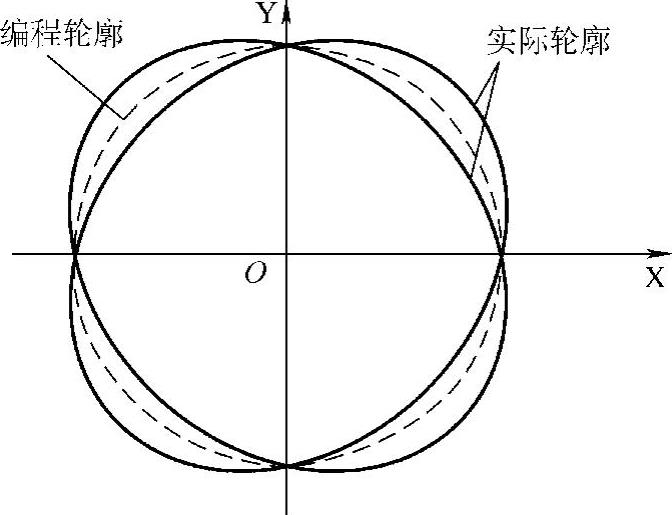
图3-114 增益不匹配时圆弧轮廓误差

4.对拐角轮廓误差的影响

数控机床在进行加工时，在两个轮廓（直线或圆弧）的交接处会产生误差，称为拐角轮廓误差。最简单和最容易理解的例子是沿着两个正交坐标轴加工拐角为直角的零件，如图3-115所示。当X轴的位置指令到达后，另一轴Y立即开始从零加速至指定速度运动。但是由于X轴指令位置与实际位置之间有V/K_x的滞后量，所以当Y轴开始运动时，X轴尚在B点，形成了图中所示的拐角误差。

当位置增益较低时，若为外拐角，则会切去一个小圆弧；若为内拐角，则会出现欠切削。当位置增益过高时，若为外拐角，则会在拐角处留下鼓包；若为内拐角，则会出现过切削。

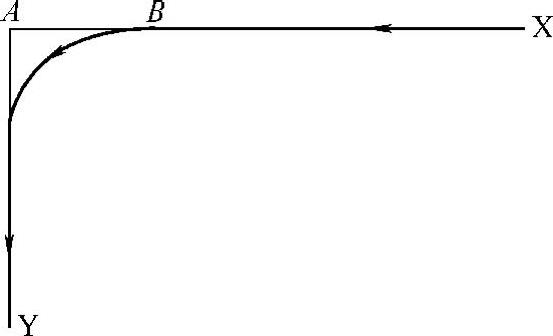
图3-115 直线加工拐角轮廓误差

拐角轮廓交接的情况是很复杂的，但只要注意以下几点，就可以有效地控制拐角误差的大小。

①选取动态性能尽可能好的伺服驱动装置，这样就可以选取较高的位置增益，而不会产生超调。

②如果对拐角误差要求较高，要尽可能降低切削速度，因为跟随误差与切削进给速度是成正比的。

③可在要求较高的轮廓交接处加入一条G04延时指令，延时数十至数百毫秒，在这段时间里前段轮廓加工时的跟随误差会迅速得以修正。

④采用尖角过渡指令（有些数控系统的指令为G07），此指令通常为一模态量。执行此指令后，数控系统在每一轮廓进给完成时，均要检查跟随误差是否小于一定的值（该值可由用户在参数区中设置）。只有当跟随误差足够小后，数控系统才会认为该段轮廓进给结束（即到位），下段轮廓的进给才能进行。

⑤使用数控系统的自动升降速功能，有利于在较小的增益时减小超调量，从而使用动态性能较差的驱动装置可达到使用动态性能较好的驱动装置的精度。除改善轮廓交接处的精度外，自动升降速还降低了加速度的值，从而减小了对精密机械传动部件的冲击，有利于机床精度的保持。