脉振高频电压注入法简介

脉振高频电压注入法只是在电机的同步旋转坐标系d、q轴中的d轴注入高频电压，这个高频电压在静止坐标系α、β轴中表现为一个脉振高频电压。

根据式（5-109）有

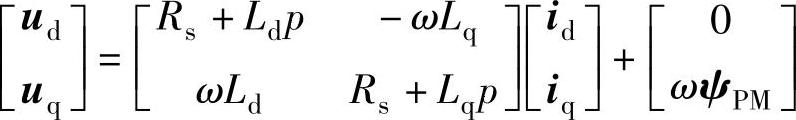
由于注入电压信号的频率要远高于电机转子频率，因此电机可以等效为R-L模型，根据dq坐标系下永磁辅助同步磁阻电机的电压数学模型，可以推出此时的高频电压方程为

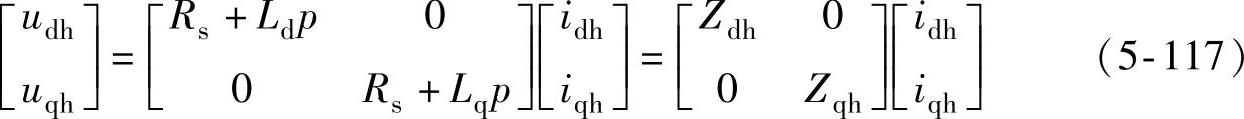
式中，Z_dh和Z_qh分别为d、q轴高频等效阻抗，定义转子位置信息估计误差Δθ为

式中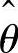，为估计值，θ为真实值，关系图如图5-30所示。

定义T（Δθ）为真实转子位置到估计转子位置的转换矩阵。

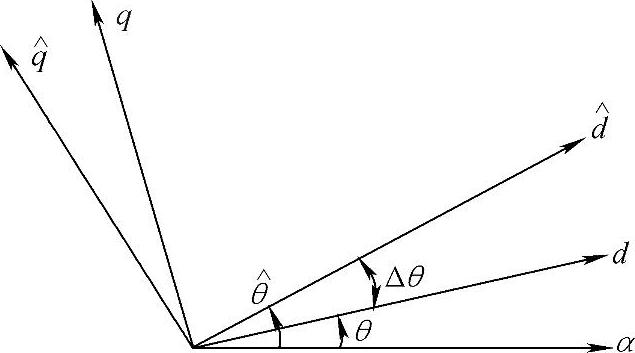
图5-30 估算转子位置和实际位置关系图

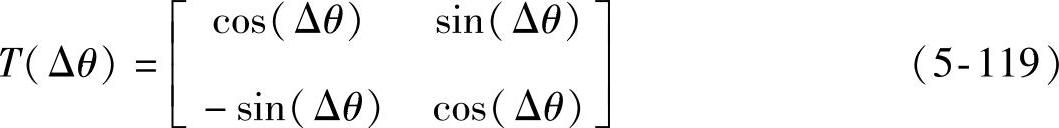
则在旋转坐标系d、q轴下，高频电压和电流关系可以写成

化简可以得到

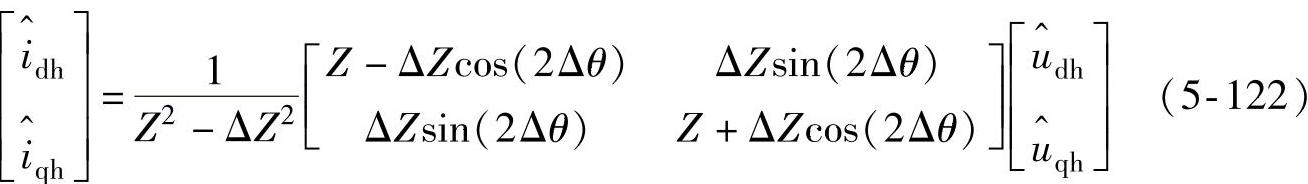(www.xing528.com)

式中 Z=（Z_d+Z_q）/2——d、q轴平均高频阻抗；

ΔZ=（Z_d-Z_q）/2——d、q轴半差高频阻抗。

假设在永磁辅助同步磁阻电机dq坐标系中，估计d轴注入高频正弦信号为

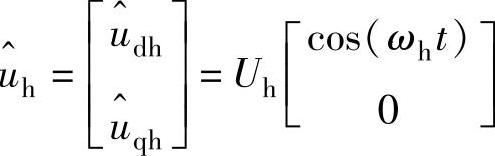
则式（5-122）可以表示为

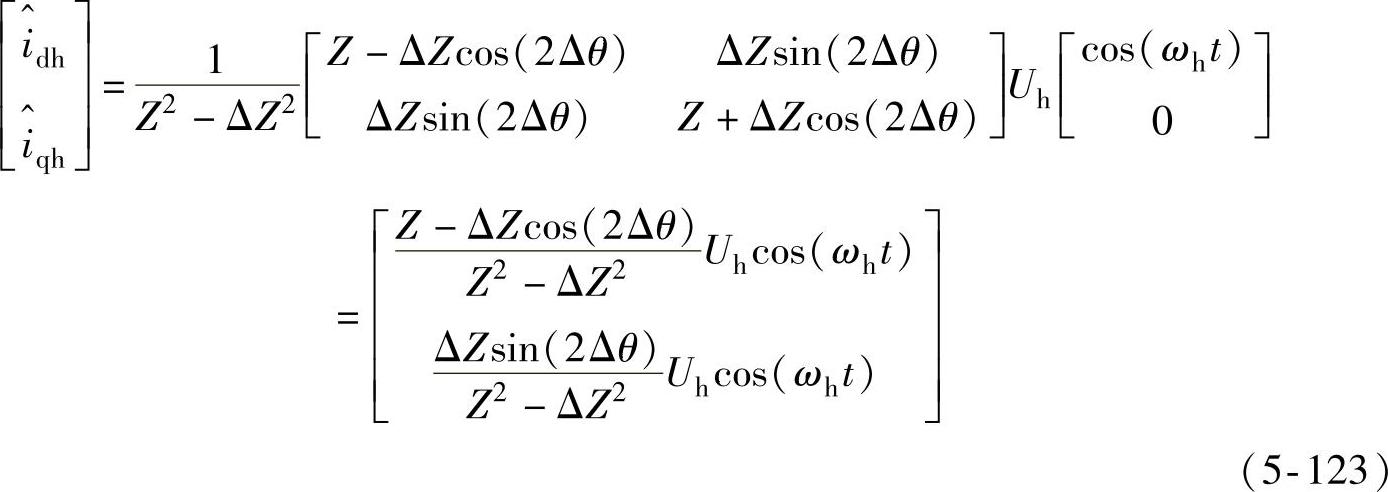
由式（5-123）可以看出，如果半差高频阻抗ΔZ不为0，则估计的旋转坐标系d、q轴中，d轴和q轴上的高频电流分量都与估计转子位置的误差Δθ有关。若Δθ为0，则d轴上的电流并不为0，而q轴上的电流为0，所以选择q轴上的高频电流分量进行相应的处理以得到转子位置信息，提取原理如图5-31所示，采集电机的三相电流经过坐标变换后得到估计的q轴电流，然后经过一个带通滤波器得到q轴的高频电流信息，再乘以调制信号sin（ω_ht）进行信号调幅，得到关于转子位置误差信息的函数。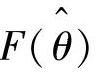

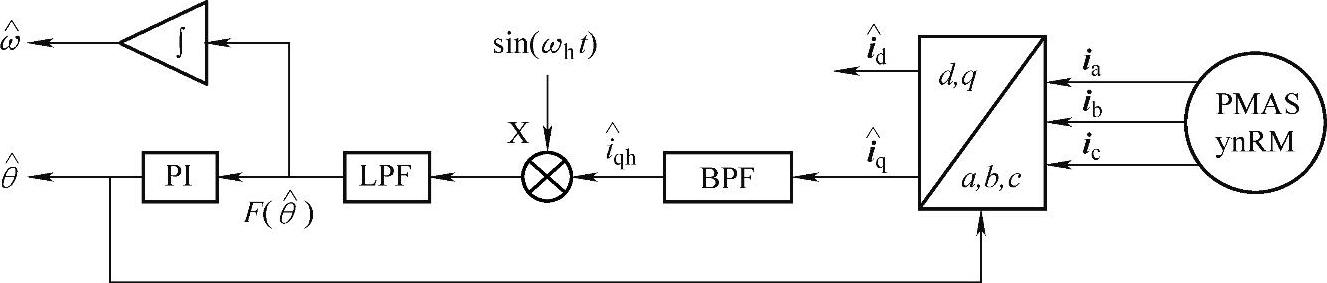
图5-31 转子位置信息提取原理图

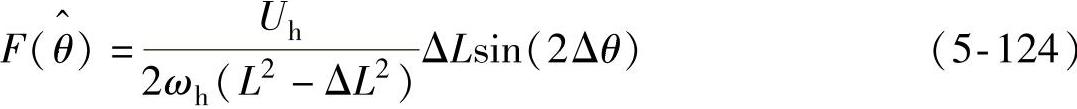
从式（5-124）可以看出，当Δθ接近0时，sin（2Δθ）≈2Δθ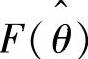，可以表示为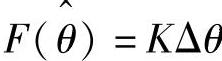，其中，K=（U_hΔZ/ω_h）/（Z²-ΔZ²）为误差增益。如果通过调节器把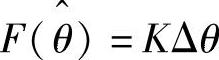调节为0，则估计转子位置信息误差为0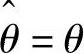，。在这里调节器采用PI调节器，如图5-31所示。

脉振高频电压注入法在误差函数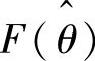趋近于0时存在两种情况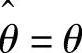，一种是，另一种是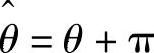。所以利用脉振高频电压注入法估算转子位置信息时，在起动时刻还需要进行极性判断，否则会存在起动失败的情况。

判断转子极性可以利用磁路饱和效应，脉振高频电压注入法可以通过直接观测d轴高频电流来判断磁极极性。当i_d>0时，定子电流与永磁体的磁链方向一致，d轴电感降低；当i_d<0时，定子电流与永磁体的磁链方向相反，d轴电感升高。利用这种特性可以辨别出电机磁极的极性。当Δθ接近0时，估算出的高频d轴电流可以表示为

根据以上分析，当估计转子位置信息与实际位置一致时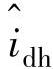，的正向幅值大于负向幅值；当估计转子位置信息与实际位置相反时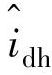，的正向幅值小于负向幅值。所以可以通过一个低通滤波器（LPF）来提取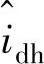的直流分量，直接通过判断直流分量来判断磁极极性。