滑模观测器在电机控制中的应用原理及设计

滑模观测器是滑模变结构控制的一种，其本质是一种特殊的非线性控制，滑模观测器系统结构是随着时间变化的。通过设计系统的滑动模态，强迫系统在一定条件下沿着固定的状态轨迹来回切换，即进入滑动模态。一旦进入滑动模态，控制对象的参数和外界的干扰就不起作用，因此滑模观测器具有对参数和外界的干扰不敏感、鲁棒性强和响应速度快等特点。

假设时变系统的状态方程为

F=f（x，u，t） （5-89）

式中，x为系统状态，u为控制函数，在S（x）=0发生切换，u可以表示为以下形式：

u+（x，t）、u-（x，t）和S（x）都是连续函数，而且u+（x，t）必须不等于u-（x，t）。

在两相静止坐标系α、β轴下，永磁辅助同步磁阻电机的数学模型可以表示为

从式（5-92）可以看出，电机的感应电动势里包含电机转子位置信息和速度信息，在中高速运行状态下，电机的感应电动势较容易观测出来，可以通过设计滑模观测器将电机电压和电流作为输入量，通过对感应电动势的观测将转子位置信息提取出来。

根据式（5-90）可以设计s=i′-i作为切换面S（x）。

由式（5-91）永磁辅助同步磁阻电机的数学模型构建基于滑模观测器的电机电流状态方程为

式（5-94）减去式（5-91）可以得到滑模观测器的电流状态误差方程

式中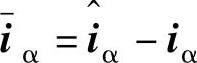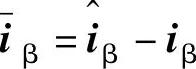，，，k为控制器增益。(www.xing528.com)

从式（5-95）可以看出滑模观测器的设计应当选取S（x）=-i作为切换面，选取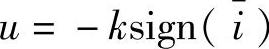作为控制函数。滑模观测器稳定的充分条件为。

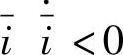同理

要满足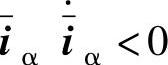和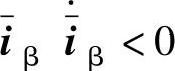，根据式（5-96）和式（5-97）可以求出当k>max（e_α，e_β）时，可以保证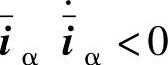和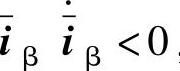，系统会进入滑模面并保持稳定。但实际应用中，k值不能过大，否则会引起估计电流的偏差和系统的抖振。

随着S（x）=0和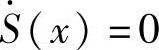，可得到

式（5-97）中右边的开关控制函数包含了感应电动势信息，但是开关控制函数还包含了高频开关信息，要经过低通滤波才能得到正确的感应电动势信息。

转子位置可以表示为

从式（5-99）可以看出感应电动势是经过低通滤波得到的，存在有相位延时，所以由此估算出来的位置信息也会存在有相位延时。

Δθ=arctan（ω/ω_c） （5-101）

修正后的转子位置信息可以表示为

转子速度可以表示为