模型参考自适应系统（Model Reference Adaptive System，MRAS）的思想是采用参考模型，在控制过程中，系统不断检测被控系统的状态、性能以及参数，并实时将系统当前的运行指标与期望指标相比较，进而做出决策，通过自适应律来改变控制器的结构与参数，以保证系统运行在其定义的最优状态。模型参考自适应系统设计的关键是自适应律的选取，自适应律的设计通常使用3种方法：①以局部参数最优化理论为基础的设计方法；②以李雅普诺夫稳定性理论为基础的设计方法；③以波波夫（Popov）稳定性理论为基础的设计方法。考虑到设计的模型参考自适应系统的稳定性，设计自适应律通常以波波夫稳定性理论为基础。
一个典型的模型参考自适应系统由参考模型、可调模型和自适应机构3部分组成。从类型来分可以分为并联型、串联型和串并联型。实际建模中使用最多的是并联型模型参考自适应系统。如图5-24所示，参考模型和可调模型具有相同的外部输入激励u（x），而Xm（t）和Xs（t）分别是参考模型和可调模型的状态输出，系统将Xm（t）和Xs（t）比较后得出的误差e（t）输入自适应机构，通过自适应机构去调节可调模型的参数，使Xs（t）快速逼近Xm（t），也就是误差e（t）趋近于零。
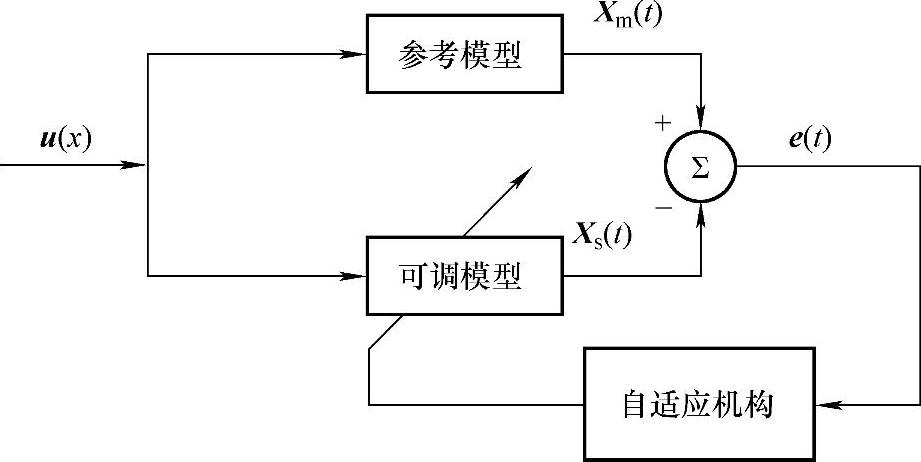
图5-24 模型参考自适应系统控制框图
图5-24所示为并联型模型参考自适应系统控制框图，假设其参考模型的状态方程为
式中，Xm（0）=Xm0，Xm（t）为n维状态向量，u（t）为m维输入向量，Am为n·n维矩阵，Bm为n·m维矩阵。
可调模型的状态方程为
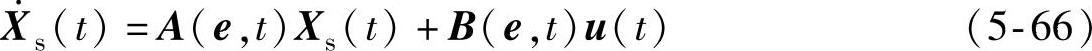
式中，A（e，0）=A0，B（e，0）=B0，Xs（0）=Xs0，Xs（t）为n维状态向量，u（t）为m维输入向量，A（e，t）为n·n维时变矩阵，B（e，t）为n·m维时变矩阵。状态方程系统框图如图5-25所示。
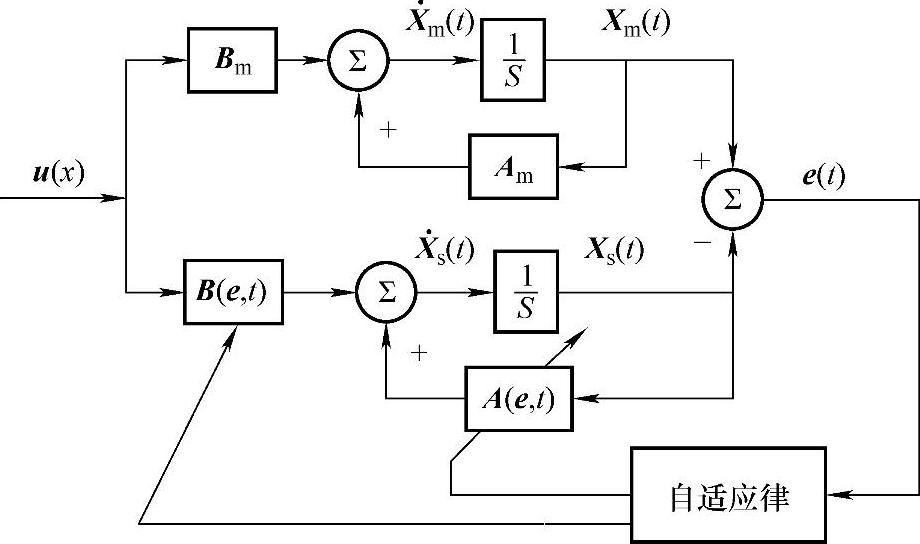
图5-25 状态方程系统框图
系统状态误差为
e（t）=Xm（t）-Xs（t） （5-67）
模型参考自适应系统确立参考模型和可调模型后，设计合适的自适应率，使
，同时可调模型中的矩阵系数应满足
由式（5-65）和式（5-66）可得
式中，η（t）=（A（e，t）-Am）Xs（t）+（B（e，t）-Bm）u（t）。
等价误差系统如图5-26所示，上半部分为线性部分，下半部分为非线性时变部分，当误差e（t）为零时，等价误差系统稳定。在多数情况下，要使前向通道线性部分的传递函数为严格正实函数是很困难的，为此在前向通道上设置了一个线性补偿器D，使e′（t）=De（t），此时线性部分的稳定性取决于Am和D，可通过D来设置线性部分的严格正实性。对于非线性时变部分，当线性部分增加线性补偿器D后，相应的输入要改变。可调矩阵变为A（e′，t）和B（e′，t），相应的可调参数也要改变。在自适应率的作用下，A（e′，t）和B（e′，t）逐渐趋近于Am和Bm，多采用比例-积分器作为自适应率。
根据永磁辅助同步磁阻电机d、q轴数学模型，结合式（5-11）和式（5-12）可以得出d、q轴电流状态方程
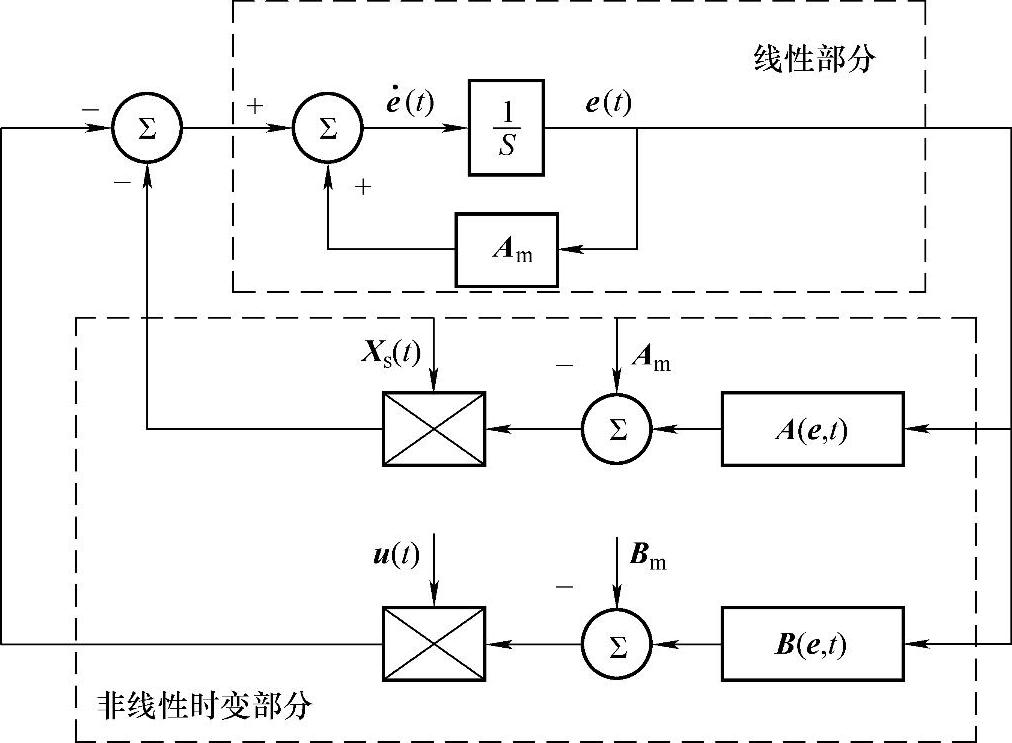
图5-26 等价误差系统
式（5-70）电流状态方程中含有转子速度信息，可选电机本体为参考模型，电流模型为可调模型，对状态仿真稍作处理。
可以得到
式中
根据参考模型可以建立可调模型(www.xing528.com)
式中
根据参考模型和可调模型，定义广义误差为
式（5-71）减去式（5-73）得到
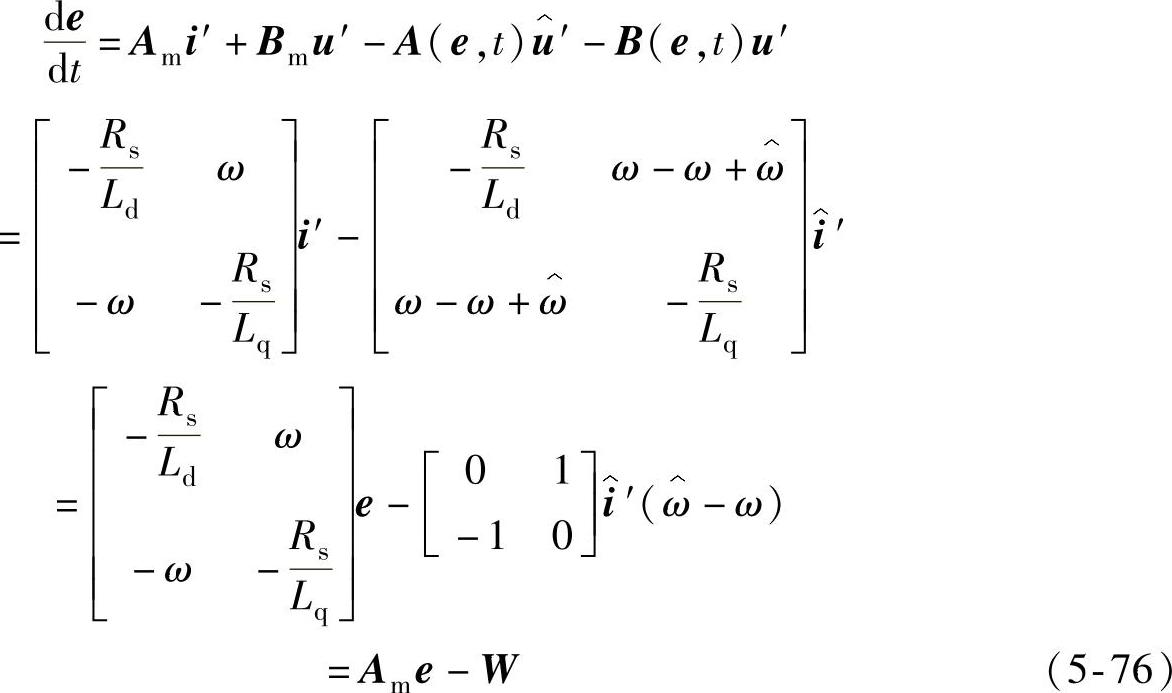
式中，W为
，J为
。
这样就构成了模型参考自适应的反馈系统，如图5-27所示，因为Am正定矩阵的稳定条件只要满足式（5-76），模型参考自适应的反馈系统就是稳定的。
图5-27 模型参考自适应反馈系统
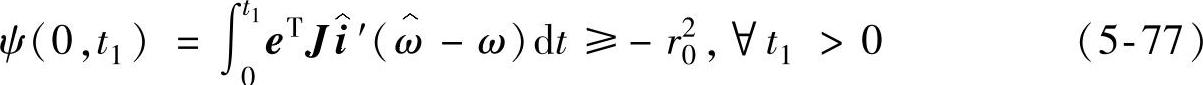
式中，r20是一个有限正数。
要满足式（5-77），通常采用比例-积分器作为自适应率。
式中，
为初始值，将式（5-78）代入式（5-77）得到
要使ψ（0，t1）≥-r20，可以分别使
式中，r21和r22分别为有限的正数，对于任意函数f（t），都会存在以下不等式：
这里假设
对式（5-84）两边求导可以求出
同理可以求出
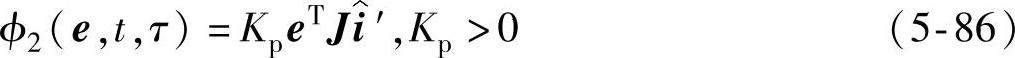
假设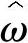
（0）为零，将式（5-85）和式（5-86）代入式（5-78）得到
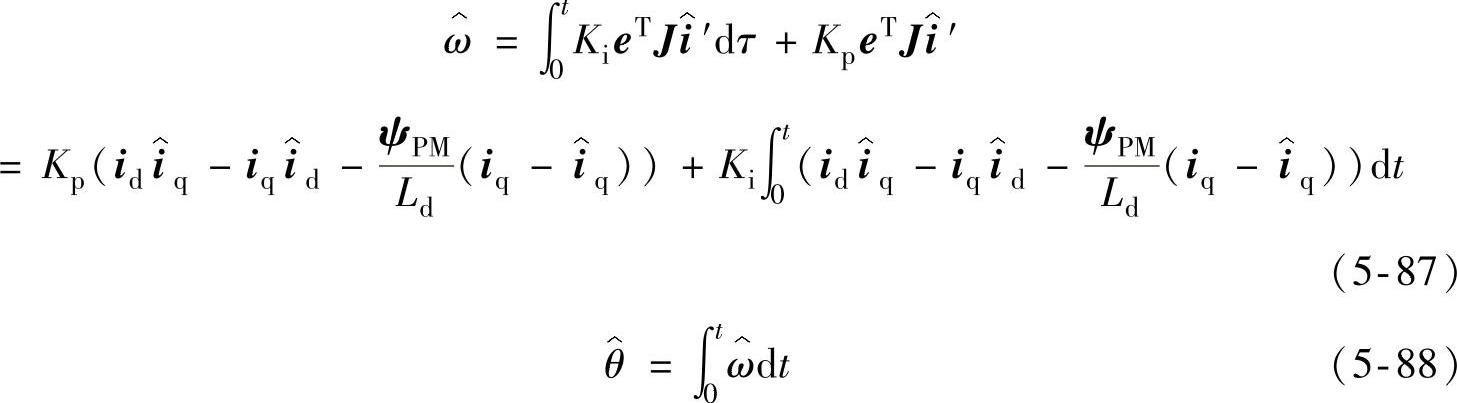
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
