基于优化算法的PID参数整定

数字PID调节器参数的整定，工程上主要借助于积累的调试经验。但是当控制回路较多时，需要整定的PID参数成倍增加，导致整定过程十分麻烦、复杂，甚至不可能实现。

另外，当过程对象特性或参数随着时间、工况改变时，原整定好的PID参数会由于不适应变化了的过程特性和参数，导致使控制性能变差。为使PID参数整定方便快捷，可以利用计算机技术，结合相关优化算法实现这一目标。

1.PID参数自寻优控制需要解决的主要问题

利用计算机快速运算和强大的逻辑判断能力，选定寻优算法，使计算机自动寻找到最优的数字PID调节器参数，使得控制系统性能处于最佳状态。

在PID参数寻优算法中，需要解决的主要问题有：①控制系统性能指标的选择；②寻优算法的选择。

2.性能指标选择

为了直接、客观地达到PID调节器寻优参数的目的，所选的性能指标应当既反映动态性能，又包含稳态特性，选择积分指标才能满足此条件。由于绝对误差积分指标相对容易处理，尤其是误差绝对值乘以时间的积分在计算机中数据容易处理，因此可以选用如下指标：

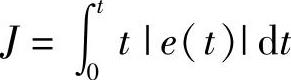
将其离散化得到

采样时间固定时，上式简化为

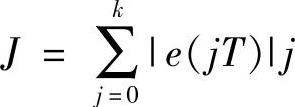
对于一般的控制系统，J经常是极值型函数。最优化理论表明：具有极值特性的函数，在经过有限步搜索以后，一定能够找到极值点。

而为了求得|e（jT）|，从控制系统仿真方式上来看，可以将使用输出值曲线和给定值（一般是一条水平直线）之间阴影部分的面积作为考察的性能指标是合理的；但从实现的角度来讲，计算阴影部分的面积并不容易，所以改为使用每一个时刻的输出值和给定之间的绝对误差的和来充当性能指标，如图5-4-1所示。

另外，除了考虑以任一时刻的输出值和给定值之间的绝对误差之外，还要考虑到控制器的输出，这个值关系到执行器的执行效果，执行器如果不断大幅度振荡显然是不可取的。在具体实现的时候，与前面方法类似，可以将每一时刻执行器的位置差（其实就是PID输出差值）也加入到性能指标里面，达到控制系统性能与执行机构输出性能均最优。

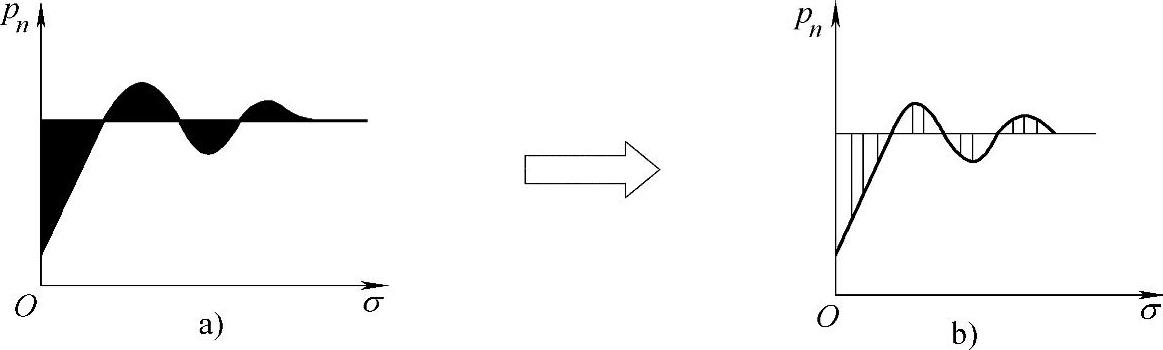
图5-4-1 性能指标选择示意图

a）性能指标为阴影面积之和 b）性能指标为绝对差值之和

3.单纯形寻优法

多参数寻优算法很多，有黄金分割法、插值法、坐标轮换法、步长加速法、方向加速法、单纯形寻优法和随机搜索法等。这其中单纯形寻优法有控制参数收敛快、计算工作量小、简单实用的特点，因此建议使用单纯形寻优法。

所谓单纯形，就是在一定的空间中的最简单的图形。N维的单纯形，就是N+1个顶点组成的图形。如二维空间，单纯形就是三角形。设二元函数J（X₁，X₂）构成二维空间，有不在一条直线上的三个点X_h、X_g、X_l构成另外一个单纯形。由三个顶点计算出相应的函数值J_h、J_g、J_l。若J_h>J_g>J_l，对于求极小值问题来说，当然是J_h最差，J_g次之，J_l最好。

函数变化的趋势是：一般情况下，好点在差点对称位置的可能性比较大，因此将X_gX_l的中点X_f与X_h连接，并在X_hX_f的射线方向上取X_r，使X_hX_f=X_fX_r，如图5-4-2所示。

以X_r作为计算点，计算X_r的函数J_r步骤：

1）当J_r≥J_g时，说明步长太大，以致X_r并不比X_h好多少，因此需要压缩步长，可在X_r与X_h间另选新点X_s。

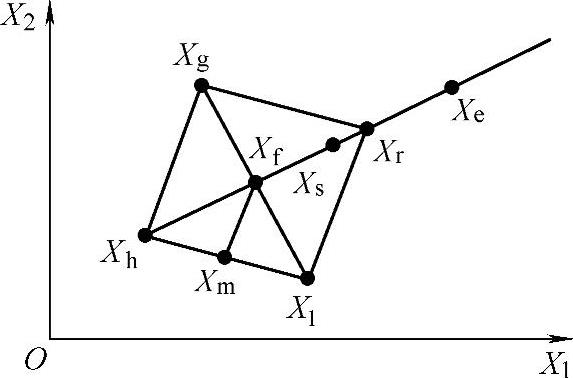
图5-4-2 单纯形算法原理图

2）当J_r<J_g时，说明情况好转，而且可以加大步长，可以在X_hX_r的延长线上取到新点X_e。再计算J_e，若J_e<J_r，取X_e为新点X_s；否则，选X_r作为新点X_s。

3）通过1）、2）计算后可以得到新点X_s。若J_s<J_g，说明情况确有改善，可舍弃原来的X_h点，而以X_g、X_l、X_s三点构成新的单纯形（X_gX_lX_s），称作单纯形扩张，然后重复上述步骤。若J_s≥J_g，说明X_s代替X_h改善并不大，可把原来的单纯形（X_fX_lX_m）按照一定的比例缩小，例如边长都缩小到原来的一半，构成新的单纯形（X_fX_lX_m），称为单纯形收缩。同样重复以上步骤，直到满足给定的收敛条件为止。根据以上的单纯形算法原理及实现步骤，就可以通过软件编程实现其具体应用。

4.具体实现实例

使用单纯形算法整定PID参数时，第一步工作是建立一个控制系统的仿真模型，为方便说明，先用一个典型的单回路控制系统策略为例，其他复杂控制策略方法是类似的。

（1）单回路控制系统仿真模型

图5-4-3为单回路控制系统仿真模型，将PID调节器的三个参数p、i、d（选定PID表达式为p+i/s+d·s）看做单纯形的每一个点的三个元素，J即为它们的性能指标。利用C++进行软件设计，为充分利用C++面向对象的这一特性，可以将PID环节以及传递函数环节用双线性变换法离散成一个个可以直接调用的“函数”，以库文件（PidMod.lib）的形式保存下来，方便后面的直接调用。

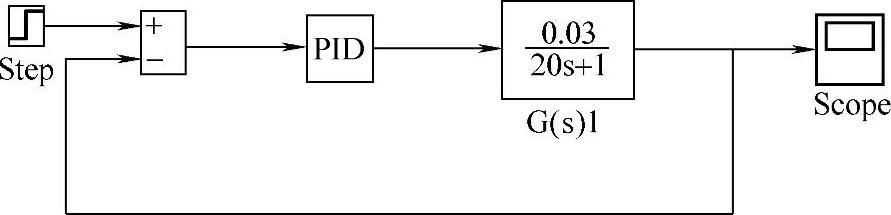
图5-4-3 单回路控制系统结构图

为了计算J，设计了Index函数，在此，函数的实现为

将PID的三个参数作为函数入口参数，iStep为仿真的计算总步数。这样，每一次有新的p、i、d参数就将整个控制系统过渡过程的指标函数计算一次，得到一个指标，即定义的单纯形指标，用于判断下一个点。

因为单纯形的每个点和点之间是相互关联的，而一个点带着PID的三个参数，为方便软件设计，可以使用数组。

在寻优程序运行之初，有数组a，有一个点（p，i，d），由它产生两个新的点，并将数组填充满。

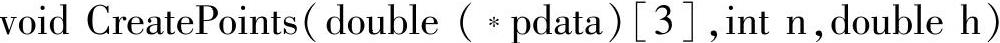(www.xing528.com)

对数组a里面的三个点进行比较，确定X_g、X_l、X_h。生成一个新的数组lgh。在本示例程序中，数组元素存放的顺序对应数组名，以方便后面的调用。

这样就得到了数组lgh，里面是单纯形的三个点。再继续按照前面叙述的单纯形寻优的原理，从该单纯形得到一个新的单纯形（不论它是扩张还是收缩），而这个新的单纯形也就是下一次循环的起点——数组a。

不断地重复以上步骤，就可以得到理想的PID参数值，达到寻优的目的。

例如，设置初始PID参数为（6，2，0），寻优后得到的PID参数为（47.3，2.67，0.0027），利用Matlab进行验证，对比效果如图5-4-4和图5-4-5所示。其中图5-4-4为PID优化前系统响应输出曲线，图5-4-5为PID优化后系统响应输出曲线。可以看出，利用优化算法后控制系统输出响应改善效果十分明显。提醒读者注意的是，PID的表达式在不同情况下是不一样的。例如：

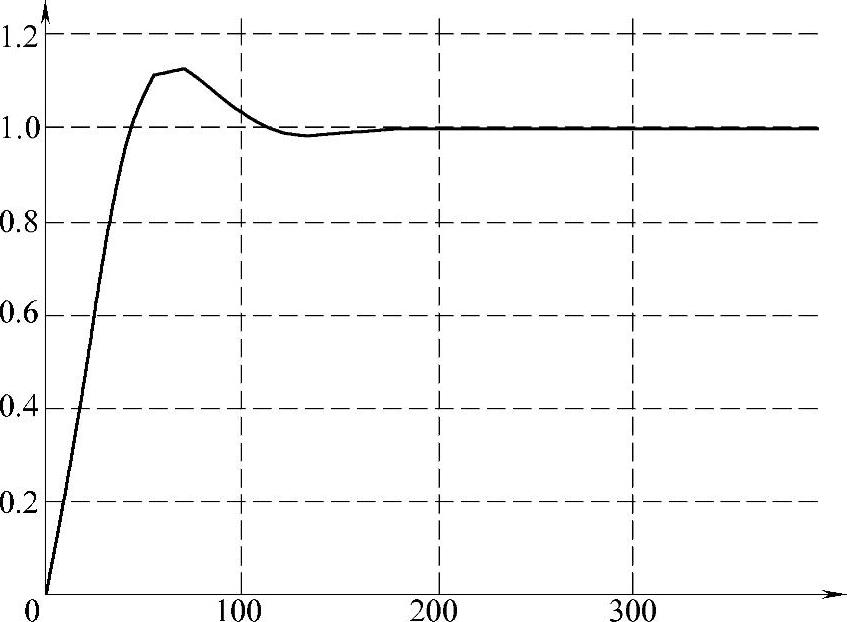
图5-4-4 PID优化前系统响应

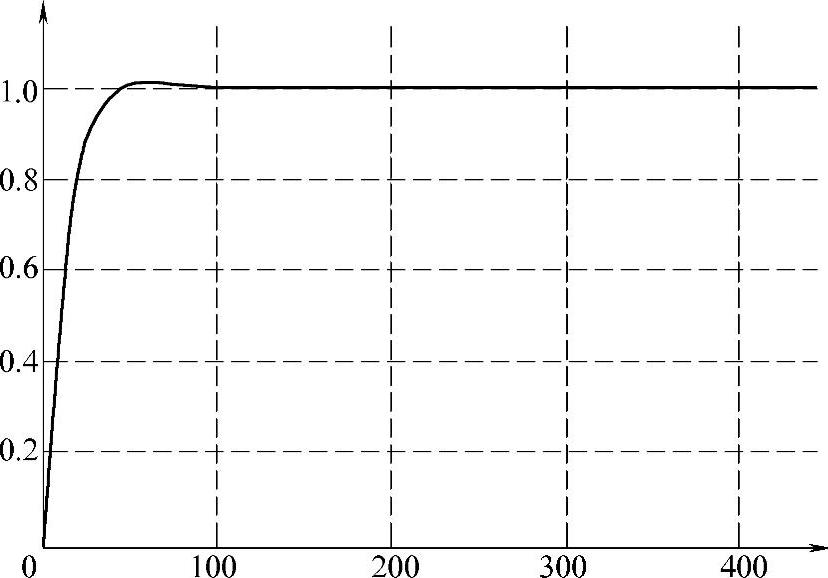
图5-4-5 PID优化后系统响应

Matlab中的PID表达式为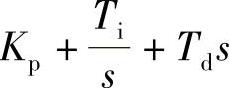，一些习惯的PID表达式为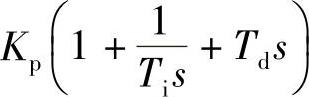。在

优化系统PID参数时不要混淆这些参数。

（2）复杂控制系统仿真模型

以热电站母管制锅炉机组为例，其特点是每台炉的对流及辐射过热器分别设置在左右两侧，在出口处混合联箱汇聚后送入母管供给汽轮机工作，过程如图5-4-6所示。

要求控制系统不仅混合联箱过热汽温达到设定值540℃，而且左右侧过热汽温管道不能有较大温差，否则会严重影响安全机组运行。针对以上特点，设计控制系统结构图如图5-4-7所示，显然这是串级控制结构的变形应用，图中为a甲侧主汽温过程的导前汽温，b为乙侧主汽温过程的导前汽温，c为乙侧主汽温过程的混合联箱出口汽温，也就是要控制的系统输出响应。

从控制系统结构图5-4-7可以看出，有三个PID共九个参数需要整定，难度很大，仅靠经验法或试凑法几乎是不可能的，为此使用前面介绍的计算机优化算法（单纯形算法）进行自动寻优。

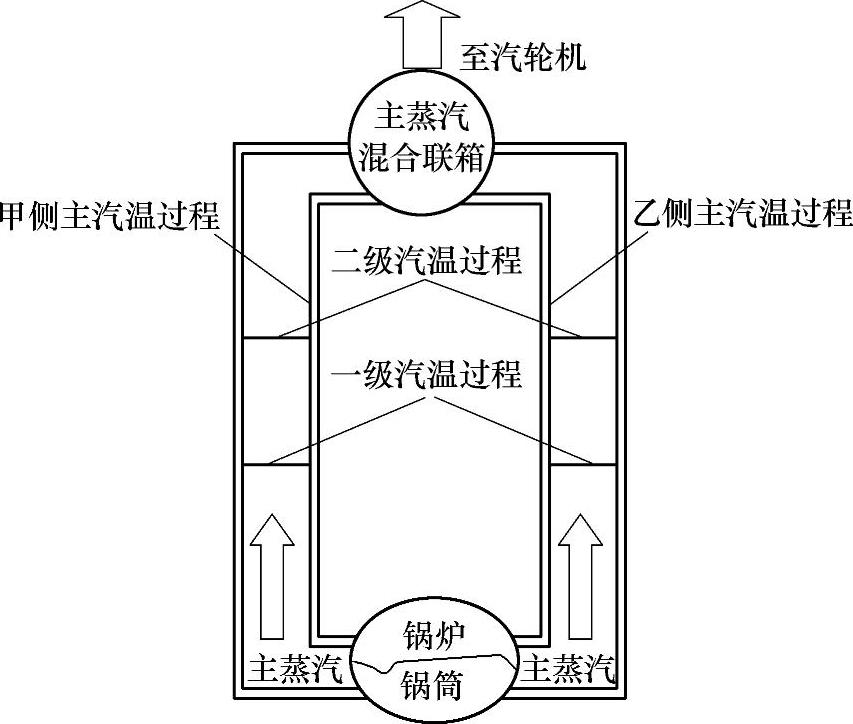
图5-4-6 母管式锅炉汽温过程示意图

假定过程模型参数如图5-4-7所示，PID表达式为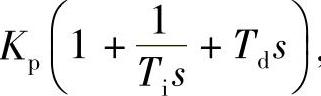，离散化周期为2s，取三个PID初值如下（参见图5-4-7）：

PID1：K_p=5.0，T_i=10.0，T_ds=1.0；

PID2：K_p=1.0，T_i=10.0，T_ds=1.0；

PID3：K_p=1.0，T_i=10.0，T_ds=1.0。

图5-4-7 母管式锅炉汽温过程控制系统结构图

其对应的控制系统响应曲线如图5-4-8所示。从图中可以看出，无论是系统响应还是控制机构输出特性均是不理想的。

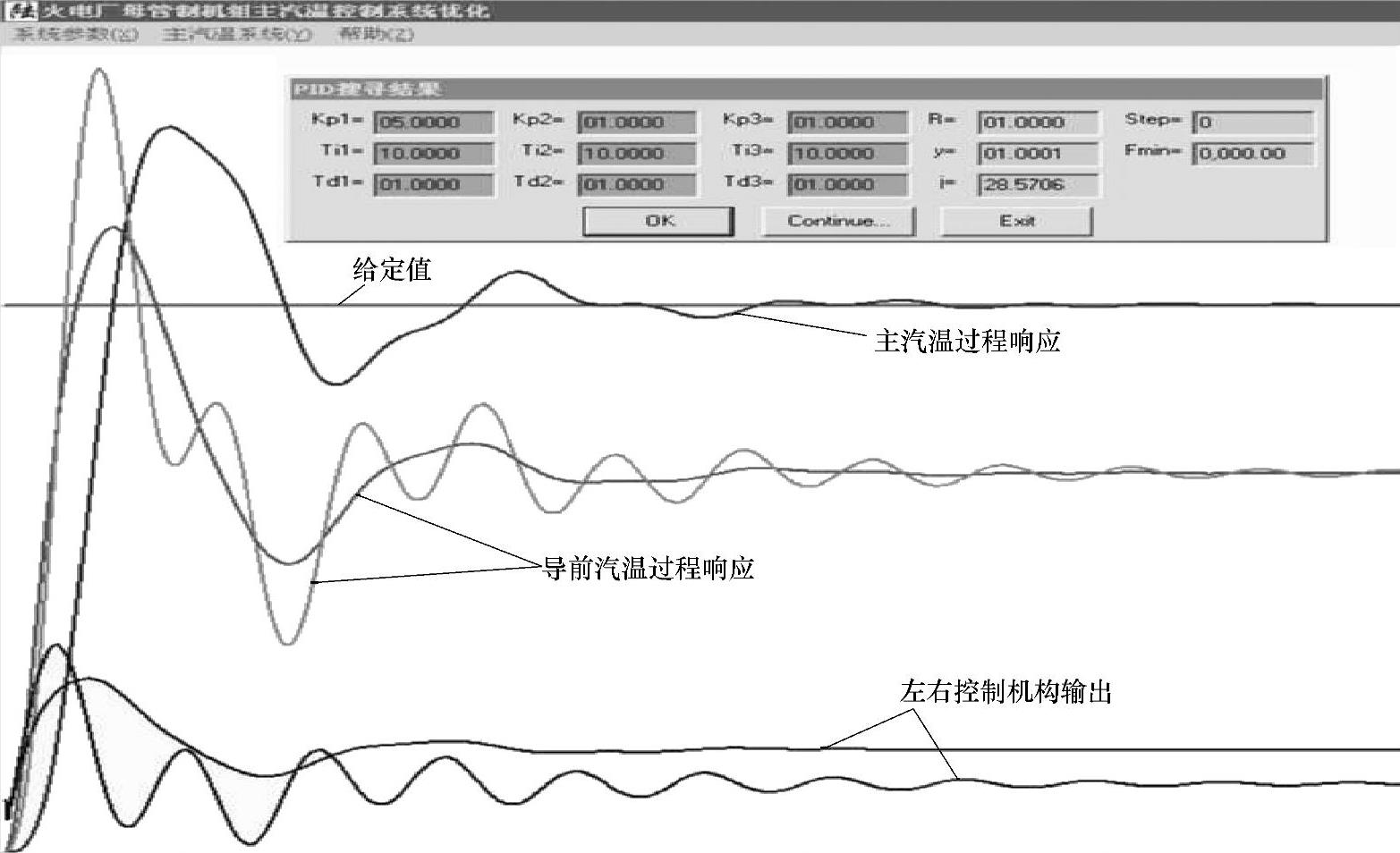
图5-4-8 三个PID参数优化前系统响应

启动单纯形算法进行优化后，得到最佳三个PID参数如下（参见图5-4-9）：

PID1：K_p=9.97，T_i=43.69，T_ds=0.0012；

PID2：K_p=0.81，T_i=11.70，T_ds=0.15；

PID3：K_p=0.97，T_i=32.66，T_ds=0.36。

其对应的控制系统响应曲线如图5-4-9所示。从图中可以看出，无论是系统响应还是控制机构输出特性均得到大幅改善，达到了预期的控制效果，感兴趣的读者可以在Matlab上进行验证系统优化前后的对比结果。

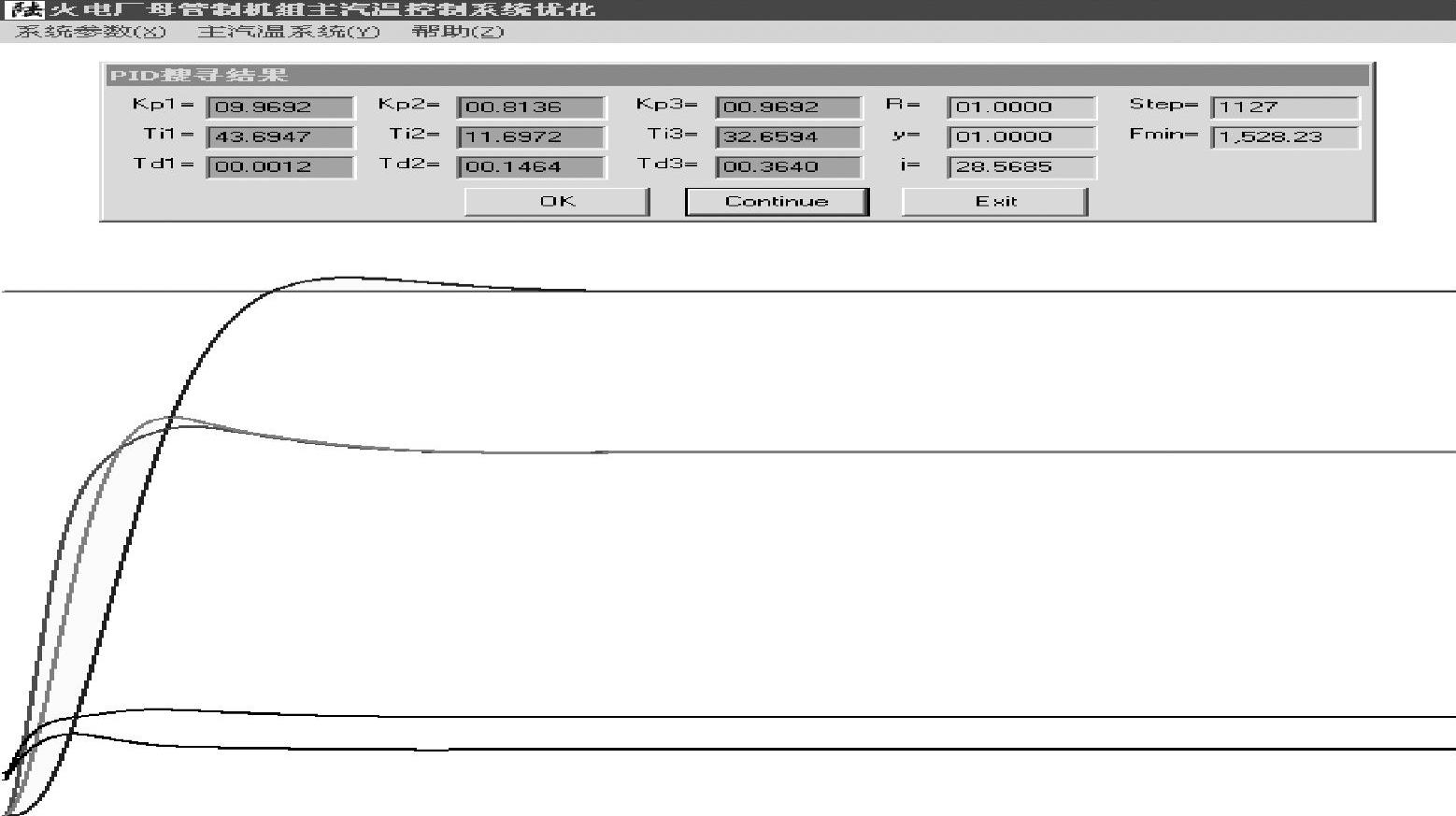
图5-4-9 三个PID参数优化后系统响应

提醒注意的是，使用的PID表达式为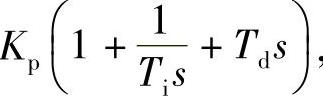而在Matlab中PID的表达式为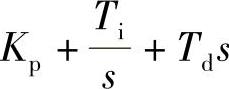，用Matlab验证时要注意转换。

使用单纯形算法寻优PID参数，具有计算量较少、收敛速度快、可以对多个PID参数同时进行优化的特点，并且可以根据不同的限制条件在程序中方便地进行处理，因而，单纯形算法在工程应用中具有重要意义。基于上述原因，一个优秀工程师应该很好掌握并在控制系统设计中做到熟练应用。

最后需要明确的是，PID最佳整定参数确定后，并不能说明它永远都是最佳的，当由于各种外界条件发生根本性改变时，就必须重新根据需要再进行最佳参数的整定。这也是保证PID控制始终有效的重要环节。