如何实现积分分离PID控制？

在连续生产过程中，数字控制的基本控制方式仍采用PID控制规律，因为PID控制是连续系统理论中技术成熟、应用广泛的一种控制方式。它适用于很多场合，特别是对于大多数工业对象，当不准确知道其数学模型时，可以很方便地使用PID调节器。PID参数的调整经过多年的实践已形成一套成熟的经验调试方法，并已为广大工程技术人员和操作人员所掌握。PID控制规律在计算机中也很容易实现，只要根据PID算式编制出程序，就可在计算机上执行。

1.PID控制算式的基本形式

数字调节中的PID控制算式是将PID的模拟表达式进行离散化而得到的。PID的模拟表达式为

式中 p——调节器的输出信号；

e——调节器的偏差输入信号，是测量值m与给定值r之差，e=r-m；K_p、T_i、Td——调节器的比例系数、积分时间常数、微分时间常数。

因为采样周期T_s相对于信号变化周期是很小的，这样可用矩形法计算积分，用向后差分代替微分，则式（5-3-1）中的积分项和微分项可近似表示为

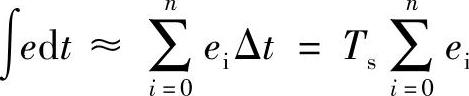
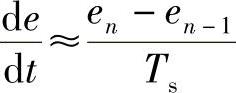
式（5-3-1）便变成了离散PID算式

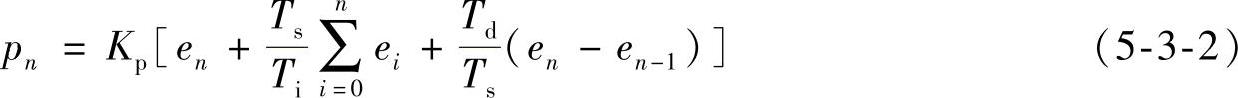
式中 Δt——采样周期，Δt=T_s；

p_n——第n次采样时调节器的输出；

e_n——第n次采样的偏差值e_n=r-m_n；

n——采样序号。

式（5-3-2）为位置式算式，其计算出的输出量与执行机构的位置相对应。

由式（5-3-2）同样可列出第（n-1）次采样的输出表达式

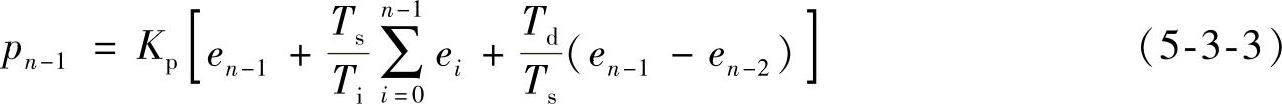
由式（5-3-2）减去式（5-3-3），可得PID调节器输出增量的表达式

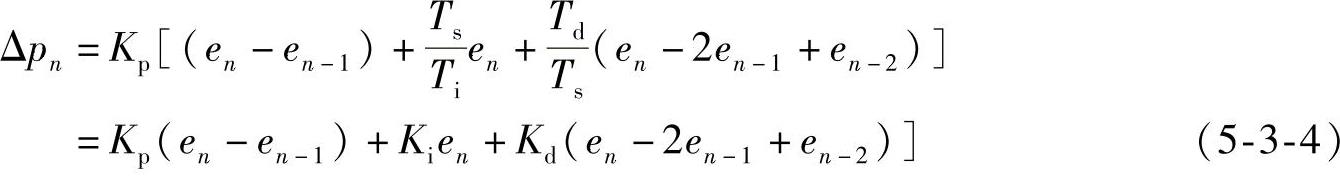
式中 K_i——PID控制算式的积分系数，；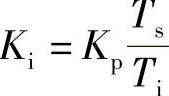

K_d——PID控制算式的微分系数，。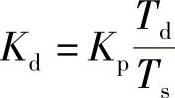

式（5-3-4）运算结果Δp_n表示了执行机构（阀门）位置应改变的增量，为增量式算式。

式（5-3-2）和式（5-3-4）两种控制算式在本质上并无多少区别，只不过在用位置式算式时，p_n=∫Δp_i的任务由软件完成，而在用增量式控制算式时，则需由硬件中的输出通道来完成。两种算式在本质上是一样的，但增量式算式却有一些优点，使它的应用更广泛。这些优点主要有：

1）计算机只输出控制增量，即执行机构位置的变化部分，误动作时影响小。必要时通过逻辑判断进行保护，不会严重影响系统状态。

2）易于实现手动←→自动的无扰切换。

2.实际控制系统中PID算法的不同改进形式

为了改善控制质量，针对不同对象，PID控制中引入了许多新内容，下面予以简单说明。

（1）不完全微分形式

微分作用的引入与模拟调节时作用相同，使系统相位超前而改善控制性能。但数字控制系统中，式（5-3-2）中的理想（完全）微分作用存在以下两个问题：

1）理想微分只在偏差变化瞬时有输出信号，微分作用很弱，控制效果不好，而非理想微分作用时间较长，可加强对过程的控制。

2）当瞬时偏差变化较大时，在一个采样周期内理想微分输出数值可能很大，引起计算机数据溢出。同时，理想微分抗干扰能力很差。

为了防止抗干扰性能恶化，又使微分作用有效，可采用非理想微分的PID控制算式，其传递函数为

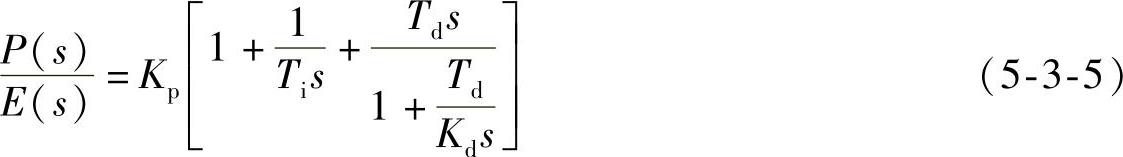
式中 P（s）——调节器输出量的拉氏变换；

E（s）——偏差输入信号的拉氏变换。

将上式分为两部分，即

P（s）=P_PI（s）+P_D（s）式中(www.xing528.com)

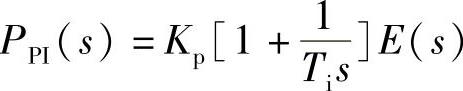
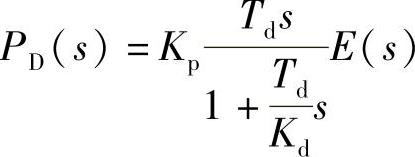
P_PI（s）的差分算式与式（5-3-2）的PI部分相同，即

求P_D（s）的差分算式，首先将其化为微分方程式，即

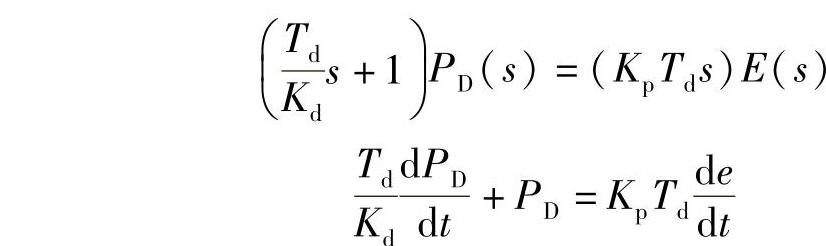
用向后差分代替微分项，则在第n次采样时，有

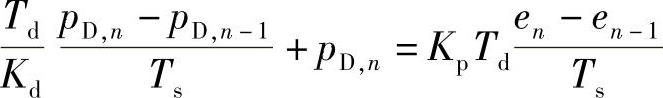
化简上式

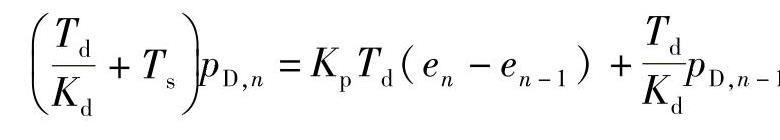
所以

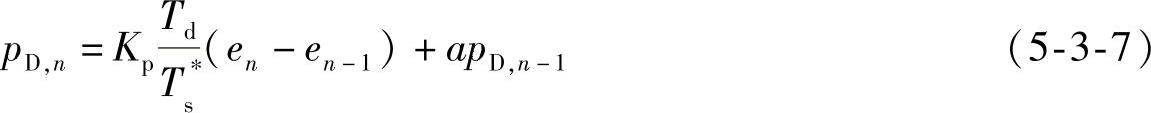
式中

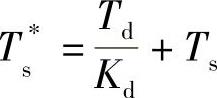
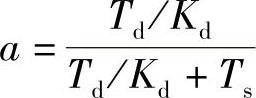
将式（5-3-6）与式（5-3-7）合并，可得非理想微分的PID控制算式

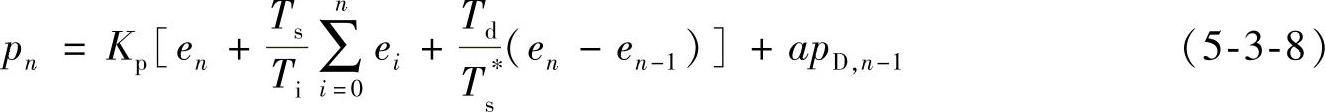
它与理想微分的PID控制算式相比，多一项n-1次采样的微分输出量αp_D，n-1。在单位阶跃偏差作用下，它们输出特性的差异如图5-3-1所示。

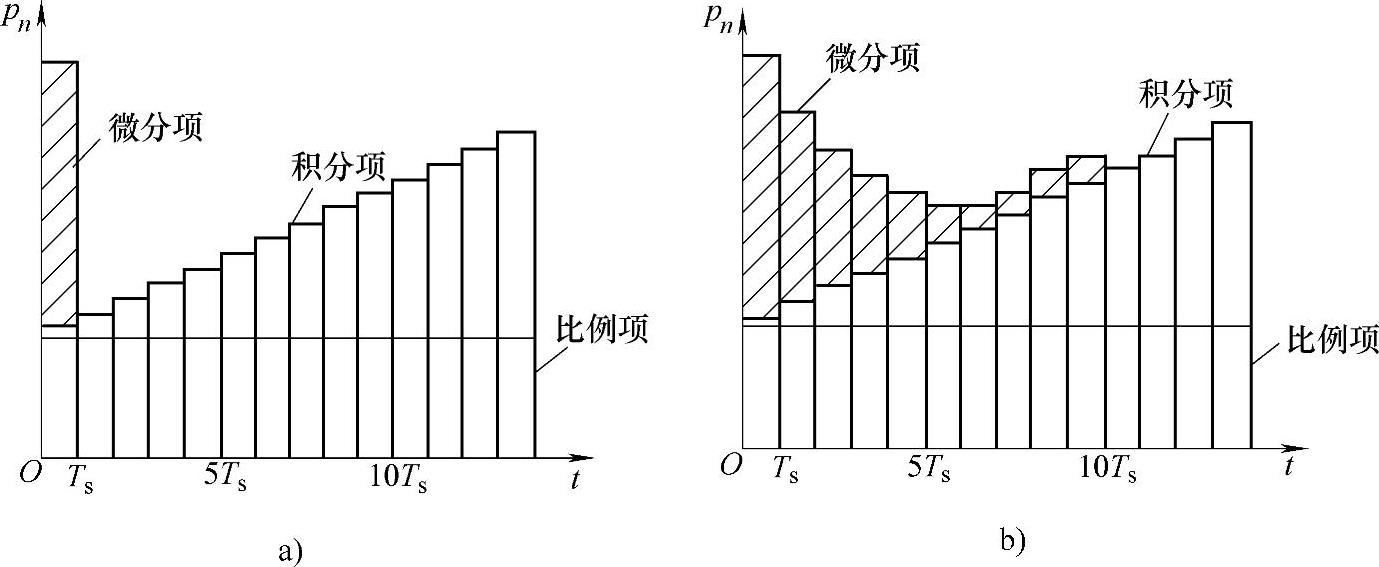
图5-3-1 PID控制算式的输出特性

a）理想微分式 b）非理想微分式

（2）微分先行PID控制模式

微分先行PID的结构如图5-3-2所示。

这是一个PD与PI的串联结构，它只对测量值M进行微分，而不是对偏差进行微分，这样在给定值R变化时，不会产生输出的大幅度变化，即可避免给定值扰动，这种算式适用于给定值R经常变化的情况。

（3）积分分离PID控制

对一般的PID控制算式，当开工、停工或大幅度提降给定值时，由于短时间内产生很大偏差，往往会出现严重的积分饱和现象，以致造成很大的超调和长时间的振荡。为了克服这一缺点，可采用积分分离算法，即在偏差大于一定值时，取消积分作用，而当偏差小于这一值时，才将积分引入。这样既可减小超调，又可达到积分校正的效果，即可以消除偏差。

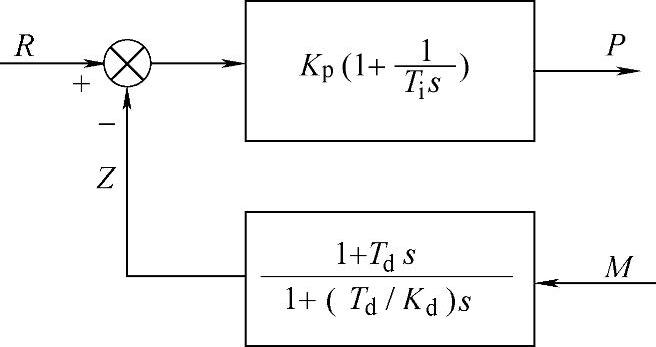
图5-3-2 微分先行PID的结构图

积分分离的PID算法为

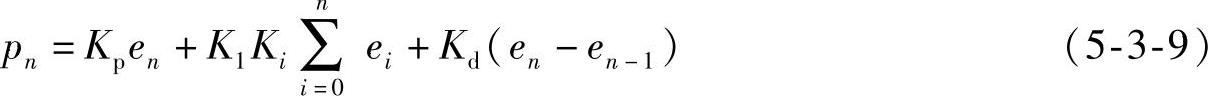
式中

K_l称为逻辑系数，A为预定门限值，显然当e>A时，积分不起作用，只有当偏差e≤A时，积分才引入。在积分分离的PID算法中，也可用增量式算式。

（4）带有死区的PID控制

带有死区的PID算式为

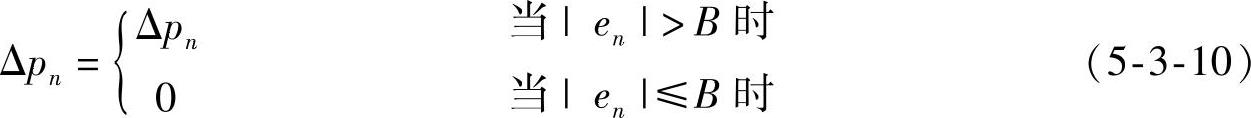
当偏差绝对值|e_n|≤B时，本次不进行计算和输出，即本次输出Δp_n=0；当偏差绝对值|e_n|>B时，进行PID运算，计算结果p_n作为本次输出。这种控制方式适用于控制准确度要求不太高，但要求控制作用尽可能少变化的场合，如中间容器的液面控制。