材料力学性能力学性能出现方向性

1.力学性能出现方向性

冷挤压时，金属朝着一定方向流动。因此，冷挤压后，挤压件的力学性能出现了方向性，与流线方向相垂直和平行的方向上的强度是不同的，如图1-63所示。

2.硬度分布不一致

冷挤压时，因各部分的变形程度不同，使其各部分的硬化程度有较大的差异，这些差异可以用各处的硬度分布来表示。图1-64所示为45钢正挤压与镦挤压成形后的硬度分布。由该图可知，除了强烈的镦挤压部分以外，其余部分的表层比心部的加工硬化程度都要大。

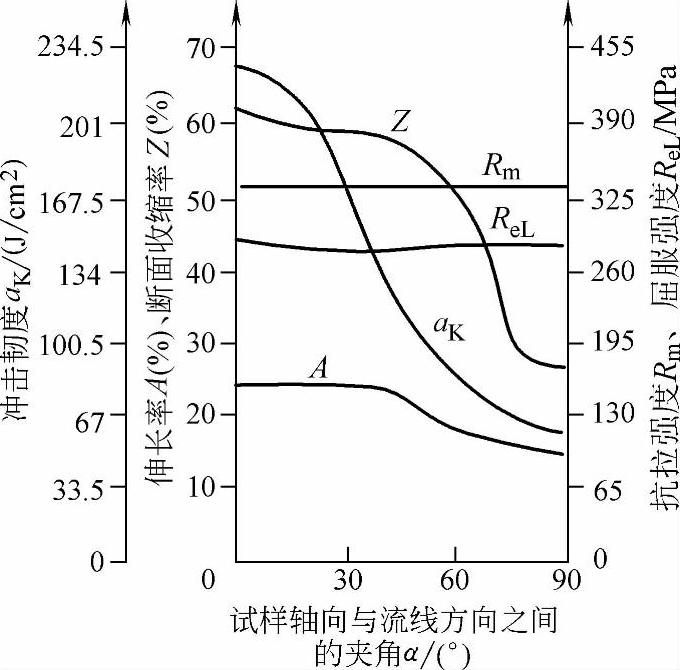
图1-63 力学性能与流线方向的关系

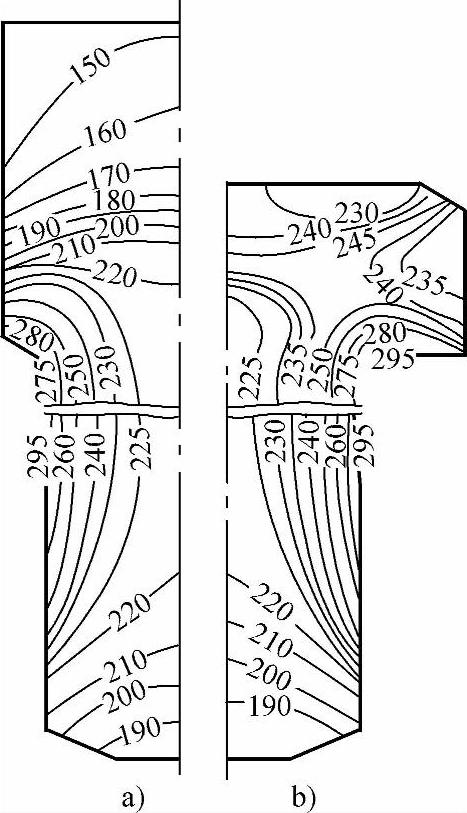
图1-64 45钢正挤压与镦挤压成形后的硬度分布

a）正挤压成形 b）镦挤压成形

3.力学性能的变化

1）正挤压杆形件由于塑性变形伴随着金属强化，材料的抗拉强度、屈服强度以及硬度都随变形程度增加而提高。图1-65和图1-66分别表示出了变形程度与抗拉强度和硬度的关系。

由图1-65可知，R_m与ε_F呈线性关系，因此可用下式表示

R_m=（400+4ε_F）K （1-14）

式中的K为材料系数，可由表1-2查得。

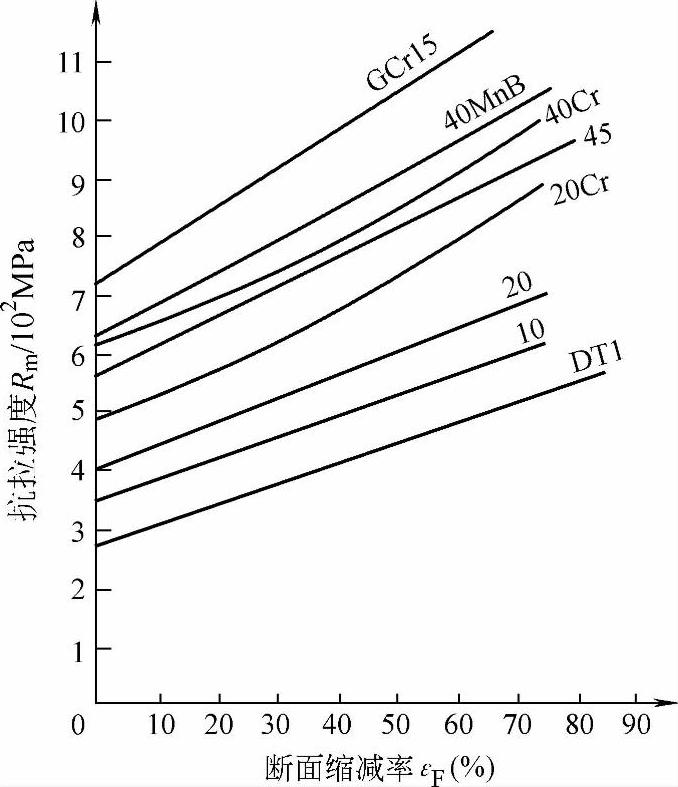
图1-65 正挤压时不同材料的R_m与ε_F的关系

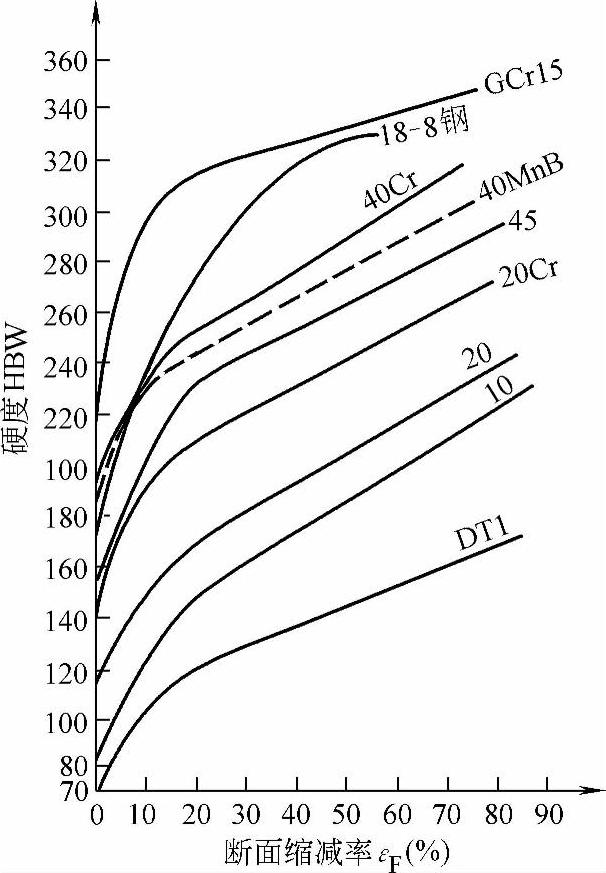
图1-66 正挤压时不同材料的布氏硬度HBW与ε_F的关系

表1-2 材料系数K

通过分析图1-65与图1-66可知，R_m、HBW皆随ε_F呈线性关系增加，因此可求得R_m与HBW的关系式

式中 HBW——正挤杆件中心部分的硬度；

R_m——正挤杆件中心部分的抗拉强度（MPa）；

K_F——材料系数，由表1-3查得。

表1-3 材料系数KF

(www.xing528.com)

伸长率A、断面收缩率Z随变形程度增加而下降，如图1-67所示。

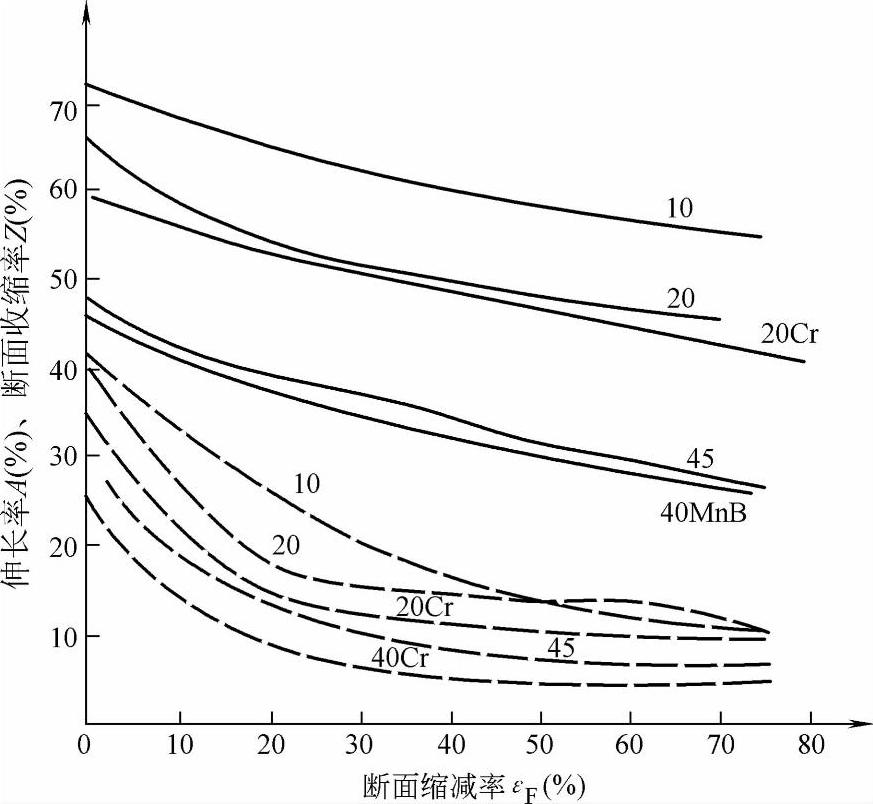
图1-67 正挤压时不同材料的A、Z与ε_F的关系

----伸长率A ——断面收缩率Z

2）反挤压杯形件与正挤压情况基本相同，抗拉强度R_m、维氏硬度HV5随ε_F增加而增加，A、Z随ε_F增加而下降，如图1-68～图1-71所示。

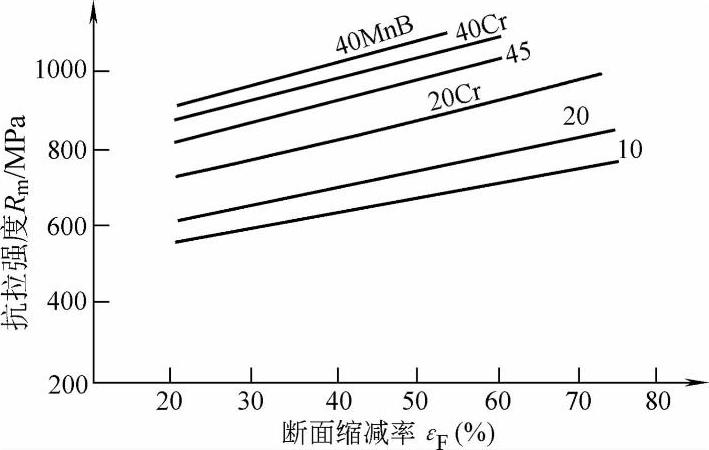
图1-68 反挤压时不同材料的R_m与ε_F的关系

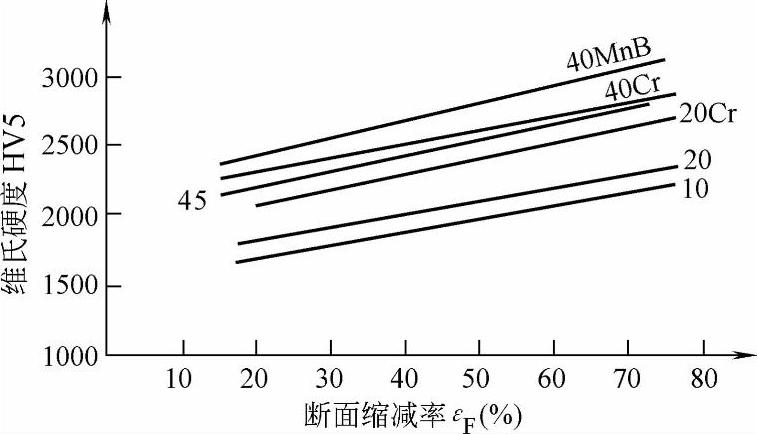
图1-69 各种材料反挤压件外壁维氏硬度HV5与ε_F的关系

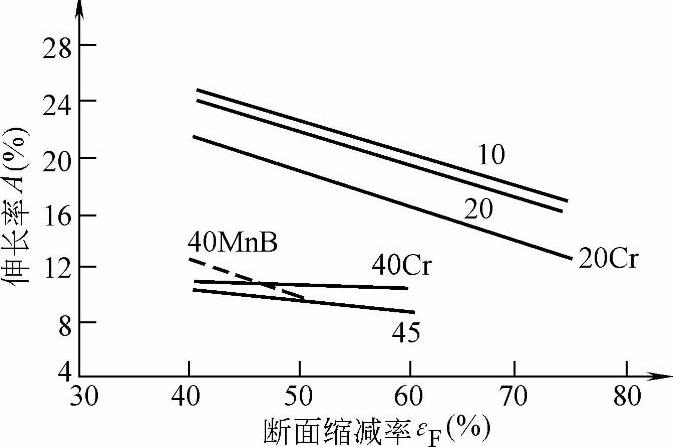
图1-70 反挤压件的伸长率A与ε_F的关系

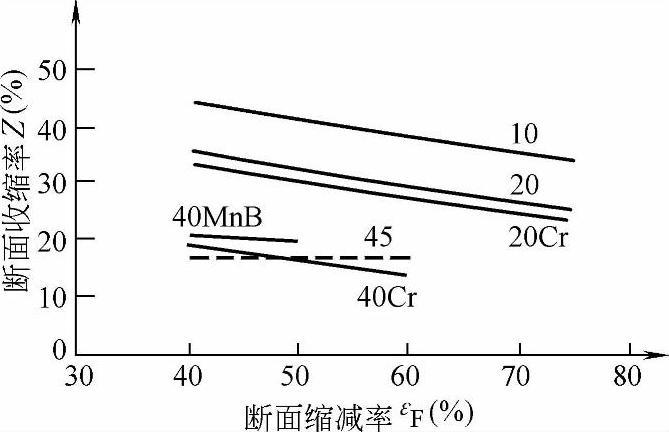
图1-71 反挤压件的断面收缩率Z与ε_F的关系

由图1-68可知，R_m与ε_F呈线性关系。它们的关系可用下式表示

R_m=R_m0+145+Bε_F （1-16）

式中 R_m0——材料原始状态的抗拉强度（MPa）；

B——材料系数，可由表1-4查得。

表1-4 材料系数B

分析图1-68与图1-69可知，R_m、HV5皆随ε_F呈线性关系增加，因此R_m与HV5关系式为

式中 R_m——挤压件的抗拉强度（MPa）；

HV5——挤压件外壁维氏硬度（采用50N试验力）；

K_b——材料系数，可由表1-5查得。

表1-5 材料系数Kb