【摘要】：故障飞机进入维修站后如果有空闲的维修设备则直接进入维修流程，否则进入等待队列。研究维修设备服务过程一般用到排队论。设维修设备的维修速率均为μ，维修的排队模型如图8-24所示。系统的状态转移图如图8-25所示，图中，状态名称为系统中总共送修的设备。
故障飞机进入维修站后如果有空闲的维修设备则直接进入维修流程，否则进入等待队列。等待队列接受维修服务一般按照先到先服务原则（First Come First Seruce，FCFS）进行。研究维修设备服务过程一般用到排队论。
根据假设，设备到达率为故障率λ，设备修复速率为μ，此维修系统属于单件送修多服务台排队系统，记作：
[M|M|N]：[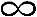
|
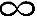|FCFS] （8-73）
式中，第一个M表示送修的故障产品间隔时间服从指数分布；第二个M表示维修设备服务时间服从指数分布；N表示危需设备数量；第一个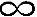
表示维修站排队系统的容量是无限的；第二个
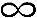表示可能的故障产品可以为无限多。
设维修设备的维修速率均为μ，维修的排队模型如图8-24所示。系统的状态转移图如图8-25所示，图中，状态名称为系统中总共送修的设备。
由生灭过程理论，得到系统的稳定状态概率为
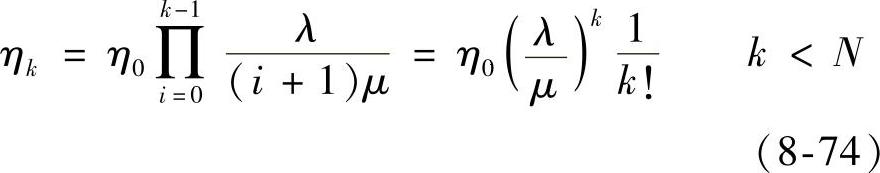
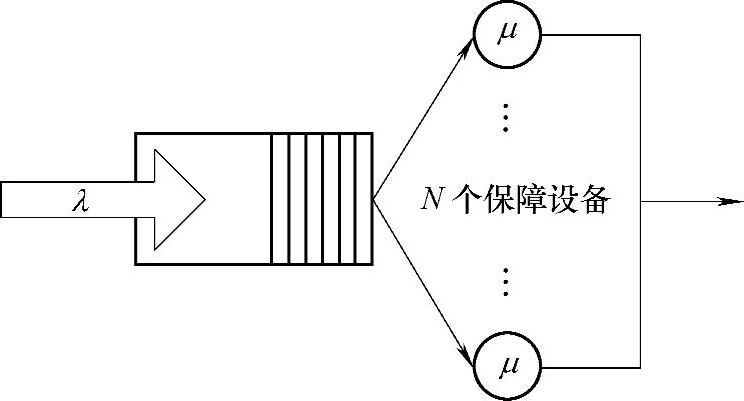
图8-24 维修的排队模型
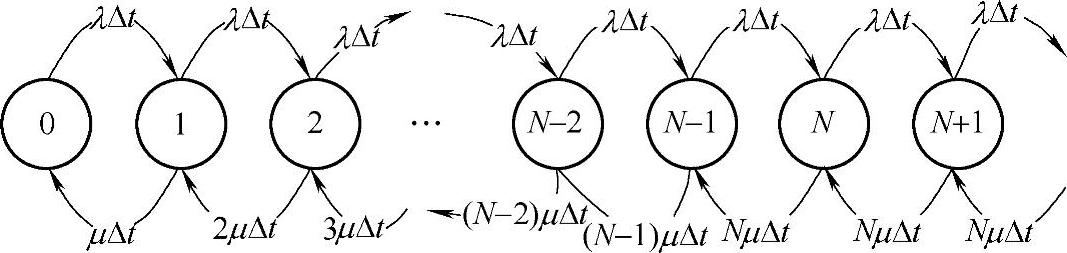
图8-25 系统的状态转移图
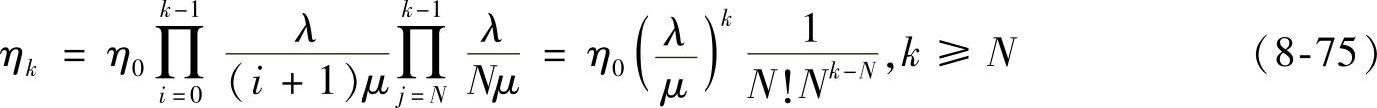
令ρ=λ/Nμ，则稳定条件为ρ＜1，由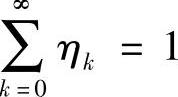
和式（8-75）可得η0表达式为(https://www.xing528.com)
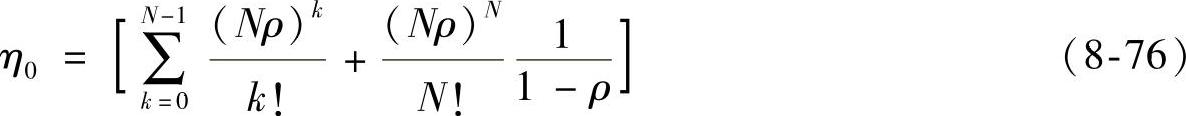
则系统中平均送修备件数量为
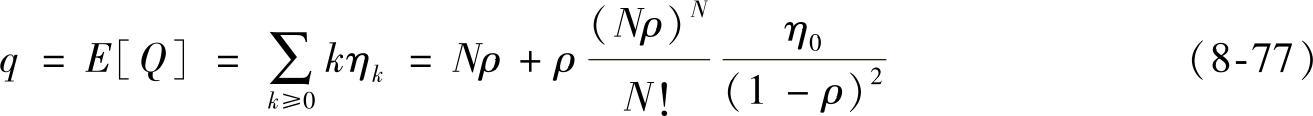
系统中正在工作的保障设备数为M的概率可由式（8-78）表示：
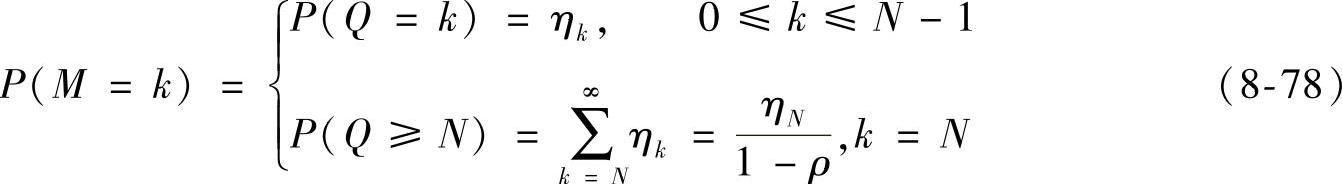
平均正在工作的保障设备数量：
所有维修保障设备均被使用的概率，即到达的送修飞机处于等待维修状态的概率为
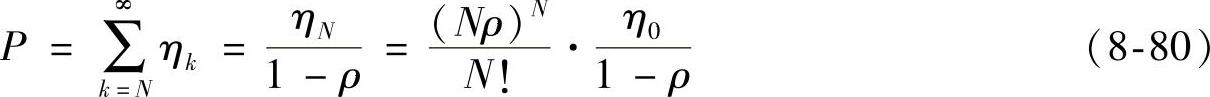
由Little公式可得每个送修件在维修保障系统中花费的时间为
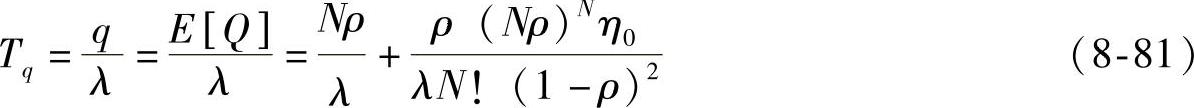
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
