维修任务调度模型A的优化方案

假设现有m个维修小组，n个工作单元。当前工作单位中有s台装备故障，故障装备编号为N_i（i=1，2，3，…，s），将由维修小组x_k（k=1，2，3，…，m）负责维修，在该小组中的任务序号为o_i，所需维修时间为t_i。

当形成调度方案时首先假设以下条件：①所有维修小组的维修能力（包括可维修装备的种类、维修每种装备所需的维修时间，所持有的维修资源等）相同；②每个故障装备只能占用维修小组集合中的一个，且执行过程不能中断；③每个维修小组在任何时候只能同时满足一个故障装备的需求。

确定维修任务分配方案时，要使系统最快得到恢复，一般以单元修复后的时间来衡量，因此维修任务分配方案的目标为最大化全部单元修复后的作战时间。假设第j个单元开始维修的时刻为0，维修结束的时刻为t_e，则维修任务分配问题的目标函数为

max∑ⁿ_j=1（t_e-t_ju） （7-34）

式中，t_ju为当前作战单位的全部故障装备修复的时刻，也可以看做该作战单位的故障装备在维修系统逗留的时间。

式（7-34）所示的目标函数可以转化为

min∑ⁿ_j=1t_ju （7-35）

式中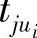，表示第j个单元的第N_i个故障装备的维修所需时间。

假设各维修小组已经分配了一定的维修任务，即目前维修小组x_k的任务所需维修时间为t_gk（k=1，2，…，m），同时，当前的故障装备还没有分配给各维修小组。

为了使得当前单元的故障装备修复时间t_ju最小化，必须使得t_jui最小。把当前单元的故障装备看成一个整体均衡考虑，一种简单的规则是把维修时间t_i最大的故障装备N_i交给t_gk最小的维修小组x_k，直到全部故障装备分配完毕。这种方法可用于产生初始分配方案，故维修任务调度初始方案生成步骤如下（即算法1）所述。

1）输入维修小组数目m，输入当前的故障装备数量s，各故障装备编号N_i及所需维修时间t_i（i=1，2，…，s）；初始化各维修小组当前已分配维修任务的总维修时间t_gk（t_gk初始值为0，且k=1，2，…，m）。(www.xing528.com)

2）所有维修小组中当前已分配维修任务的总时间最小的小组（时间一样时，取出编号最小的小组）的任务时间t_gk和小组编号x_k；

3）当前故障装备中所需维修时间最长的装备的维修时间t_i和装备编号N_i；若t_i≠0，则把故障装备N_i分配给维修小组x_k，t_gk←t_gk+t_i，记录分配关系x_i和N_i，并将故障装备N_i的维修时间t_i清零，即t_i←0，返回步骤2）；若t_i=0，则分配结束，进入步骤4）。

4）并输出调度初始方案。一般而言，采用前述维修调度步骤只能得到近似解。例如假设m=3、s=3，t_g1、t_g2、t_g3分别为0、2、8，t₁、t₂、t₃分别为3、4、5。分配结果为维修小组x₁维修故障装备N₁、N₃，维修小组x₂维修故障装备N₂，最大维修时间为t_ju=max{t_g1+t₁+t₃，t_g2+t₂}=8。然而，若假设维修小组x₁维修故障装备N₁、N₂，维修小组x₂维修故障装备N₃，最大维修时间却为t_ju=7。由此得到一种调整方法。假设初始方案中维修小组x_kmax和_xkmin的已分配的维修时间分别为最大值和最小值，则调整维修小组x_kmax和x_kmin的维修任务，以减少t_ju。初始方案（算法1）调整为以下步骤（即算法2）：

1）分别取出维修小组中x_kmax和x_kmin已分配的维修时间t_gmax和t_gmin。

2）在这两个小组中确定需交换的装备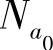、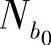，且满足式（7-37）：

式中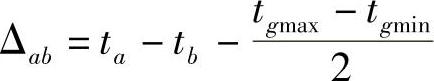，；t_a、t_b分别为小组x_kmax、x_kmin中的装备N_a、N_b的所需维修时间。

3）若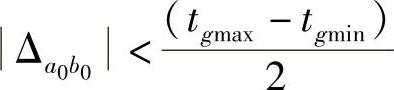，则互换维修小组x_kmax、x_kmin中的故障装备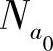、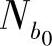，更新相应的t_gk，以及分配关系x_i和N_i，并返回步骤1）；若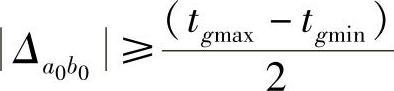，则进入步骤4）。

4）形成最终的维修调度方案。

需要说明的是，由于本章中的管理平台的具体情况对于单个单元，且故障装备种类仅为8种，经试验，最多仅需一次装备交换就可以得到最优解，因此为了提高程序运行效率，此步骤（算法2）不进行循环，仅运行一次。