维修性数学模型的应用和优势

维修性函数表达了规定条件下产品维修概率与时间的关系，是最基本的维修性模型。通常在工程设计中，作为一种工作性的陈述，把维修性视为一种设计系统的固有特性，这种固有的系统特性决定了为把系统维持在或恢复到给定使用状态所需的维修工作量。更确切地讲，维修性就是产品在预定的维修级别上，由具有规定的技术水平的人员，利用规定的程序和资源进行维修时，保持或恢复到规定功能的能力。

（1）维修度M（t） 从维修性的定义可以看出，维修性除与系统的设计有关外，还受维修人员的技术水平、维修程序、维修设施以及维修时所处的环境等因素影响。维修性的特征量也是概率参数，其量化的度量指标是维修度。维修度是表征可修系统维修难易的程度。它的定义为：可维修产品在规定的条件下，在规定的时间内，保持或恢复到规定功能的概率。

维修度M（t）是维修时间Y的分布函数：

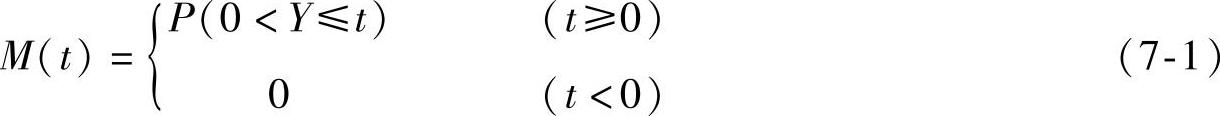
当维修时间Y的维修密度函数m（t）已知时，M（t）可由式（7-2）表示：

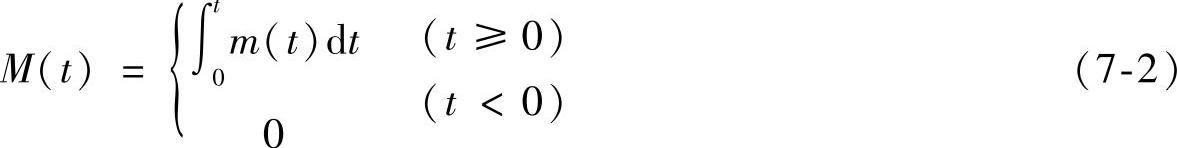
如果M（t）是可微的，则

所以，维修密度函数m（t）是在Δt时间内完成维修的概率。维修密度与维修概率的分布形式有关，随着分布的不同而不同。

（2）维修率μ（t） μ（t）定义为产品在t时刻产品还没有修复的情况下，它在（t，t+Δt）时间间隔内完成维修的条件概率，即

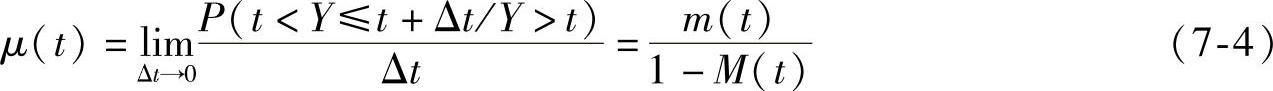
（3）平均维修时间MTTR 平均维修时间MTTR（Mean Time ToRepair）是维修时间Y的数学期望。

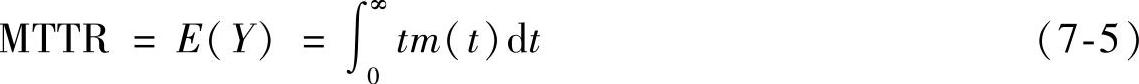
1.MTTR及其时间要素

根据GJB 451—1989《可靠性维修性术语》，MTTR的定义为：在规定的条件下，在规定的时间内，产品在任一规定的维修等级上，修复性维修总时间与该等级上被修复产品的故障总数之比。这个定义可方便地使用于利用维修数据或正式的维修性验证试验，但不便用于维修性预计。在维修性预计中，不能有把握地考虑与使用或后勤有关的时间，也不能准确考虑间歇故障或诱发故障等不可预计的故障发生。为便于维修性预计，MTTR定义为：在所有可预计的非计划维修活动中，完成维修有效时间的概率分布的平均值除以这些非计划维修活动的相对频数。这里采用一般的时间综合来建立MTTR模型，把与维修活动各部分有关的时间加在一起获得该维修活动的总维修时间。应当指出，对每项独立的维修活动而言，所预计或估计的维修时间是为完成该维修活动的平均时间。

MTTR的时间要素按表7-1所示进行分类，其定义见表7-2，表7-2中的缩写在第j个故障隔离结果已知的情况下对第i个RU进行第m项维修活动的时间。

表7-1 MTTR的时间要素

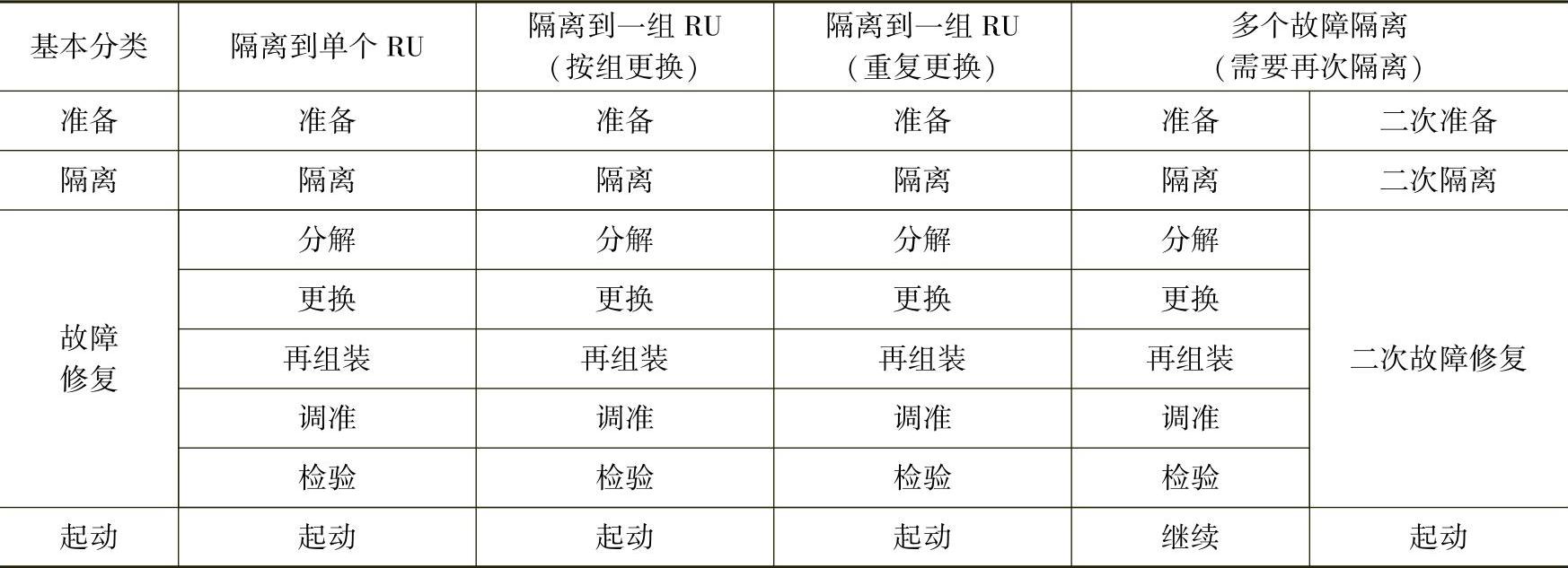
表7-2 MTTR的维修时间要素的定义

2.维修时间的统计分布模型

通常，产品的维修时间不是一个常量，而是以某种统计分布形式存在的概率分布。在维修性分析中，常用对数正态分布、威布尔分布等。

1）威布尔分布适用于简单的维修活动和基本维修作业，如简单地拆卸或更换某个零部件所需的时间一般符合威布尔分布。

2）对数正态分布适合于描述各种复杂装备的维修停用时间，这类时间一般由较多的小的维修活动（如故障判定、故障排除等）组成的。

3）指数分布。一般认为短时间调整或迅速更换即可修复的产品服从指数分布。由于指数分布简单，所以广泛应用于维修分析中。

3.MTTR通用模型

MTTR可由式（7-6）计算：

(www.xing528.com)

式中，N为可更换单元（RU）的数量；λ_i为第i个RU的故障率，不包括任何未检测出故障的故障率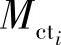；为第i个RU的平均修复时间，可用式（7-7）计算：

式中，K为不同故障隔离结果的数量；λ_ij为第j次故障隔离结果指出的第i个RU中元器件的故障率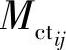；为第j次故障隔离结果指出的第i个RU的平均修复时间，可用式（7-8）计算：

式中，M_ij为当在第i个RU中发生一次故障并产生第j故障隔离结构时完全修复性维修的步数，它包括所有的维修活动：准备、隔离、更换等，也可能包括在第j次故障隔离结构中指出的其他RU上的工作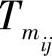；为第j次故障隔离结果指出的第i个RU进行m步修复性维修的平均时间。

4.MTTR专用模型

MTTR专用模型仅适合专门的维修思想，不同的维修思想有不同的专用维修模型。对于采用多种类型的维修活动，必须应用通用模型。

（1）单个隔离模型 单个隔离模型是将故障隔离到单个RU并更换该RU而完成的维修模型，如图7-4所示。

图7-4 故障隔离到单个RU的维修模型

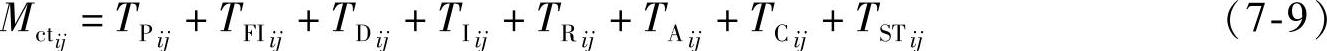
（2）成组隔离模型（1型）—分组更换 通过将故障隔离到一组RU并更换该组所有的RU而进行维修的模型称为成组隔离模型。

1）通用模型（N_j=RU组的数量），如图7-5所示给出了通用分组更换模型。

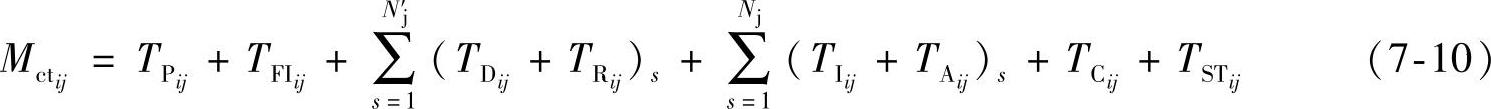
式中，N_j为第j次故障隔离结果必须更换的RU数量；N′_j为第j次故障隔离结果所要求的分解或再组装的次数。如果每次更换要求独立分解和再组装时，N_j=N′_j。

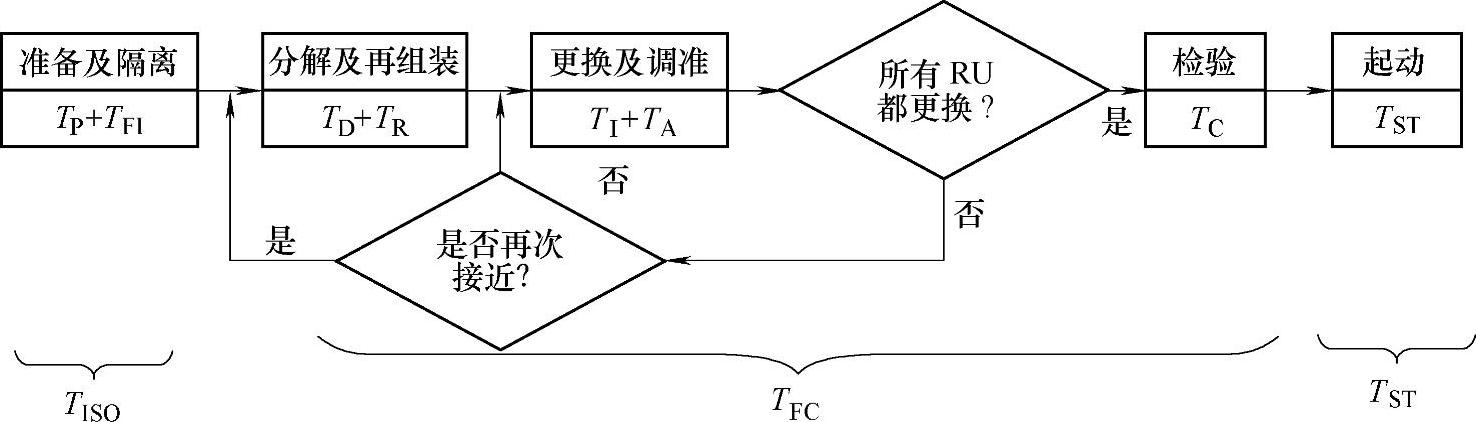
图7-5 通用分组更换模型

2）简化模型（单个接近）。单个接近的简化模型如图7-6所示。

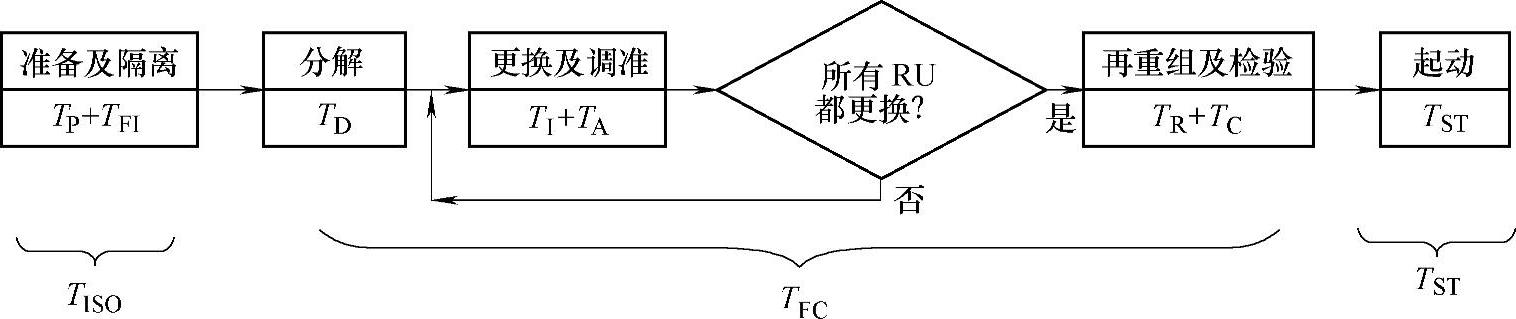
图7-6 单个接近的简化模型

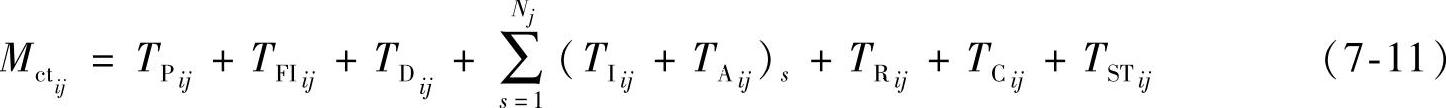
3）成组隔离模型（2型）——重复更换。 将故障隔离到一组RU，并相继更换可能有故障的RU，每次更换1个直到故障修复而进行的维修，如图7-7所示。

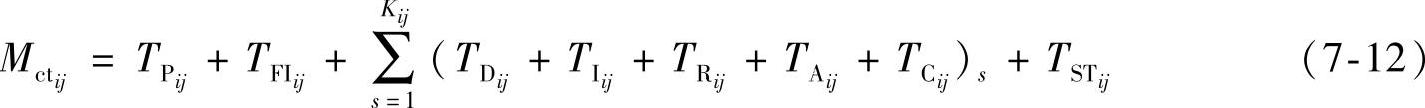
式中，K_ij为第j次故障隔离结果指出的第i个RU的更换次数。

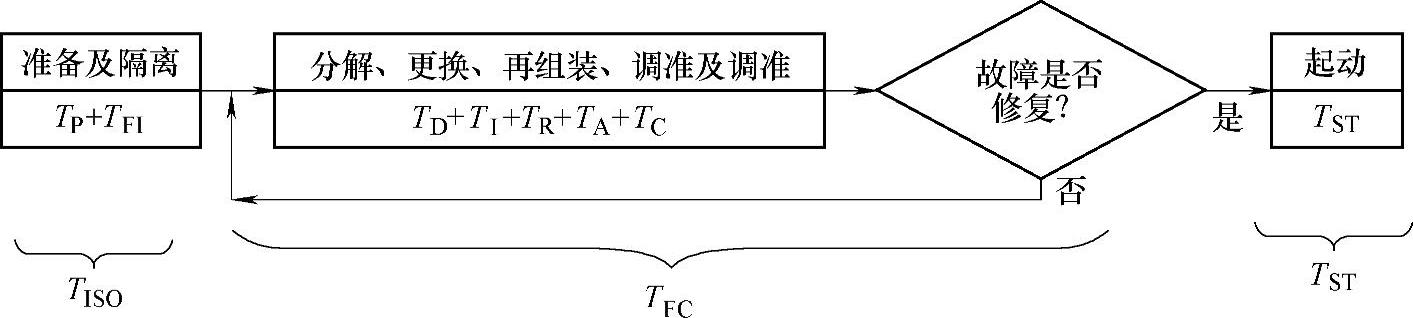
图7-7 重复更换模型