基于时间序列滤波的等维新息灰色预测方法

1.广义数据序列滤波器定义

理论与实践已经证明，灰色预测模型的精度很大程度上取决于原始时间序列的光滑度。原始数据序列的光滑度越高，建立的模型精度就越高；反之，模型的精度就很难达到满意的效果。信号处理中的滤波技术可以大幅度地提高信号的光滑度。对于需要进行灰色预测的原始数据序列来说，可以借鉴信号滤波的方法，即定义一种广义的时间序列滤波器，并通过低通滤波提高数据序列的光滑度，以大幅度提高预测的精度。

借鉴二阶最佳阻尼惯性滤波器，定义一种广义的时间序列二阶低通滤波器，且滤波器不考虑实际时间序列的间隔，只根据滤波器的滤波参数δ来决定滤波后的数据序列的光滑度。δ越小，相当于截止频率越低，滤波后的时间序列越光滑；δ越大，相当于截止频率越高，滤波后的时间序列越接近原始序列。我们称这种数据序列二阶低通滤波器为δ滤波器，它的传递函数如下式所示：

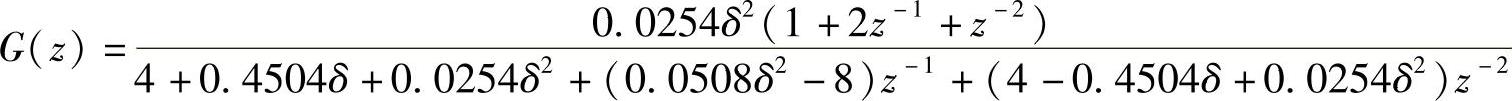
2.灰色等维新息模型(www.xing528.com)

在实际应用中，为了提高灰色模型中长期预测的精度，可以将相继进入系统的扰动因素不断地考虑进去，也就是说可以将GM（1，1）模型每一个新得到的实际数据置入x（0）中，重新建立GM（1，1）模型重新预测，这就是新信息模型。但是，随着时间的推移和新信息的不断植入，一方面系统积累的老信息不断地增多，建模的运算量不断地增大；另一方面老数据的信息随着时间的推移越来越不适应新的情况。为了更能适应灰色系统不断发展变化的实际情况，以及提高灰色GM（1，1）模型的预测精度，研究灰色系统理论的专家和学者们又提出了新的数据处理措施和建模技术，即每补充一个新信息的同时去掉一个最老的信息。这样既考虑了随着时间的推移，老信息功能的不断退化和新信息功能的不断增强，又使系统能适应不断发展变化的实际情况。因此，这种利用补充新数据、去掉老数据进行灰色建模得到的模型称为基于传统GM（1，1）模型的灰色新陈代谢模型。由于灰色新陈代谢模型在建模过程中建模数据的个数，即模型的维数始终保持不变，所以也称为灰色等维新息模型。灰色等维新息模型既克服了传统GM（1，1）模型中数学模型固定不变的弊病，又利用了灰色预测法短期预测精度高的优点，使预测模型得到有效修正、预测精度得到明显提高、灰色预测能满足中长期预测的要求。

3.基于δ滤波器的等维新息灰色预测方法

使用GM（1，1）模型进行灰色预测需要的原始数据序列至少为4个数据，因此灰色预测只能从第4个数据开始。设进行等维新息预测的建模序列维数为N，则当历史数据总量小于等于N时，以所有历史数据经过δ滤波器滤波后作为原始建模序列进行预测；当历史数据量大于N时，采用最新的N个数据经过δ滤波器滤波后作为原始建模序列进行等维新息预测。设时间序列所有值应大于σ，如果出现某点的值不大于σ，说明此点为奇异点，则去除此点，以前一点的值来代替此点的值；设预测结束的阈值为ε，当实际值超过ε时，停止预测，当实际值小于ε时，预测在当前值以后的多少点处，估计值超过ε。基于δ滤波器的等维新息灰色预测方法的流程如图6-25所示^[11]。