基于小波能谱熵的滚动轴承振动特征提取

1.小波能谱熵理论

小波熵理论于1998年提出，Blanco基于小波变换定义了小波熵，并用于ERPs（Event Related Potentials）的分析；其后，不少学者将其用于分析EEG（Electro Encephalogram）等非平稳信号，在EEG信号检测与分类中取得了较好的效果。

小波能谱熵的定义方法：设信号x（n）经小波包变换后，在第j层分解尺度下的分解序列为S_jk，（k=0～2^j-1），D_k（n）为单支重构后得到的信号分量。设E₁，E₂，…，E₂j为信号在j尺度上的熵，则在尺度域E上形成了对信号能量的一种划分。其中，E_k=D_k∣（n）∣²，n为时间序列，n=1，2，…，N，N为所分析信号的采样点数。

由正交小波变换的特性可知，在某一时间窗内信号的总功率E等于各分量功率E_k之和。设p_k=E_k/E，则

于是，定义相应的小波能谱熵W_EE（Wavelet Energy Entropy）为

2.基于小波能谱熵的特征提取方法

根据上面介绍的小波能谱熵理论，可以归纳出基于小波能谱熵的滚动轴承预测特征提取方法的流程如图6-16所示，主要步骤如下：

图6-16 预测特征提取方法的流程

1）信号的预处理。为使不同状态下的信号具有可比性，对滚动轴承的原始振动信号x_i进行规范化预处理：

式中，μ和σ分别为信号的均值和标准差。(www.xing528.com)

经过预处理后信号的统计规律不发生变化，因此不会影响预测的结果。

2）小波包分解。首先，按照前面介绍的理论，对滚动轴承各个特征频率进行计算。初步确定该滚动轴承的频率构成；然后通过对各个特征频率的分析确定小波包分解的层数（假设为3层）。由于Daubechies（db）系列小波的正交、紧支特性，并对不规则信号较为敏感，所以可以拟选用db系列小波对预处理后的信号进行3层小波包分解，对第3层的小波包系数（V₃₁～V₃₈）重构后得到2³个频率段（各个频率段对应的频率范围为（kf_max/2³，（k+1）f_max/2³），其中k为频率段序号，f_max为信号的上限频率）的小波包系数D_k（n），然后通过式E_k=∣D_k（n）∣²求得各频率段小波包系数的能谱。

3）相对小波能谱的计算。为了对这2³个频率段的能谱进行比较。由式p_k=E_k/E（其中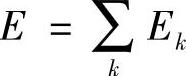，）求出各个频率段的相对小波能谱。

4）小波能谱熵值的计算。最后通过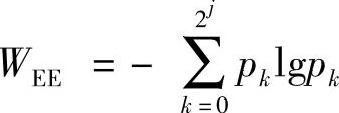求出该段信号的小波能谱熵值W_EE。

3.基于小波能谱熵特征提取的滚动轴承故障预测

前面对小波能谱熵特征提取方法进行了分析，下面对其应用于滚动轴承正常状态和各个等级退化状态的特征提取过程进行研究。

首先，通过对滚动轴承各个特征频率的计算和分析，可以得出，采用db4小波函数对其振动信号进行3层小波包分解，可以有效地提取出振动信号的特征信息；然后根据上面介绍的特征提取方法计算滚动轴承在正常状态及各种退化状态下的小波能谱熵。某型滚动轴承四种状态对应振动信号的30组小波能谱熵如图6-17所示，由下至上分别为正常状态、退化状态1、退化状态2及退化状态3四种状态的小波能谱熵曲线。从图中可以看出，当滚动轴承由正常状态逐渐退化直至出现故障时，小波能谱熵逐渐增大。这是因为滚动轴承处在正常状态时，只在较少的频率段上有能量的分布，能量的分布很不均匀，小波能谱熵值很小。而当滚动轴承故障出现并加剧时，造成多个频率段都有能量的分布，能量分布逐步均匀，小波能谱熵变大。

为描述全寿命过程的故障演化趋势，把小波能谱熵作为一个评判指标，描述整个滚动轴承的全寿命过程。如图6-18所示为某滚动轴承的全寿命周期的小波能谱熵演化趋势。从该图中可以看出，当观测序列数为12时，小波能谱熵值发生了突变，经过检测，该时刻为状态转移点，随着时间的推移，小波能谱熵值逐渐增大，说明该轴承的故障严重程度也逐渐加大，在整个观测序列里，可以根据小波能谱熵的大小把该过程分为四个阶段。因此，小波能谱熵能合理的描述滚动轴承的故障演化趋势，以其作为预测特征值，能有效地提高故障预测的精度。

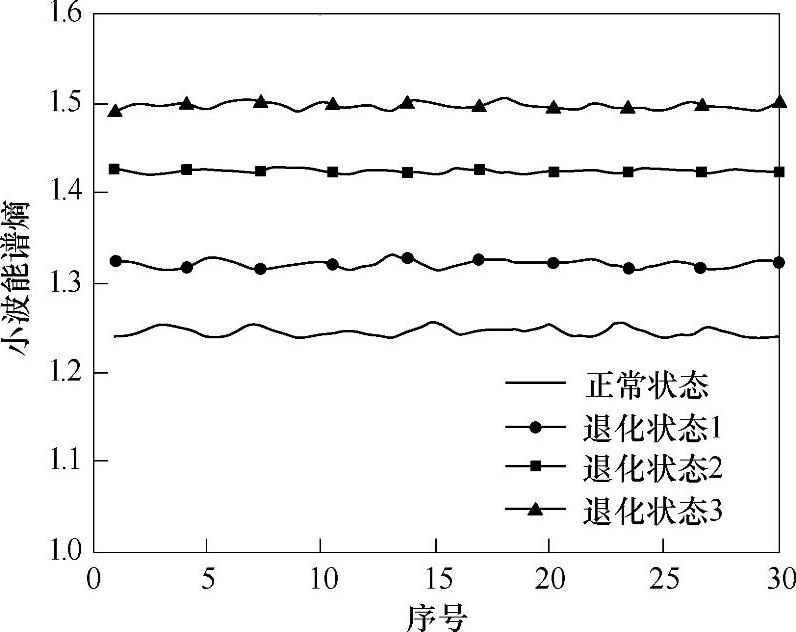
图6-17 某型滚动轴承四种状态对应振动信号的30组小波能谱熵

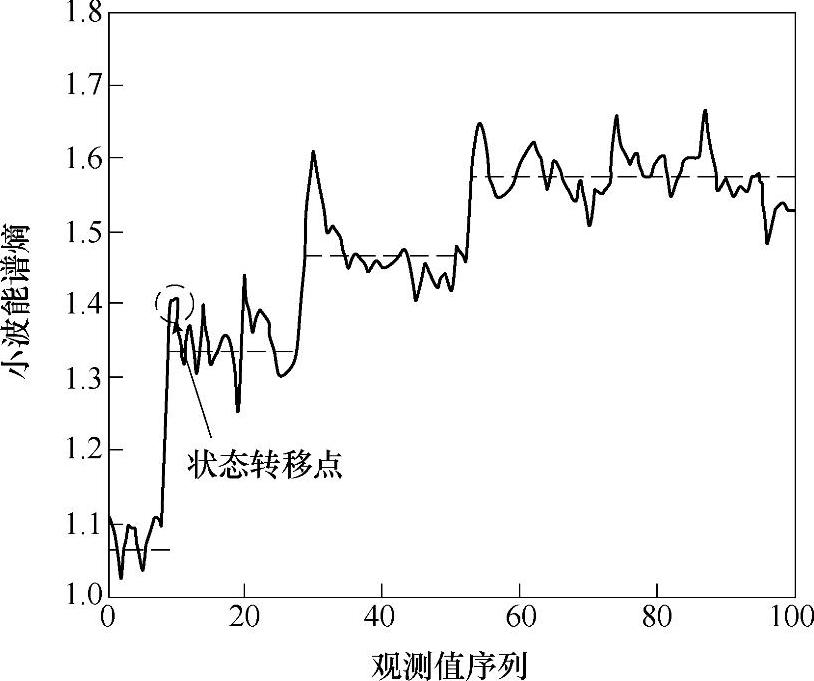
图6-18 某型滚动轴承全寿命周期的小波能谱熵演化趋势