滚动轴承故障演化机理分析

滚动轴承的典型结构如图2-9所示，它由内圈、外圈、滚动体和保持架四部分组成。内圈、外圈分别与轴颈及轴承座装配在一起。在大多数情况下外圈不动，而内圈随轴回转。滚动体是滚动轴承的核心元件，它使相对运动表面间的滑动摩擦变为滚动摩擦。滚动体的形式有球形、圆柱形、锥柱形和鼓形等。滚动体可在内、外圈滚道上进行滚动。

1.滚动轴承的故障类型

滚动轴承在运行过程中出现的故障按其振动信号的特征不同可分为两大类：一类称为磨损类故障；另一类称为表面损伤类故障，包括点蚀、剥落、擦伤等。

（1）磨损类故障 一般来说，在正常使用情况下，滚动轴承工作表面磨损故障经历时间较长，是一种渐变性故障。轴承表面磨损后产生的振动同正常轴承的振动具有相同的性质，即两者的波形都是无规则的，随机性较强。但磨损后振动水平（幅值）明显高于正常轴承。这就是磨损类故障引起的振动信号的基本特点。由于磨损故障引起的振动信号除了振动水平高于正常轴承外没有别的特征差别，所以诊断这类故障就找不到一种很好的信号处理方法。通常做法是监测振动的有效值和峰值，如果明显高于正常轴承，即判定为磨损。由于磨损不会马上引起轴承破坏，其危害程度远小于表面损伤类故障，所以通常人们最为重视的还是下面要讨论的表面损伤类故障。但是当滚动轴承的内圈出现严重磨损时，轴承会出现偏心现象，当轴旋转时，轴心便会绕外圈中心摆动，此时的振动频率为nf_r（n=1，2，…）。

（2）表面损伤类故障 对于表面损伤类故障，当损伤点滚过轴承元件表面时要产生突变的冲击脉冲力，该脉冲力是一宽带信号，所以必然覆盖轴承系统的高频振动频率而引起谐振，从而产生冲击振动。损伤类故障产生的冲击振动成分从性质上可分成两类：

1）低频振动。是由于轴承元件的工作表面损伤点在运行中反复撞击与之相接触的其他元件表面而产生的低频振动成分，有的文献上称之为轴承的“通过振动”。其发生周期是有规律的，可以从转速和轴承的几何尺寸求得。并且，损伤发生在内、外圈或滚动体上时，频率不同。这一轴承“通过振动”发生的频率称为故障特征频率。下面分析滚动轴承表面损伤发生在内圈、外圈、滚动体上时的振动频率成分。

①轴承内圈损伤。当轴承内圈损伤时，若滚动轴承无径向间隙，会产生频率为nf_r（n=1，2，…）的冲击振动。通常滚动轴承都有径向间隙，且为单边载荷，根据点蚀部分与滚动体发生冲击接触的位置不同，振动的振幅大小会发生周期性的变化，即发生振幅调制。若以轴旋转频率f_r进行振幅调制，这时的振动频率为nZf_i±f_r（n=1，2，…）；若以滚动体的公转频率（即保持架旋转频率）f_c进行振幅调制，这时的振动频率为nZf_i±f_c（n=1，2，…）。

②轴承外圈损伤。当轴承外圈损伤时，在滚动体通过时也会产生冲击振动。由于点蚀的位置与载荷方向的相对位置关系是一定的，所以这时不存在振幅调制的情况，振动频率为nZf_o（n=1，2，…）。(www.xing528.com)

③轴承滚动体损伤。当轴承滚动体产生损伤时，缺陷部位通过内圈或外圈滚道表面时会产生冲击振动。在滚动轴承无径向间隙时，会产生频率为2nf_bc（n=1，2，…）的冲击振动。通常滚动轴承都有径向间隙，因此，同内圈存在点蚀的情况一样，根据点蚀部位与内圈或外圈发生冲击接触的位置不同，也会发生振幅调制的情况，不过此时是以滚动体的公转频率f_c进行振幅调制。这时的振动频率为2nf_bc±f_c（n=1，2，…），利用频谱分析诊断轴承故障时，其基本原理就是察看轴承振动信号中有无这些故障特征频率成分。若有，则可根据这些频率成分的大小进一步确定故障发生的部位（内、外圈或滚动体上）。滚动轴承故障特征频率一般在1kHz以下，是滚动轴承故障的重要特征信息之一。

2）高频振动。是由于损伤冲击作用而诱发的轴承系统的高频固有振动成分。这里所说的“高”是相对故障特征频率而言的。轴承系统的高频固有振动很复杂，如轴承内、外圈的径向弯曲固有振动，滚动体的固有振动，甚至测振传感器的固有振动等都可由损伤冲击而产生并反映在轴承的振动信号中。在这些固有振动中，因为通常测轴承振动时，往往把传感器布置在轴承座上测外圈，所以轴承外圈的径向弯曲固有振动是比较有价值的。

2.滚动轴承的故障演化趋势

趋势分析是设备状态识别和故障预测中的一个重要环节，它对设备的特征参数进行连续监测，然后根据所得到的数据来确定设备目前的运行状态，并对设备将来的运行状态作出估计，最后通过一定的预测方法进一步预测设备的剩余寿命。技术人员可根据趋势分析的结果，合理地安排设备的维修，这对于设备维护和维修决策具有重要的意义。因而，振动信号的趋势分析作为设备状态预测的最主要方法一直受到人们的关注。趋势分析的关键是要定义一个量，它能综合反映设备的运行状态，且对出现的异常有较高的敏感性。对大多数旋转机械而言，如水轮机、燃气轮机等，它们的运行过程具有周期性。所以，尽管系统异常状态的种类和形式多种多样，从信号的角度来看，出现异常状态就是在统计特性平稳有序的正常信号中混杂了不一致的异常信号。因而分析的重点在于如何选择一个能反映系统信号统计特征的参数，用该参数来对系统状态进行评估。由于小波变换具有多尺度和局部特性好的优点，结合信息论中熵的理论，人们定义了多尺度下的小波熵，可以来度量信号的统计特性。

对于一个具体的机械部件而言，在失效之前会经历几个退化状态。此处以某型轴承振动信号的小波能谱熵作为评判指标描述这个退化趋势。如图6-15所示描述了某型滚动轴承小波能谱熵的演化趋势，即随着观测值序列增加的变化趋势。随着观测值序列的增加，小波能谱熵逐渐增大并呈现出阶段性的变化。图中把整个观测值序列按照小波能谱熵的大小分成了滚动轴承的正常状态、退化状态1以及退化状态n等几个阶段。

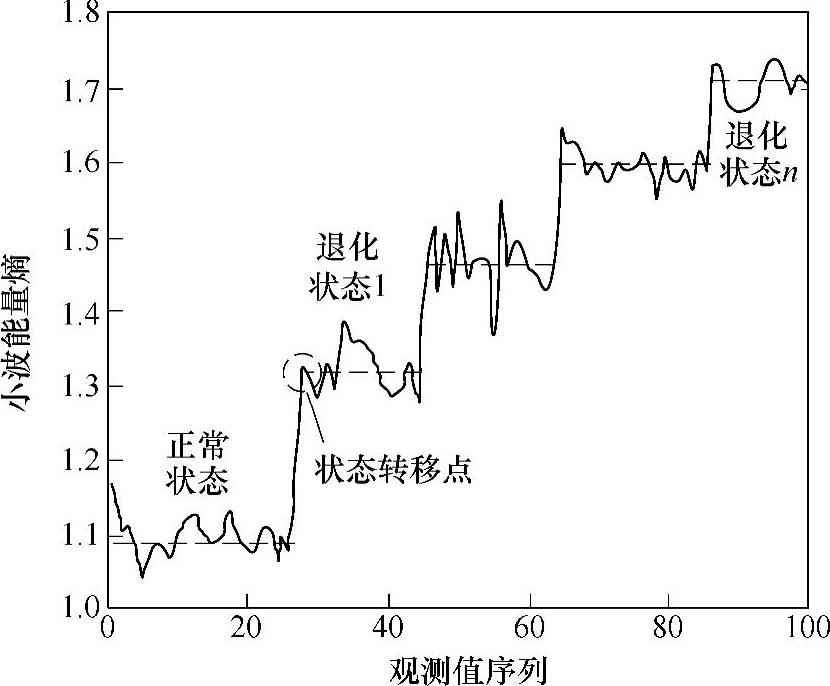
图6-15 某型滚动轴承小波能谱熵的演化趋势