多尺度支持向量机的优化方法

（1）时间序列多尺度分解 工程问题中的时间序列一般是比较复杂的、广义平稳或者非平稳的，是许多因素共同作用的结果，不容易直接分析其变化规律，需将其分解进行逐项分析，再综合最终结果^[6]。一般将时间序列y按不同性质分解为以下四个部分的组合：

y=f（t，c，s，i） （6-5）

式中，t为趋势分量，描述由于某种根本性因素影响，时间序列的中长期变化趋势；c为循环分量，描述趋势曲线在长期时间内呈现摆动的现象；s为季节分量，描述时间序列由于自然条件影响，随季节转变的周期性变动；i为不规则分量，描述随机因素引起的序列变动。

上述四个部分分量若相互独立，则为相加关系；若相互关联，则为相乘关系。以加法模型为例，数据分解的步骤如下所示：①通过移动平均得到趋势循环量（t+c），则季节变动和不规则变动之和为（s+i）=y-（t+c）；②利用曲线拟合等方法求出趋势分量t，则循环分量c=（t+c）-t；③计算各周期中相同期的值的平均数，并进行调整后，作为季节分量s的值，则不规则分量i=（s+i）-s。

（2）相空间重构 在现实系统的研究中，由于某些客观条件的限制，只能观测到系统某个单一指标的时间序列。为了更有效地建立预测模型，需要深入挖掘数据信息，因此，将一维信息转换为矩阵形式，以获得数据间的关联关系，并挖掘到尽可能大的信息量，该方法称为相空间重构。

相空间重构的基本方法是通过一维的时间序列，选择适当的嵌入空间，将原始的一维时间序列转化为多维相空间。以{x_p}为预测目标值，将{x_p-1，x_p-2，…，x_p-k}作为相关量，建立滑动时间窗口x_p={x_p-1，x_p-2，…，x_p-k}和输出之间的关系y_p={x_p}映射关系：R^k→R，k为嵌入维数。经过变换，预测模型的输入矩阵X和输出向量y：

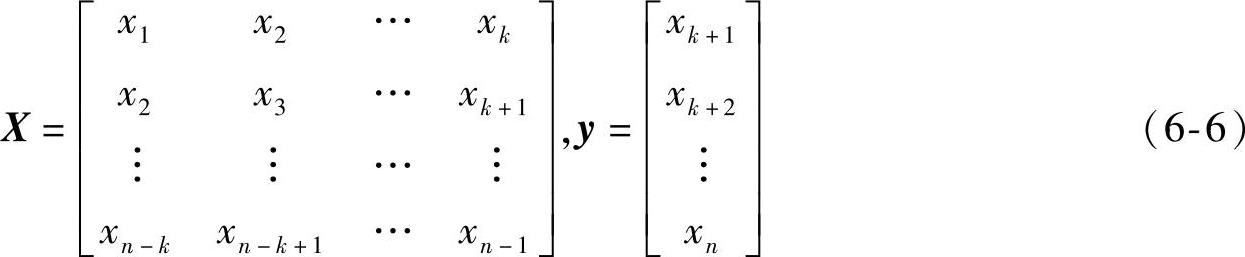
一般来说，嵌入维数的选取以最终预报误差（Final Predictive Error，FPE）最小为准则。FPE准则的基本思想是，用模型一步预报误差的方差来判定回归模型阶数是否适用。如果某个适用的回归模型是由某一序列拟合得来的，则利用该模型对该序列进一步预测，所得的预测误差一定是最小的。一步预报误差的方差越小，就认为模型拟合越好。

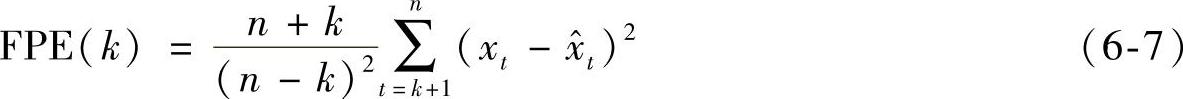
式中，x_t和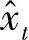分别表示实际值和预测值。

FPE（k）随着k发生变化，因此可以找到一个最优值k_opt，使得FPE（k）最小。该值即为最佳嵌入维数。在得到输入输出样本和最佳嵌入维数之后就可以进行相空间重构。得到最佳嵌入维数k后，可建立映射f∶R^k→R，满足：

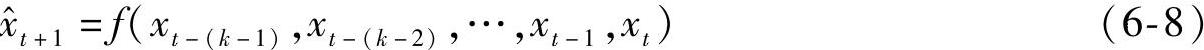
（3）等维信息预测 为提高预测模型中长期预测精度，将相继得到的实验数据不断考虑进去，更新预测模型输入向量。每补充一个新信息的同时去掉一个最老的信息，这样既考虑了随着时间推移，老信息功能不断退化和新信息功能不断增强，又使系统能适应不断发展变化的实际情况。模型维数始终保持不变，因此称为等维信息预测。

等维信息1步预测以实验数据为基础，每次只预测下一数据点。提前1步预测值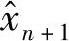为(www.xing528.com)

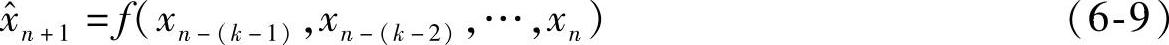
在实际工程应用中，有的维修备件准备需要较长时间，提前1步预测不能及时地将故障征兆反馈给维修人员，因此需要提前多步预测。等维信息多步预测利用已有的实验数据和当前已经预测得到的数据，动态更新输入，保持数据集合维数不变。提前m步的预测值为

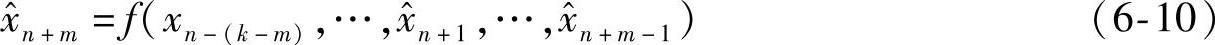
（4）建立多尺度支持向量机 结合支持向量机、多尺度数据分解和相空间重构理论，将时间序列y分解成s个分量：

y=x₁+x₂+…+x_s （6-11）

对于分解得到的x₁，x₂，…，x_s，采用FPE准则寻找最佳嵌入维数k₁，k₂，…，k_s，利用支持向量机建立预测模型，得到预测函数f₁，f₂，…，f_s，则最终预测值p_y为

选用RBF核函数进行非线性映射：

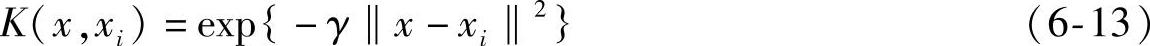
各个分量的预测模型结构如图6-2所示。

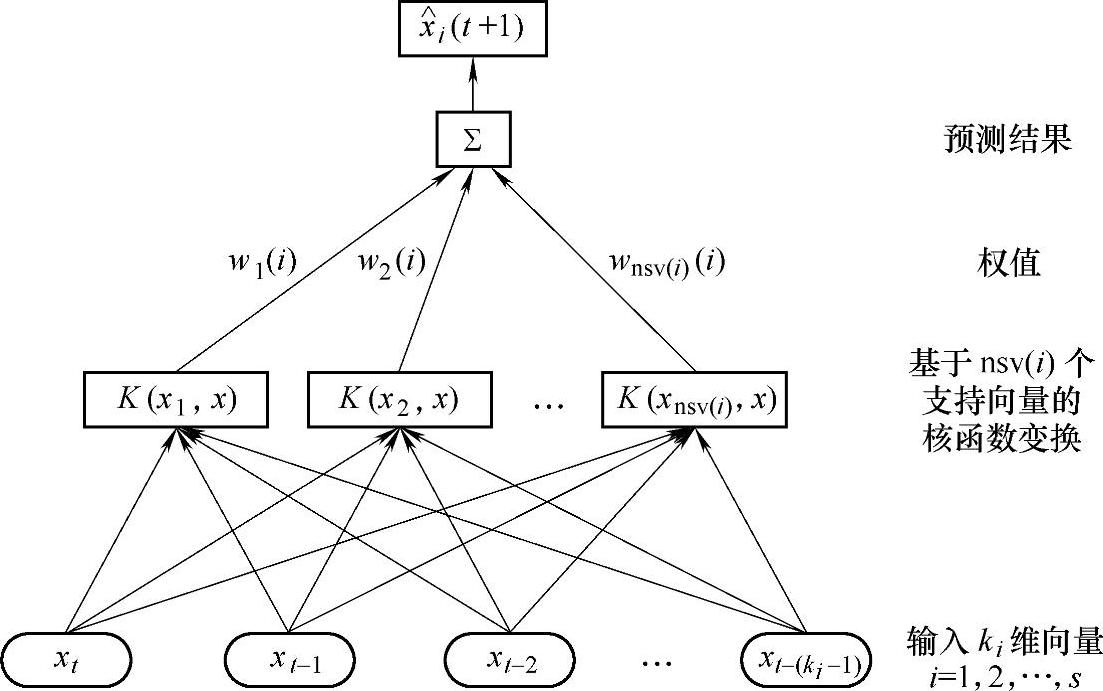
图6-2 各个分量的预测模型结构

上述预测模型中，惩罚系数c控制对超出误差的样本的惩罚程度，核函数的参数γ控制支持向量对输入量变化的敏感程度。c和γ直接影响支持向量机的预测精度。为了寻找最优的c和γ，采用网格寻优，即令c和γ在一定范围内取离散值，取使得最终训练集预测精度最高的c和γ作为最后模型的参数。在得到支持向量机最优参数后，即可以进行预测^[6]。