时频二维自适应阈值实例分析

液压舵机是典型的液压位置伺服系统（图2-14），主要由电液伺服阀、液压缸和反馈位移传感器等组成。为了便于研究，首先建立舵机的数学模型^[13]。

1）舵机伺服阀的力矩马达传递函数：

2）伺服阀负载流量方程：

3）负载流量连续方程：

4）舵机活塞受力平衡方程：

Ap_f=m_pS²Y+B_pSY+F_l （5-15）

式中，S为拉普拉斯算子；K_v为伺服阀力矩马达增益（m/A）；T_v为力矩马达时间常数（s）；Q_f为伺服阀负载流量（m³/s）；K_Q为伺服阀的流量增益（m²/s）；x_v为伺服阀阀芯位移（m）；K_ce为伺服阀的流量压力系数（m⁵/（N·s））；p_f为负载压力（N/m²）；K_fp为伺服阀压差反馈系数（m⁵/（N·s））；T_p为动压反馈微分时间常数（s）；A为作动器活塞有效面积（m²）；V_t为作动器有效容积（m³）；E_y为油液体积弹性模量（N/m²）；K_cp为作动器总泄漏系数（m⁵/（N·s））；m_p为作动器活塞部分质量（kg）；Y为作动器活塞位移（m）；B_p为作动器活塞阻尼系数（N·s/m）；F_l为作动器负载干扰（N）。

液压舵机系统如图5-8所示。图中，i为伺服阀力矩马达线圈电流（A）。

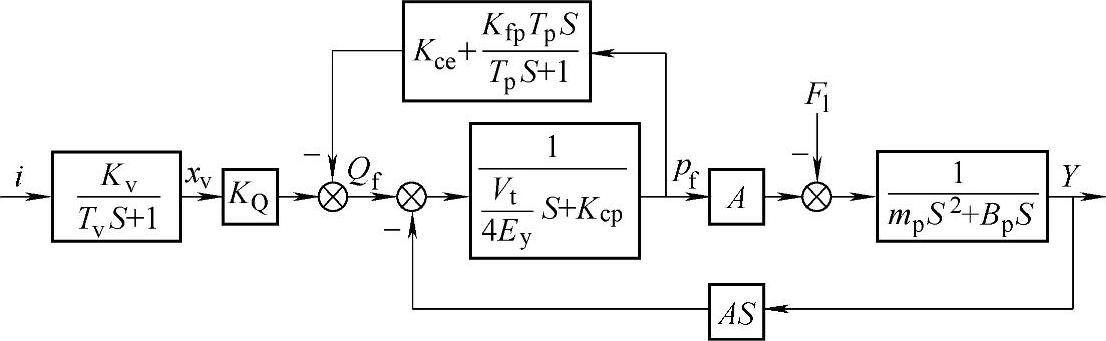
图5-8 液压舵机系统

根据以上关系，同时忽略伺服阀的滞后，得到舵机动力机构的输出为

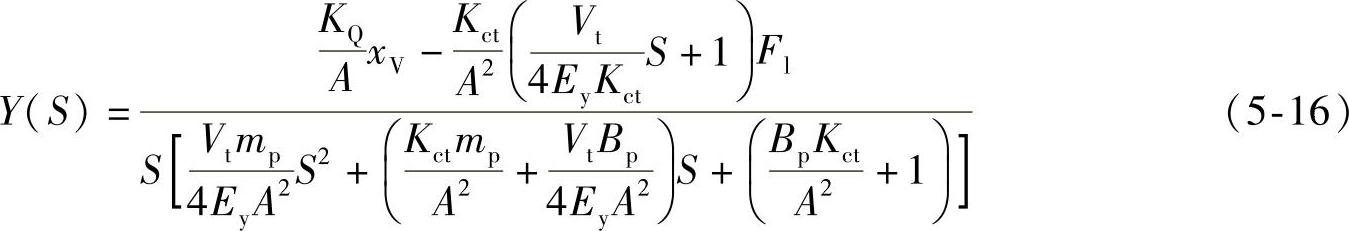
式中，K_ct=K_cp+K_ce为总流量-压力系数。

如果忽略系统阻尼系数，可得简化后的舵机闭环系统如图5-9所示。图中，K_f为反馈系数（rad/A）；K_i为伺服放大器放大系数（A/V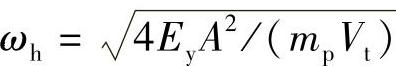）；为液压固有角频率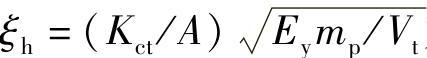，为阻尼比，2ξ_hω_h=4E_yK_ct/V_t。

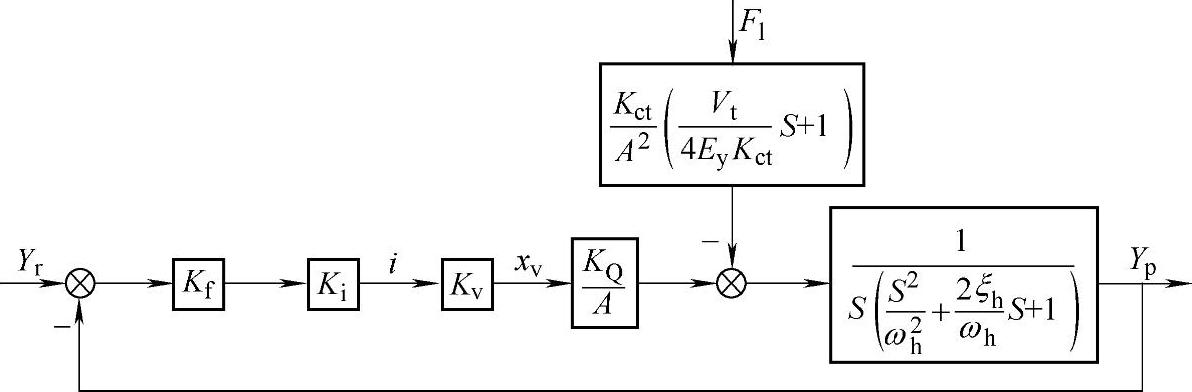
图5-9 简化的舵机系统

由图5-9可得闭环以后的舵机系统对负载干扰的传递函数为(www.xing528.com)

式中，GH=K_fK_iK_vK_Q/A为系统开环增益。

对于电液伺服舵机系统来说，通常ω_b稍大于GH，而为了保证系统的稳定，GH稍小于2ξ_hω_h，所以ω_b与2ξ_hω_h数值接近，而且通常小于ω_nc。所以式（5-17）可以近似地表示为

因此舵机系统的位置刚度近似表示为

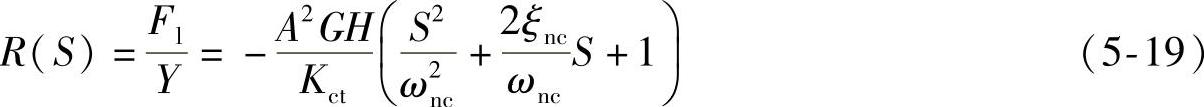
由于一般的电液位置伺服系统都略微欠阻尼，所以舵机最小刚度为

在这一频率下（ω=ω_nc），负载干扰引起的舵机位置输出最大。不同的舵机具有不同的位置刚度，其抗舵面气动力矩干扰的能力各不相同。

采用5.2.3的自适应阈值计算方法，可对液压位置伺服系统正常状态下的响应进行分析，同时也可通过修改PID参数和舵面质量的方法来考察模型的辨识精度及自适应阈值和残差的变化。

（1）舵机正常情况下自适应阈值和残差 如图5-10所示是舵机在正常状态下，舵机各个环节的自适应阈值和残差的关系。从图中可以看出，自适应阈值能够很好地跟随模型的残差变化，图5-10a～d中，残差小于自适应阈值，表明这些模型对应的系统都没有发生故障。

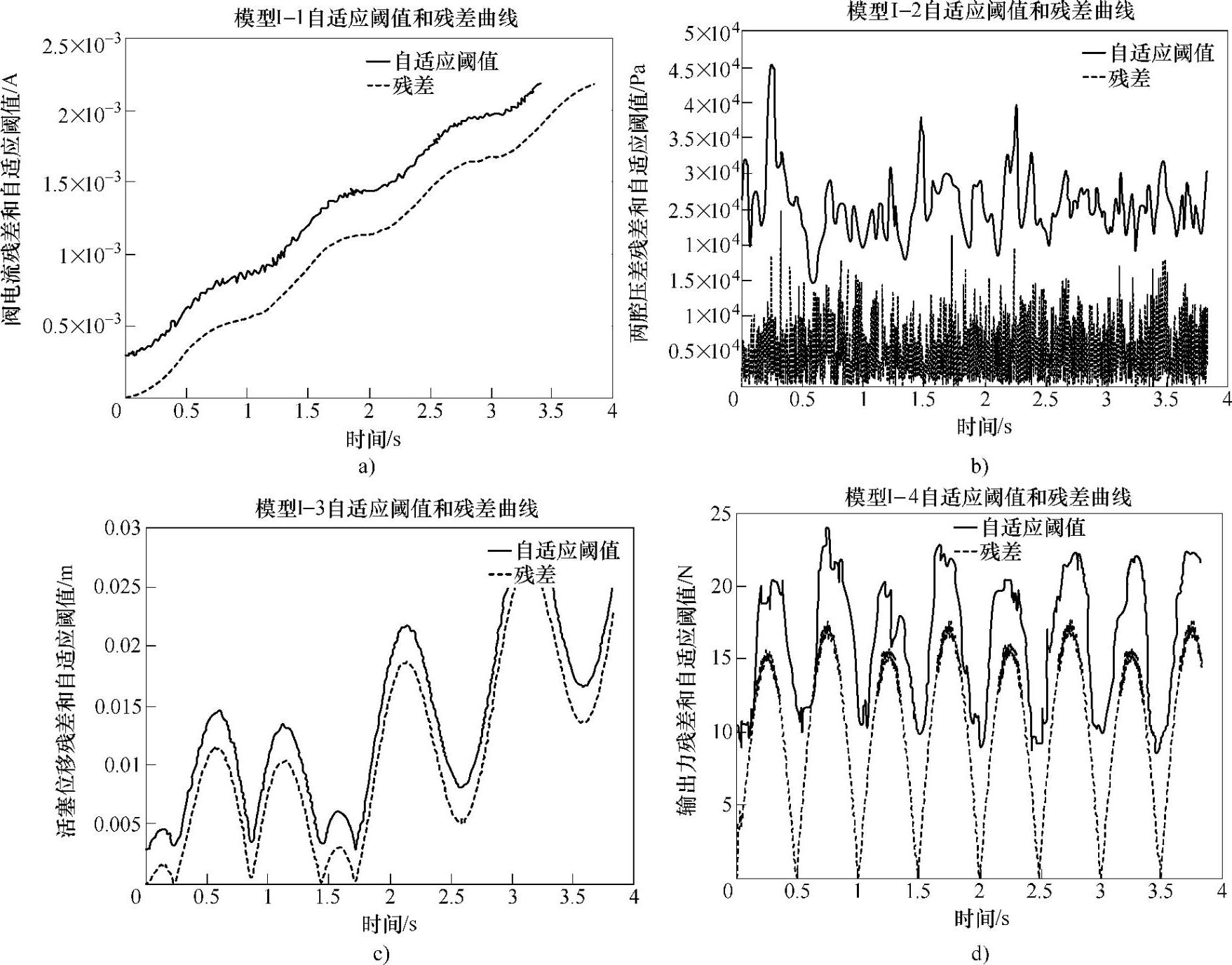
图5-10 舵机正常状态下，自适应阈值和残差的关系

a）舵机正常时放大器自适应阈值和残差曲线（由于残差小于自适应阈值，该子系统诊断为正常） b）舵机正常时伺服阀自适应阈值和残差曲线（由于残差小于自适应阈值，该子系统诊断为正常） c）舵机正常作动器自适应阈值和残差曲线（由于残差小于自适应阈值，该子系统诊断为正常） d）舵机正常舵机自适应阈值和残差曲线（由于残差小于自适应阈值，该子系统诊断为正常）

（2）控制器故障时，自适应阈值和残差及故障诊断结果 如图5-11所示是舵机在控制参数变化状态下，各个模型的自适应阈值和残差的关系图。由于控制器故障会造成控制参数发生变化，该环节输出和模型输出的残差应该超过自适应阈值，如图5-11a所示。而液压伺服阀、作动器和整个液压舵机等环节没有发生故障，因此它们对应的残差小于自适应阈值。

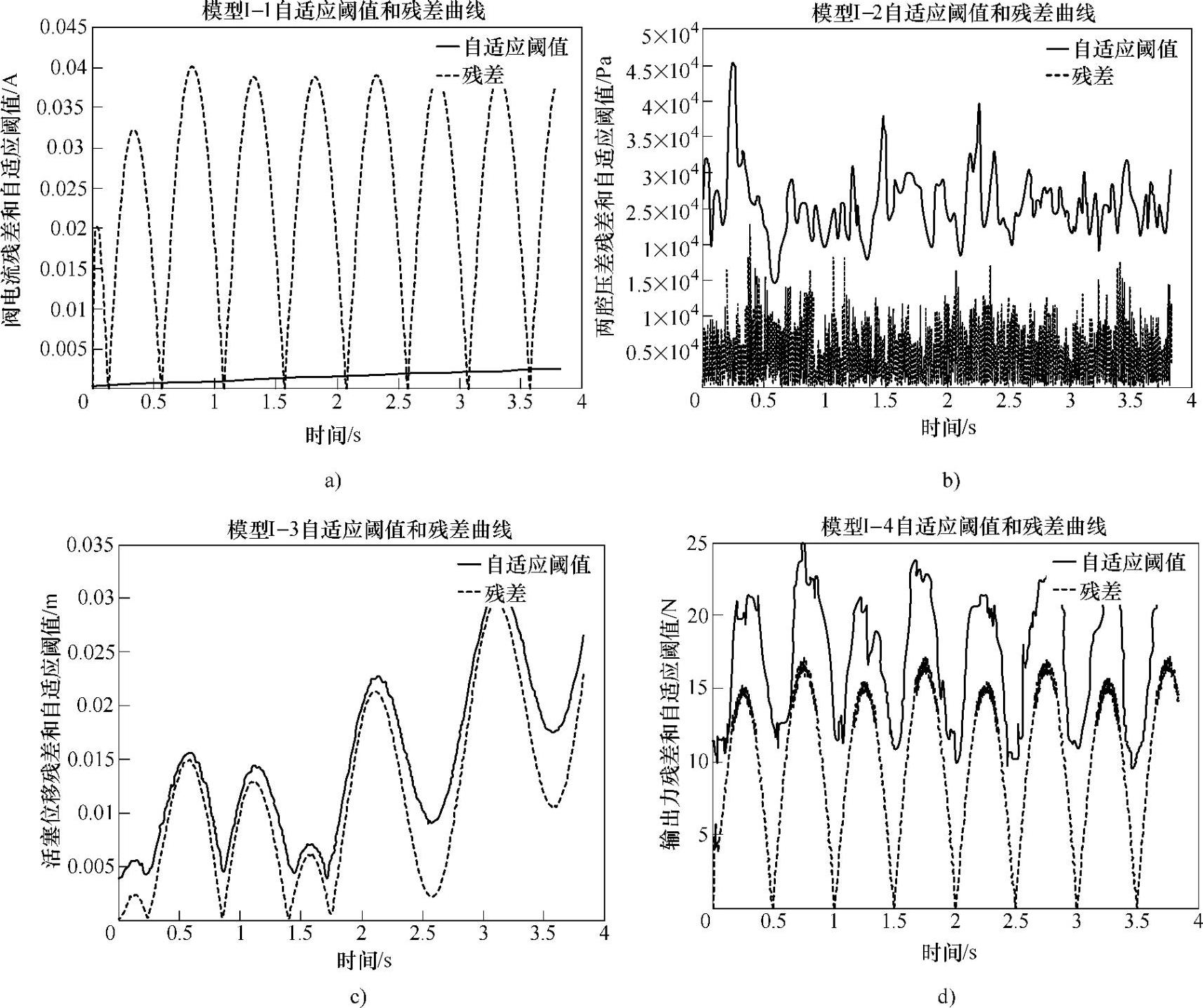
图5-11 控制器故障时，自适应阈值和残差曲线及故障诊断结果

a）控制器故障控制器自适应阈值和残差曲线（残差大于自适应阈值，该子系统诊断为故障） b）控制器故障伺服阀自适应阈值和残差曲线（残差小于自适应阈值，该子系统诊断为正常） c）控制器故障作动器自适应阈值和残差曲线（残差小于自适应阈值，该子系统诊断为正常） d）控制器故障舵机自适应阈值和残差曲线（残差小于自适应阈值，该子系统诊断为正常）