基于模型的液压系统故障诊断方法优化

液压系统中有许多典型的闭环控制系统，如液压位置控制系统、速度控制系统、力控制系统等，这些系统是可以建立起数学模型的，因此建立正常系统的数学模型，实际系统与模型比较来实现故障诊断是可行的方法。基于模型的故障诊断技术的核心思想是估计数学模型，能反映液压系统的正常性能，然后将估计结果与实际物理系统的测量值比较而获得故障信息，如图4-24所示为基于模型的液压伺服系统故障特征提取方法^[11]。从图4-24可以看出，基于模型的故障诊断方法可分为以下两个过程：残差生成器和残差评价，即利用系统数学模型进行行为预测，将预测结果与实际系统测量值比较，获得残差序列；对残差序列进行相关分析，结合历史数据实现故障诊断。

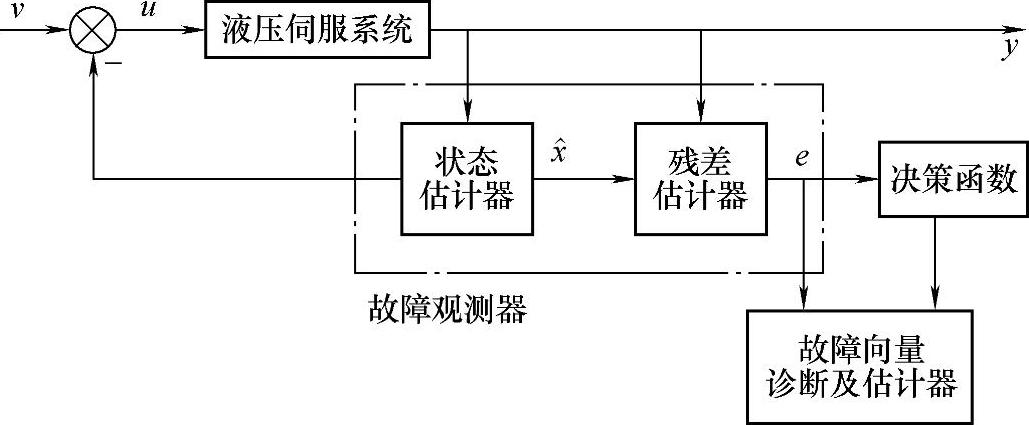
图4-24 基于模型的液压伺服系统故障特征提取方法

设液压伺服系统的动态方程为

式中，x为系统的n×1维状态向量；y为系统的m×1维输出；u为系统的r×1维输入；A为n×n维状态矩阵；B为n×r维输入矩阵；C为m×n维输出矩阵。

式（4-51）称为动态系统的状态方程和观测方程。如果系统完全可观测，那么理论上状态向量x可由输出向量y、输入向量u和这些变量导数的线性组合表示，因而可以构造观测器。

最简单的观测器是建立参数等于原系统参数的模型，这样观测器模型的动态方程可写成：

其中，希望的观测器的状态向量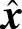与真实系统的状态向量x相同，并利用系统输出与观测器模型输出之间的差值信号经增益阵D反馈到模型输入，如图4-25所示。

故障检测滤波器是一种线性滤波器，它与全状态观测器的设置相同，但设计要求却是不同的。设计全状态观测器时，通过选择增益阵D，使矩阵（A-DC）的特征值具有负实部，这样可以保证设计的观测器是稳定的。设计故障检测滤波器时，不仅要保证滤波器的稳定性，而且要求差值信号能识别系统发生的故障，并具有强的鲁棒性。

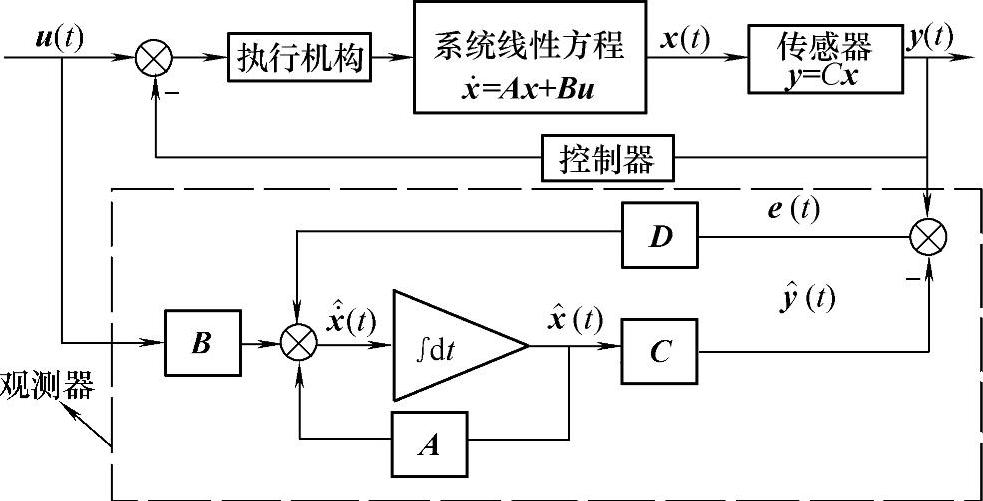
图4-25 故障观测器

若滤波器是稳定的，则正常条件下，滤波器任何初始误差均会逐渐消除，滤波器将跟踪系统的响应，输出误差e（t）将保持为零，除非考虑噪声、干扰或系统建模部分的效应。当系统中某一部件发生故障时，滤波器的模型将不能正确反映发生故障后的系统特性，输出误差将不为零。根据故障检测滤波器的设计限制，输出误差应具有方向性，某个部件的故障对应于一定方向的输入误差。

液压系统中的控制器实现增益反馈控制，及u=-Ky，则式（4-52）变为

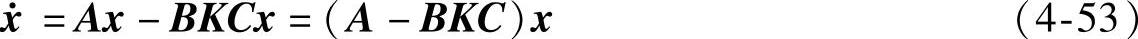
说明增益反馈的效应可包含在A内，而将式（4-53）中的控制输入u看做是独立输入。这样故障检测滤波器方程为

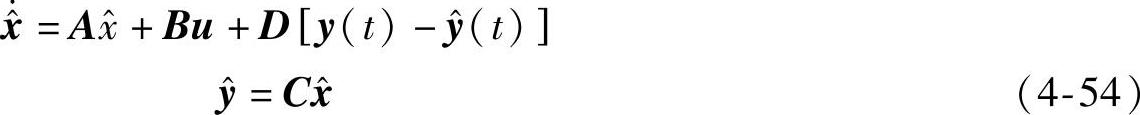
定义：

状态误差

测量误差

则状态误差方程为

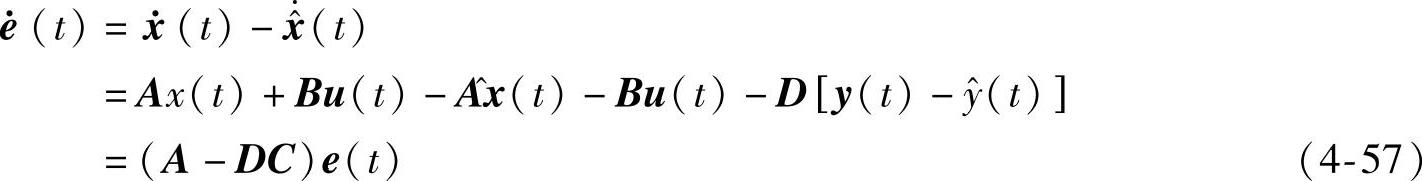
输出误差方程为(www.xing528.com)

根据状态方程误差和输出误差方程可以实现液压伺服系统故障诊断。

由于液压伺服系统在伺服阀、执行机构、管路和负载等部位具有强烈的非线性时变环节，数学模型极其复杂，现有的模型都是在各种假设和近似下得到的线性模型，因此基于数学模型的状态观测误差较大。针对复杂液压系统数学建模困难、基于数学模型故障诊断鲁棒性差的问题，常采用RBF神经网络观测器对液压伺服系统进行状态观测，通过实际系统输出与观测器输出间的误差实现伺服系统的故障诊断，RBF神经网络观测器结构原理如图4-26所示^[16]。

选择RBF神经网络观测器的结构如4-26所示，RBF的第一层为输入层：网络的输入为系统控制指令r和系统的输出的角度信号θ_f；第二层为隐含层，具有6个节点；第三层为输出层：网络的输出为待估计的系统的输出角度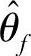。网络参数的确定包括确定网络隐层径向基函数的中心C_j，半径σ和隐层到输出层的权值w。

在RBF网络训练时采用的输入信号是系统的输入指令r和系统的输出θ_f作为网络的输入样本，系统的输出角度θ_f信号作为期望输出的样本。采集大量样本训练RBF网络以确定网络的结构参数，注意：训练网络的样本应涵盖尽量多的数据信息。

当RBF神经网络的结构参数被确定下来后，网络隐层径向基函数的中心C_j，半径σ就被确定下来且保持不变。在正常情况下，网络的输出同系统的输出差值不大，一般在零附近有波动，这是由于系统的干扰等因素造成的。当液压系统出现故障，实际系统输出与RBF网络输出的残差变大，考核该残差形式即可实现液压伺服系统的故障诊断。

如图4-27所示为RBF神经网络对正常系统的逼近曲线，为了提高逼近精度，一般选择尽量多的训练样本。试验中给定的指令信号为频率1Hz，振幅为2的正弦输入量。图4-27中包含了系统的实际输出和RBF神经网络的估计输出，由于两者的差值较小，图中的显示区分度不是很好。如图4-28所示为RBF网络对正常系统的输出跟踪情况误差试验曲线。图4-28中，曲线中的幅值为0.02，误差的精度为1%。这说明网络对正常系统能够达到较高精度的跟踪。

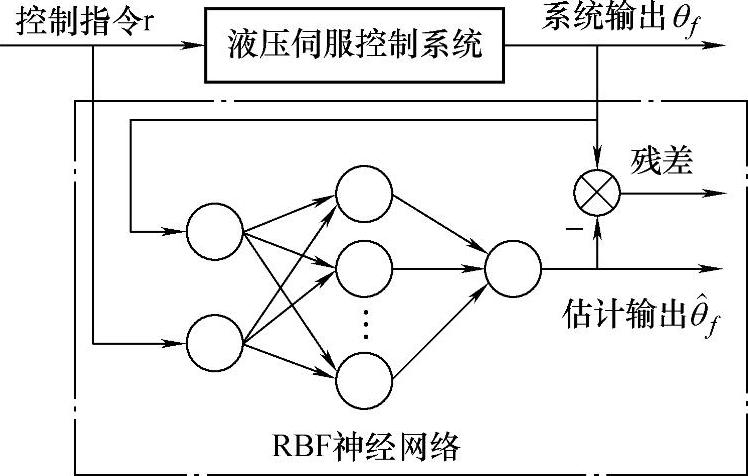
图4-26 RBF神经网络观测器结构

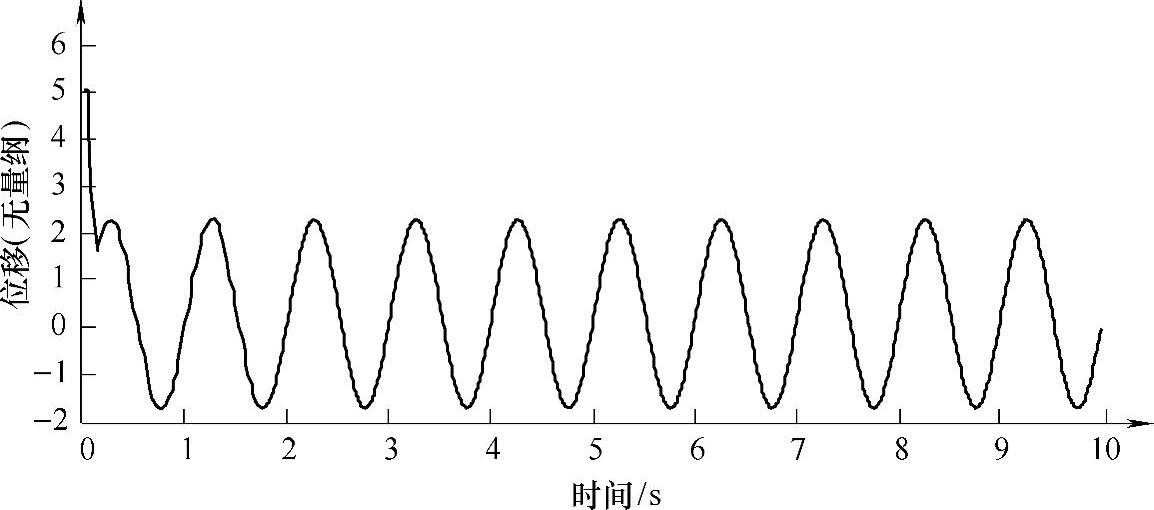
图4-27 RBF神经网络对正常系统的逼近效果

下面基于RBF神经网络进行液压伺服系统故障诊断。

（1）电子放大器故障 电子放大器故障的设置通过改变电子放大器的系数来实现。正常时k_i=4×10^-3，故障时k′_i=8×10^-3，放大系数增大了两倍。图4-29是系统的位移输出残差曲线。

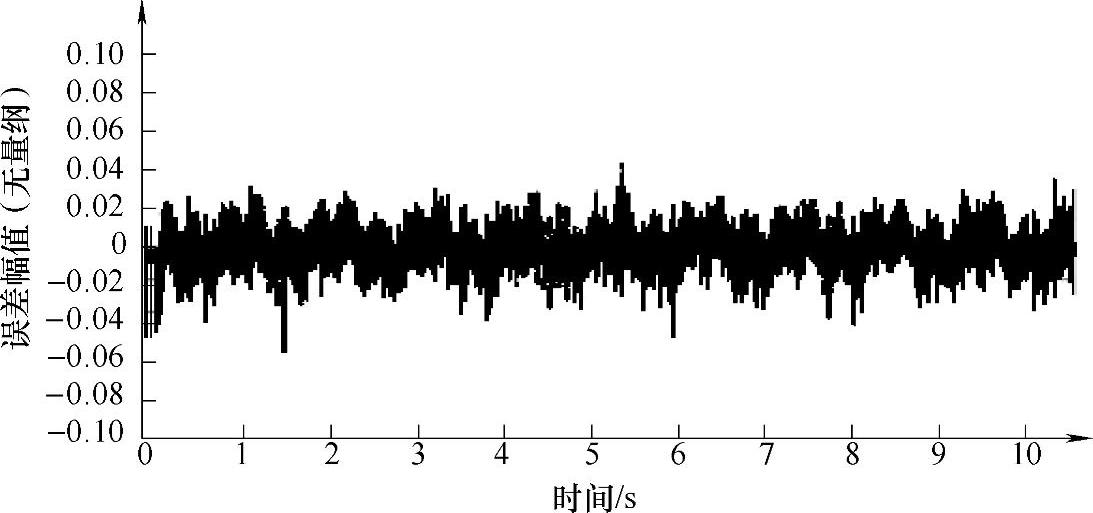
图4-28 RBF网络对正常系统的输出跟踪情况误差试验曲线

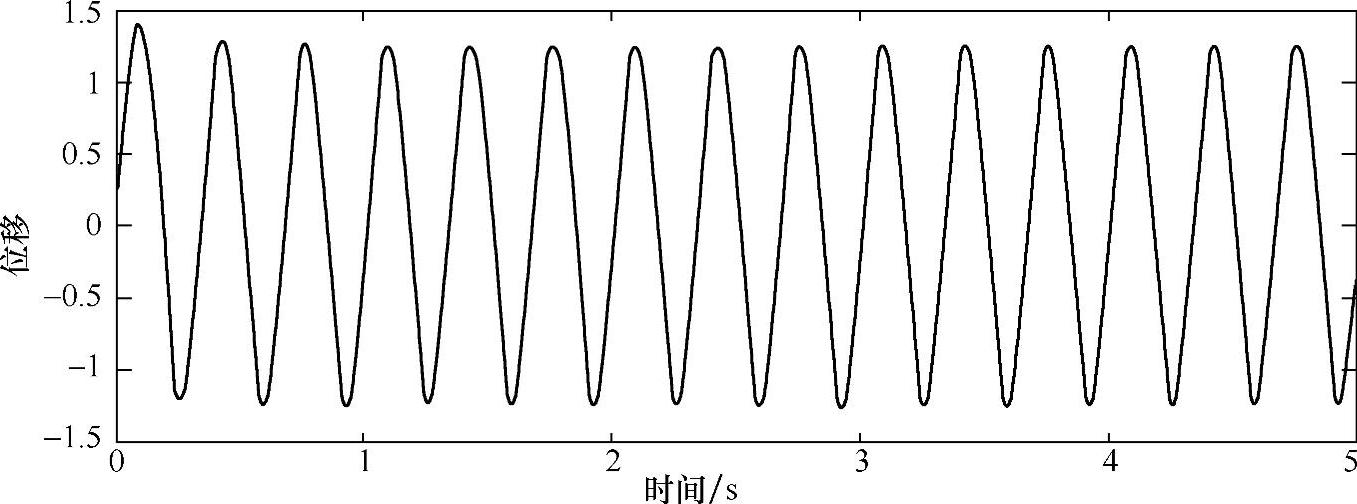
图4-29 电子放大器故障的残差曲线

由图4-29可见，当电子放大器发生故障时，系统的输出位移和网络的估计输出的位移残差不为零，残差幅值较大，残差比正常系统时的残差大8个数量级，通过检测残差曲线可以检测系统是否正常工作。

（2）泄漏故障 泄漏故障是伺服系统常见的故障之一，伺服阀滑阀磨损和液压缸的间隙都会使液压系统出现泄漏增大。为了简化系统设置，不考虑其他影响因素，仅认为泄漏故障体现为数学模型中总的流量压力系数K_ce增大。正常情况下系统的流量压力系数为K_ce=2.0373×10^-11，这里设置其变化量为ΔK_ce=2.0373×10^-11，通过仿真得到系统输出与RBF网络估计的残差曲线，如图4-30所示。

从图4-30可以看出，泄漏故障发生时系统的位移输出达不到指令的要求，则网络的输出和实际系统的输出残差曲线不为零，残差比正常系统时的残差大8个数量级，通过检测残差曲线可以检测系统是否出现故障。

由以上结果可以看出，RBF神经网络对系统辨识的精度很高，系统正常时网络的估计输出和实际输出残差接近于零。但是在系统出现故障时，网络的估计输出和实际的输出残差不再为零，通过检测残差曲线可以进行液压伺服系统的故障诊断。从图4-29和图4-30可以看出，虽然RBF故障观测器可以通过残差判定系统是否出现故障，但是不能实现故障定位。

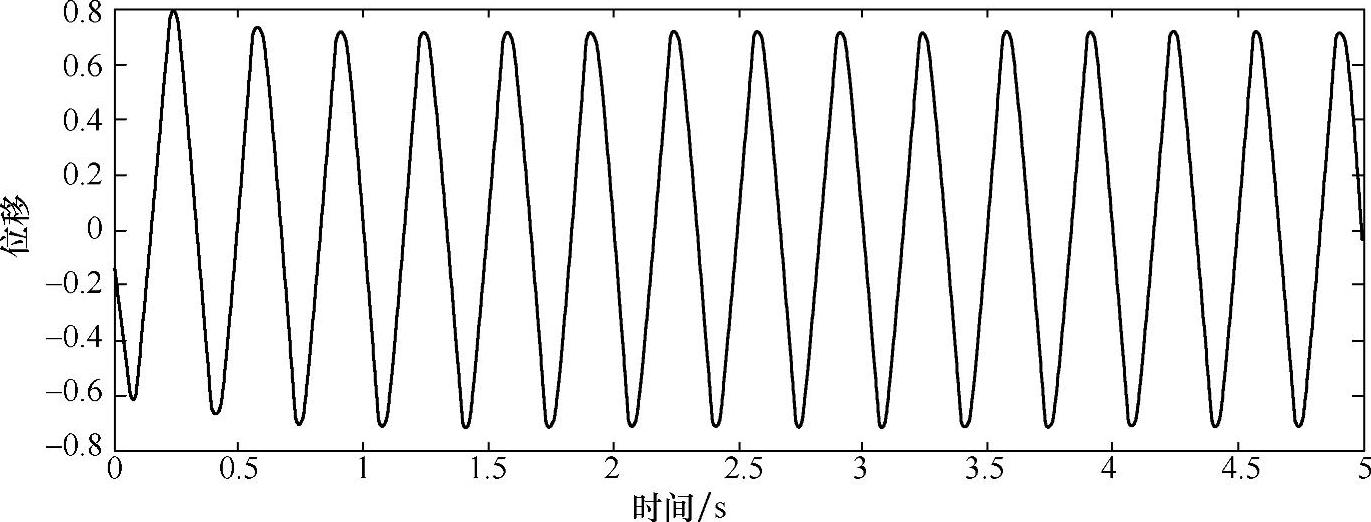
图4-30 泄漏故障的残差曲线