基于神经网络的优化方法

基于信号处理的方法是液压系统故障诊断的有效方法之一，谱图能清晰反应故障与特征信号之间的关系，但该方法往往依赖于频谱的明显特征凸显。而事实上，由于信号谱图常常无法明显表征正常和故障状态，且由于时域信号变化情况下故障阈值对应也动态变化，很难用固定阈值判断出故障特征，实现在线故障诊断。因此利用信号处理提取故障特征后，通常采用神经网络作为故障分类器，即故障信号处理后的故障模式分析，实现从故障征兆到故障原因的非线性映射，基于神经网络模式识别功能的液压系统故障诊断系统原理如图4-19所示。

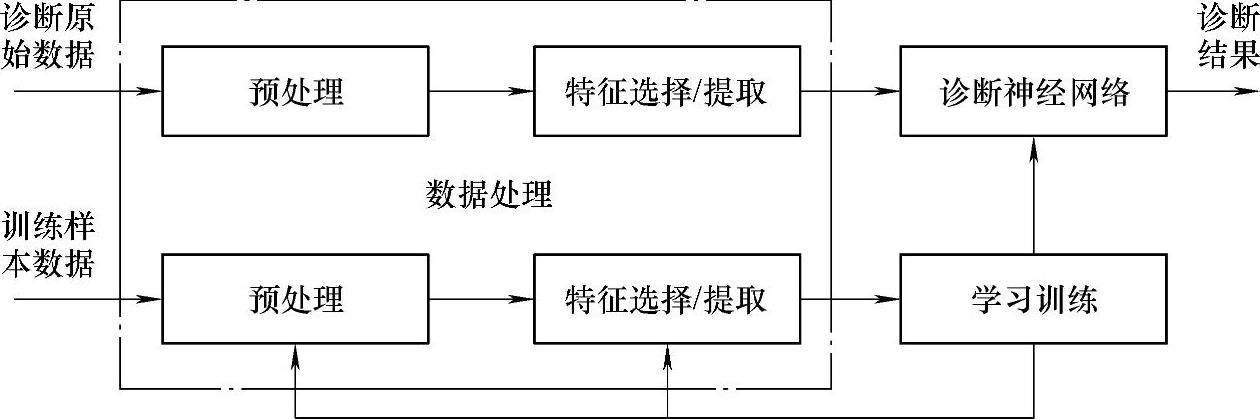
图4-19 基于神经网络模式识别功能的液压系统故障诊断系统原理

下面以BP神经网络为例说明如何基于神经网络进行故障诊断。如图4-20所示是BP神经网络的结构图，该网络由三层即输入层，隐层和输出层组成。输入层的功能函数是一个非线性函数，输出层的功能函数是一个线性函数，w_ij为隐层第j个神经元与输入层第i个神经元之间的连接权值，v_kj为输出层第k个神经元与隐层第j个神经元之间的连接权值。

BP算法的学习过程由正向传播过程和反向传播过程两部分组成，在正向传播过程中，输入模式从输入层经过隐层神经元的处理后，传向输出层，而每一层神经元的状态只影响下一层神经元状态。如果在输出层得不到期望的输出时，则反向传播，此时误差信号从输出层传播并沿途调整各层间连接权值和阈值，且使误差不断减小，直到满足精度要求。该算法实际上是求误差函数的极小值，它通过多个样本的反复训练，并采用最快下降法使得权值沿着误差函数负梯度方向改变，直至收敛到最小点。

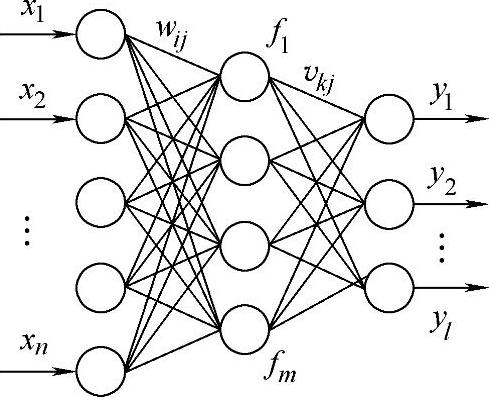
图4-20 BP神经网络的结构

BP算法的推导过程如下：

（1）正向传播过程

输入层：单元i的输出值o_i等于其输入值x_i。

隐层：对于第j个隐单元，其输入值net_j为其前一层各单元的输出值o_i的加权和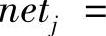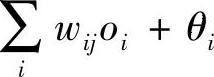；输出值为a_j=f（net_j），f为sigmoid函数，即

输出层：因为输出层单元的作用函数为线性，所以输出值为输入值的加权和，对于第k个输出单元，输出值y_k为

（2）反向传播过程 首先定义误差函数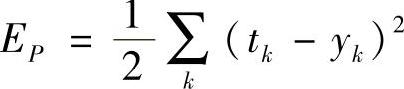，BP学习算法采用梯度下降法调整权值，每次调整的量为(www.xing528.com)

式中，0＜η＜1，成为学习率。由此式可以得到权值得修正量公式。

对于输出层与隐层之间的权值υ；

Δυ_kj=ηδ_ka_j （4-9）

式中，δ_k=y_k（1-y_k）（t_k-y_k）。

对于隐层与输入层之间的权值w：

Δw_ji=ηδ_jo_i （4-10）

式中，。

一般情况下，BP神经网络的输入向量的物理含义各不相同，在数量级上相差很大，譬如特征频率点处的幅值和能量值相差就可达到几个数量级，如将这些量直接输入到神经网络进行分类，必然导致数量级小的输入量对分类影响小，即数量级小的量容易被忽略。为了减小这种影响，一般情况下BP神经网络的输入向量都要进行归一化处理。

神经网络故障诊断的步骤如下：

1）产生数据样本集。包括原始数据的收集、数据分析、变量选择及数据的预处理，只有经过这些必要的步骤后，才能对神经网络进行有效的学习和训练。首先要在大量的原始测量数据中确定最主要的输入模式，即找出大量数据中体现数据本质特征的量。在确定了输入量后，需要进行尺度变换和预处理，即剔除会引起神经网络不稳定的数据奇异点；检验数据中可能存在的周期性、固定变化趋势等；并将数据归一化，即变换到[-1，1]或[0，1]的范围。对数据的预先处理有利于神经网络的学习和训练。

2）确定网络的类型结构。首先根据问题的性质和任务的要求来选择合适的网络类型。一般从已有的网络类型中选用一种相对简单又能满足要求的网络。然后选择网络的结构和参数。即选择网络的层数、每层的节点数、初始权值、阈值、学习算法、数值修改频度、节点变换函数、学习率等。尽管有些项的选择有一些指导原则，但更多的是靠经验和试验。

3）网络的训练和测试。最后一步是对网络的训练和测试，即对样本数据反复使用以训练网络，反复的训练直至网络对于输入输出获得合适的映射结果。在神经网络训练好之后，神经网络就可以对液压系统的正常状态和各种故障状态具有区分度，当实际样本输入到神经网络后神经网络就可以自动判断液压系统是正常的还是有故障。