压力特征信号的处理方法探析

了解了以上压力脉动产生的原因后，在液压系统中检测到的压力信号需要对以上压力脉动进行滤除，才能有效得到故障特征。为了提高压力信号特征提取的有效性，常采用以下信号处理方法消除干扰和提高故障特征的识别度。

（1）基于平稳小波分解和重构的压力信号脉动项与波动项的分离 鉴于小波分解可以对信号全貌及其局部特性进行双重分析，采用3.1.4中介绍的小波包分解和重构技术将压力信号分解到不同的频率通道中，就可以在一定频率范围内将信号的冲击成分和平稳成分区分开来^[21]。如图3-13所示为齿轮泵压力信号，调定压力为5MPa时正常出口压力信号如图3-13a所示，齿轮磨损状态出口压力信号如图3-1b所示。

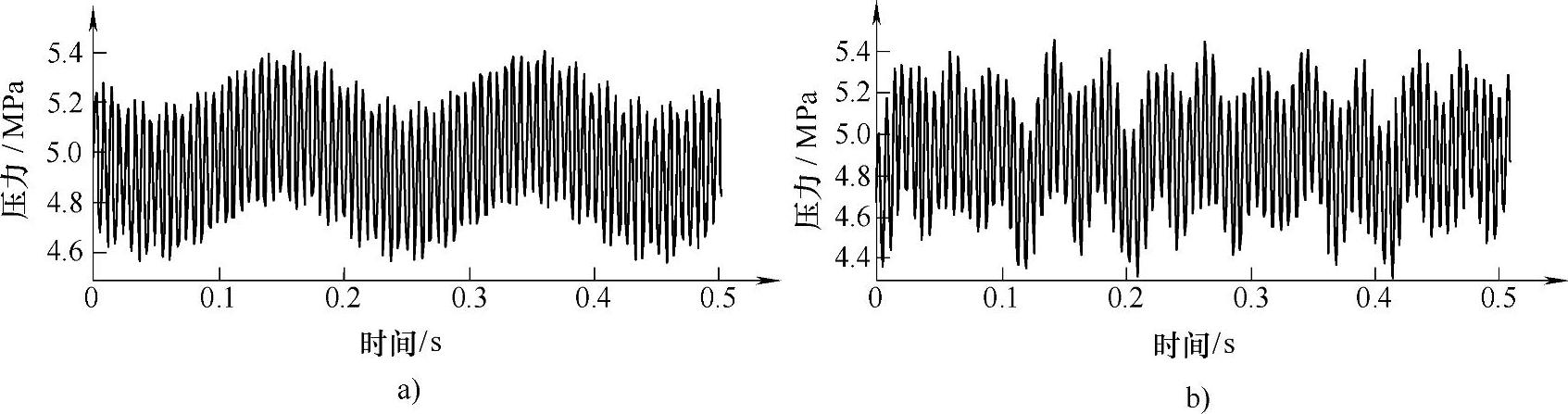
图3-13 齿轮泵压力信号

a）正常状态 b）齿轮磨损

很显然，齿轮泵的输出压力不是稳定的，包含高频压力脉动和低频波动成分。将图3-13b的信号采用db3小波进行6层平稳小波分解，齿轮磨损状态下压力信号的6层平稳小波分解后的结果如图3-14所示。

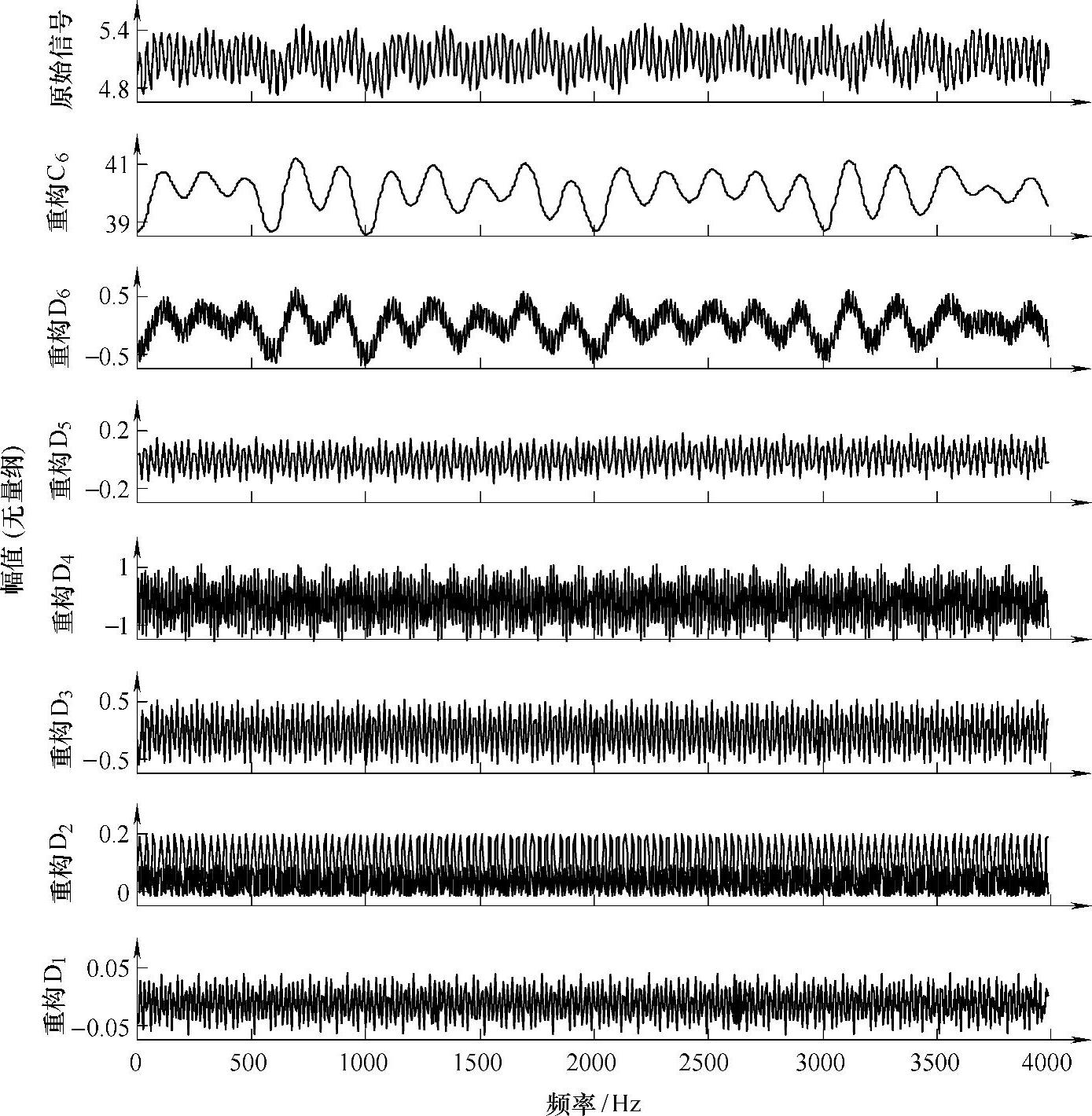
图3-14 齿轮磨损状态下压力信号的6层平稳小波分解后的结果

由图3-14可见，小波分解的部分包含了压力信号的低频波动成分，D_i（i=1～6）对应信号的细节部分，各细节对应的频带为[2500/2ⁱ，2500/2^i-1]，覆盖的频段为39.0625～2500Hz。将细节系数D₁～D₆全部置0，然后将小波分解系数重构可得到压力信号的低频波动部分，从原始信号中减去低频波动部分即可得到高频脉动部分，齿轮磨损状态压力信号的分离结果如图3-15所示。

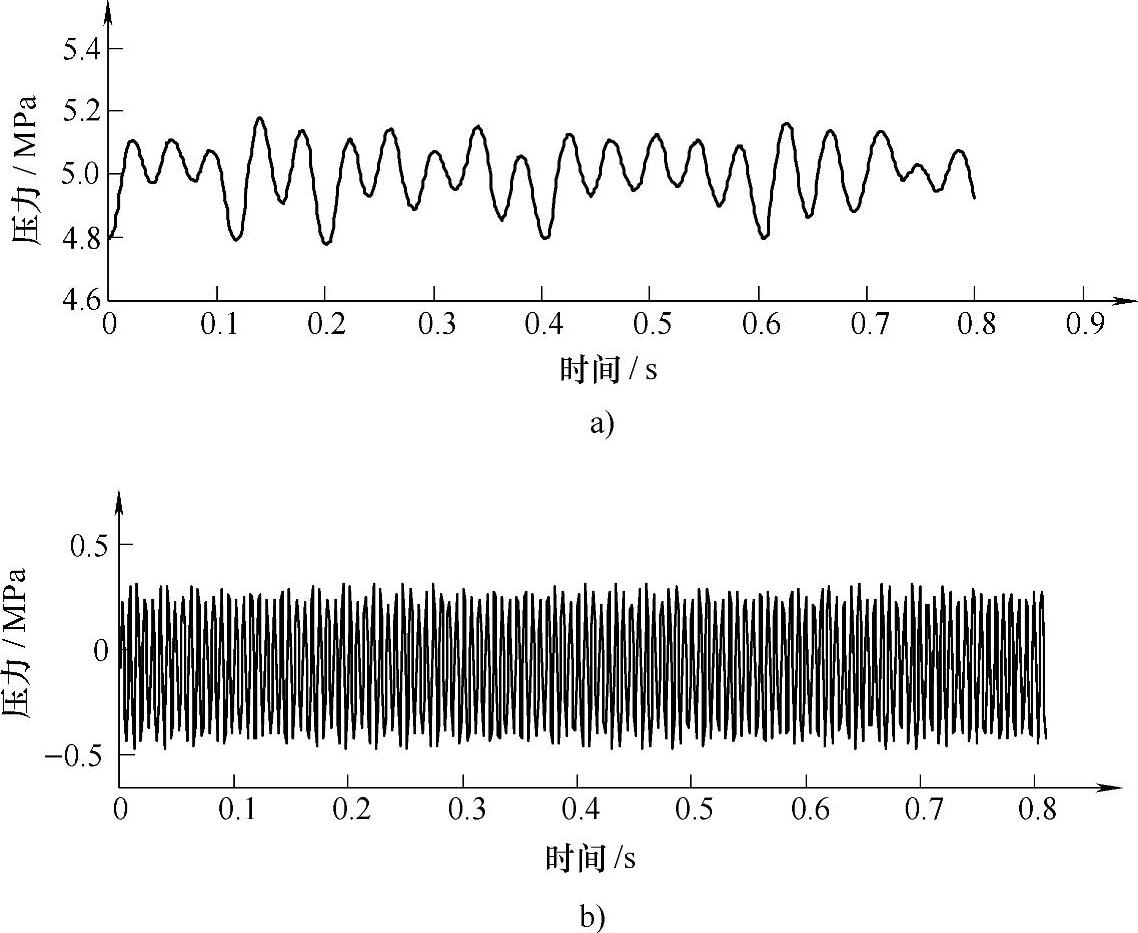
图3-15 齿轮磨损状态压力信号的分离结果

a）低频波动 b）高频脉动

（2）压力信号低频波动项分析与特征提取 压力信号的低频波动项表征压力信号的稳态部分，在同一调定压力下，理论上是平稳的。但由于齿轮泵压力的高频脉动、调压阀的频繁开闭等原因常会引起管路系统的自激振荡，造成压力波动。如图3-16所示为齿轮泵正常和磨损故障下的压力信号。

由图3-16可以看出，当齿轮泵出现磨损故障时压力信号有剧烈的波动，正常状态的波动频率为6.1Hz，该频率与管路结构、调压阀结构和性能有关，是压力信号的高频脉动激起的管路低频共振频率。而齿轮泵故障状态下，压力波动的频率为24.7Hz，与齿轮泵的工频一致，这主要是由于故障齿轮啮合时产生的周期性流量泄漏会激起管路系统同周期的共振和压力脉动。从上面分析可知，压力信号的波动加剧预示着齿轮泵故障的发生。由于波动的幅度与具体的管路系统有关，不同状态在同一管路下才可以比较，而不同管路系统之间不具有可比性。

（3）压力信号高频脉动项分析与特征提取 由齿轮泵的压力脉动机理知，压力信号的高频脉动由流量脉动引起的，与齿轮泵自身的故障状态、泄漏情况更有关系。压力脉动的主要成分与齿轮泵的啮合频率f_m（246.7Hz）一致，其波形与如图3-17所示理想状态下流量脉动的波形大体相似。对图3-15中信号平稳小波变换细节D₁（1250～2500Hz）、D₂（625～1250Hz）和D₃（312.5～625Hz）对应的脉动信号的高频部分，将不同状态下压力信号D₁、D₂、D₃项提取出来进行重构，压力脉动特征频带重构结果及其功率谱如图3-17所示。

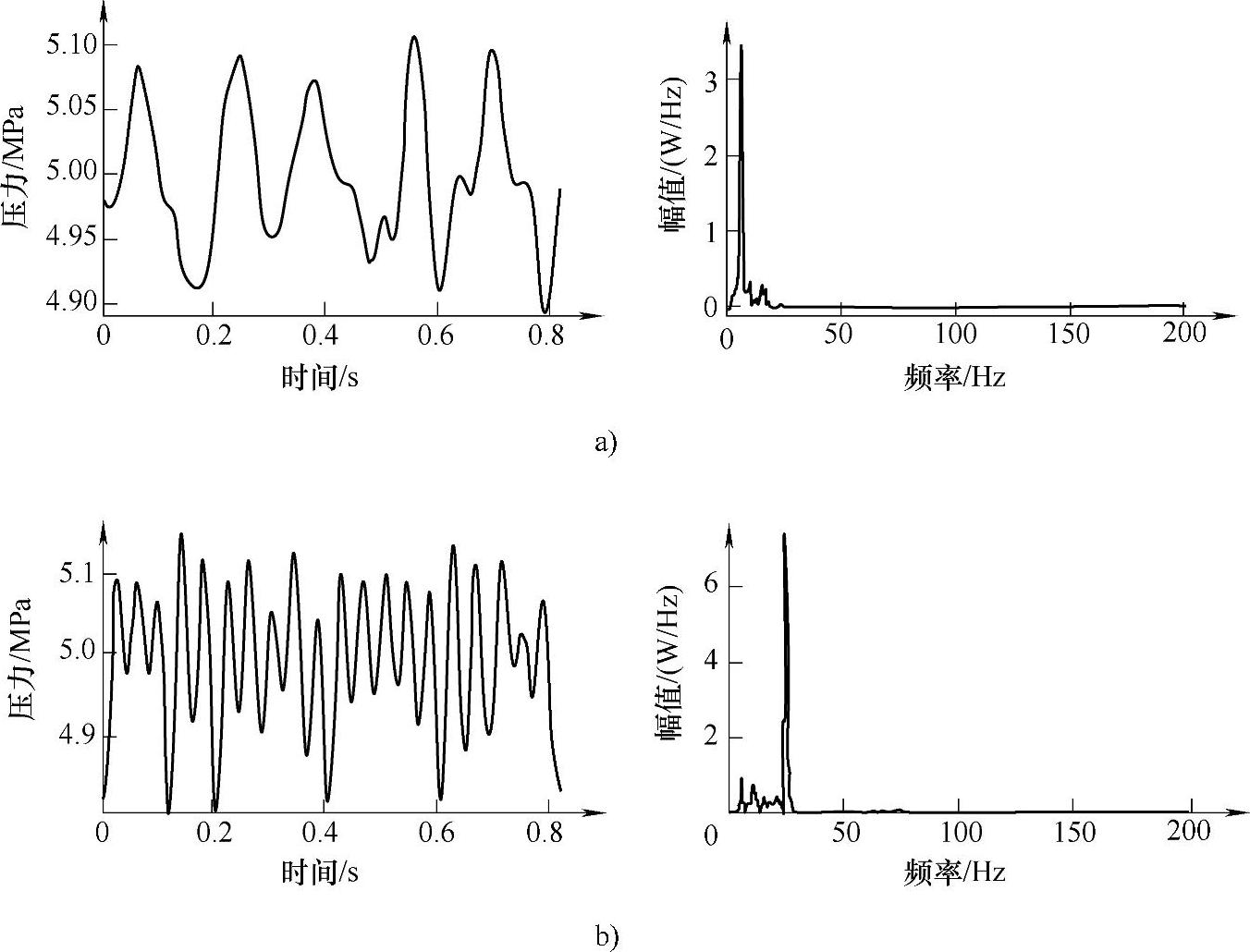
图3-16 齿轮泵正常和磨损故障下的压力信号

a）正常状态 b）齿轮磨损

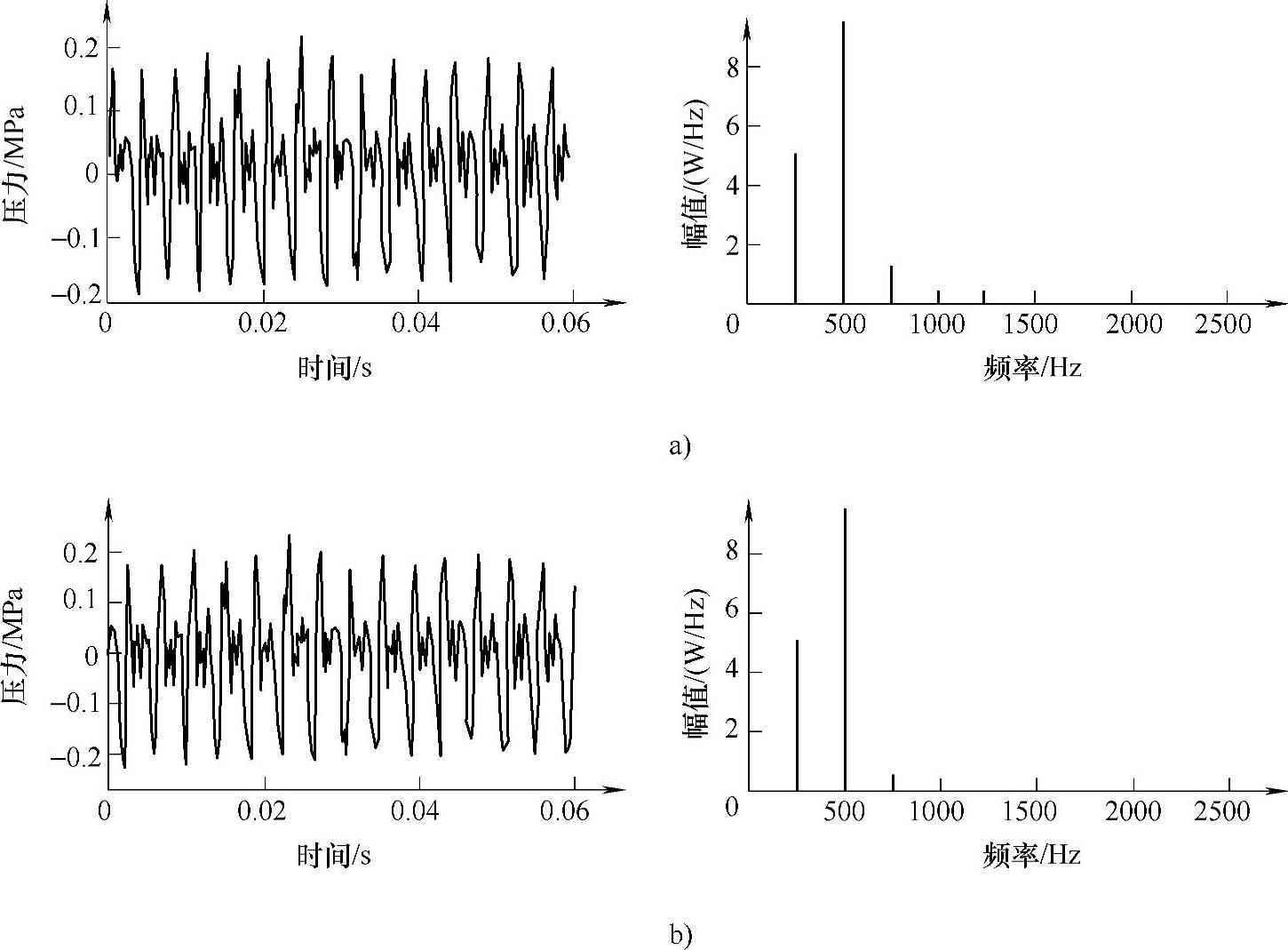
图3-17 压力脉动特征频带重构结果及其功率谱(www.xing528.com)

a）正常状态 b）齿轮磨损

可见，压力信号脉动频率功率谱的啮合频率及其倍频处的谱线可以作为齿轮泵故障的识别特征。

（4）基于脉动模型的故障特征提取 除了直接检测液压设备压力信号进行故障特征提取之外，还可以通过压力信号间接进行故障特征提取的方法，即基于脉动模型的故障特征提取方法。对液压泵源而言，其脉动特性除受条件工况（稳态出口压力、工作介质和转速及摆角等）影响外，主要由液压泵内部结构特征所决定（运动机构类型、配流机构、摩擦副间隙、流道结构及相应几何尺寸等），是液压泵的固有特性。液压泵源等效脉动模型如图3-18所示，即等效流量q_V及等效阻抗z_V的频域模型描述，其中q_V反映了导致流量脉动的各种因素，z_V反映了液压泵内部液阻、液感、液容的综合阻抗效应。因此，脉动参数与液压泵源结构参数具有确定的对应关系，它们的测量及辨识有多种方法。

液压泵的脉动模型是泵的内在机理和规律的反映，既能全面反映泵本身的结构参数和工作状态，又与泵的负载动态特性无关，且比振动信号、温度信号更深入和更直观，具有明显的物理意义。q_V和z_V模型参数的辨识是依据泵的出口管路上任意两点的压力信号获得的。

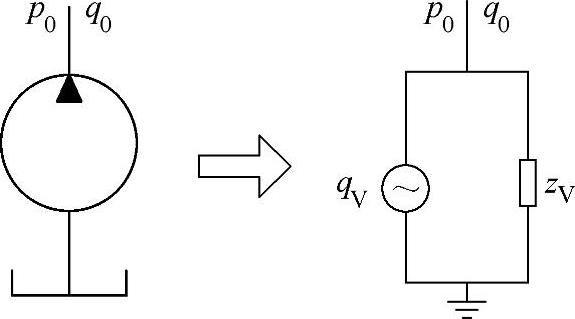
图3-18 液压泵源等效脉动模型

假设泵的出口压力和流量分别是p₀、q₀，按照管路的动态特性基本方程，泵出口任意两点的压力和流量分别为p₁、q₁和p₂、q₂，则有

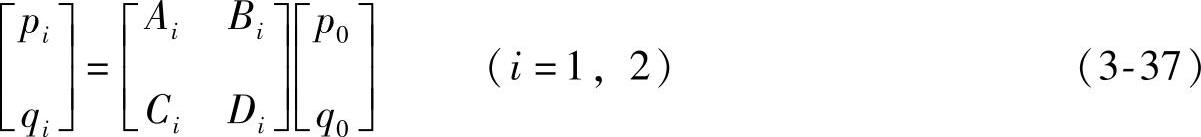
式中，A₁、B₁、C₁、D₁和A₂、B₂、C₂、D₂是按照频率相关模型得到的管路传递矩阵元素：

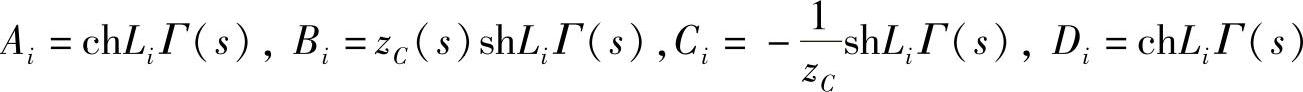
式中，Γ（s）=γ（s）l为管路的传播算子；γ（s）为管路的传播常数；L_i为管路长度；z_C为管路特征阻抗。

解式（3-37）可以得到液压泵的脉动模型：

根据动态负载不同的两套系统的出口管路压力信号，可以求出液压泵脉动模型的主控参数q_V和z_V。图3-19为主监测参数q_V和z_V的特性曲线。

液压泵源故障大多数会导致泵源内部结构参数变化，从而引起脉动参数相应改变，通过监测q_V、z_V的变化便可确定工作状态下泵结构参数的变化，判断发生变化的部位、性质和程度，从而实现泵源故障诊断。因此，采用液压泵源脉动模型作为监控模型，q_V、z_V作为主监测参数是液压泵故障诊断的一种可行方法。

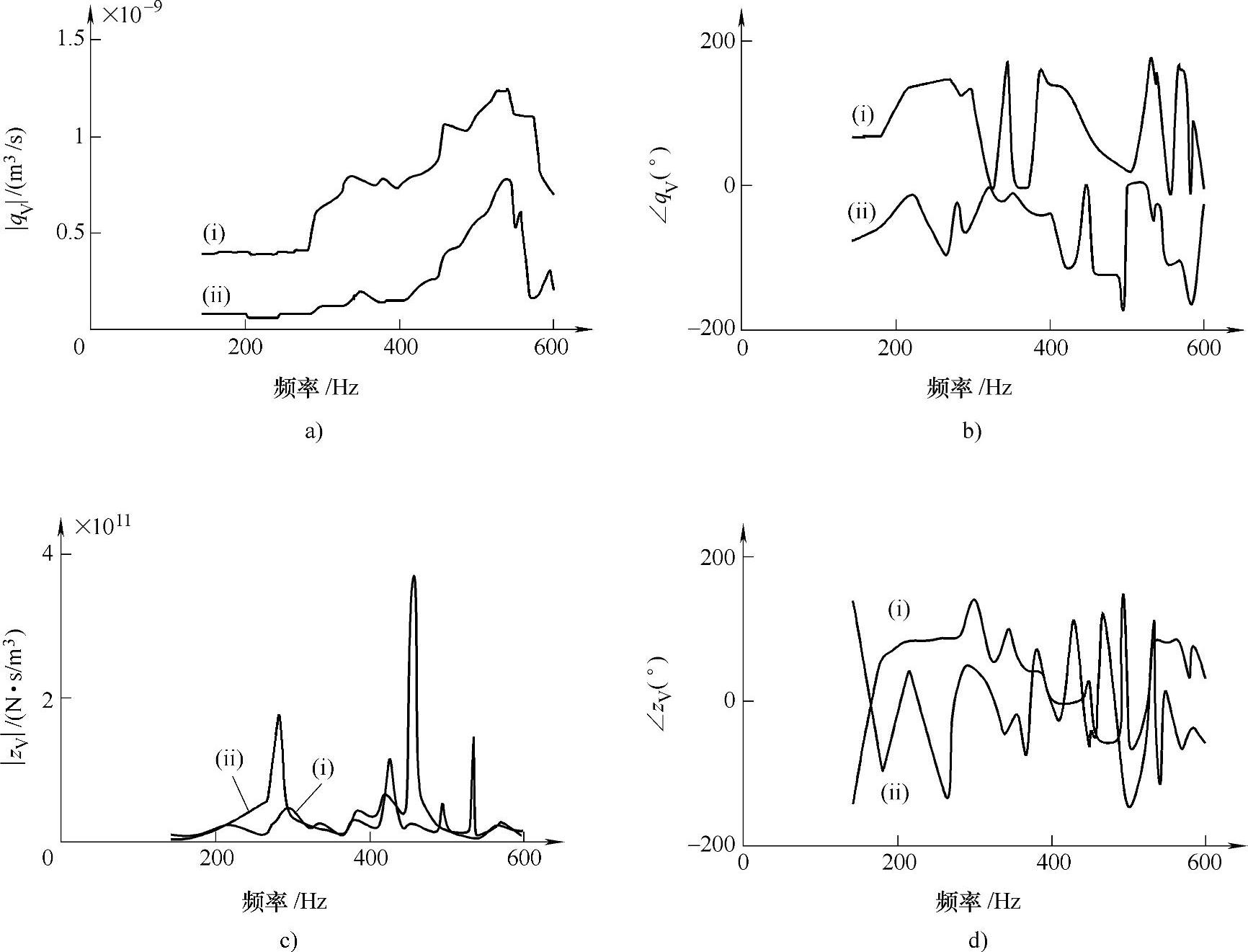
图3-19 主监测参数q_V和z_V的特性曲线

a）主监测参数q_V的幅值特性曲线 b）主监测参数q_V的相位特性曲线 c）主监测参数z_V的幅值特性曲线 d）主监测参数z_V的相位特性曲线 （i）为正常泵 （ii）为故障泵（柱塞球头松动）