经验模态分解法的探究与应用

傅里叶变换是建立在信号的平稳性假设上，而实际液压系统采集到的信号常常是非平稳非线性信号。这些非平稳非线性的信号中包含着丰富的故障信息，由于傅里叶变换本质上的缺陷，使提取的故障特征有缺陷，从而影响了设备的诊断。因此只有采取先进的时频分析方法，才能对液压系统的非平稳非线性信号进行较好的分析和故障特征提取。经验模式分解法是一种能够把时频信号分解成一系列固有模态函数的方法，该方法是由美国国家宇航局的Norden E.Huang于1998年首次提出的，该方法被认为是近年来对以傅里叶变换为基础的线性和稳态谱分析的一个重大突破。由于时间序列的信号经过经验模式分解^[16，17]（Empirical Mode Decomposition，EMD）成一组固有模态函数（Intrinsic Mode Function，IMF），而不是像傅里叶变换把信号分解成正弦或余弦函数。因此，此方法既能对线性稳态信号进行分析，又能对非线性非稳态信号进行分析。此方法已用于地球物理学、生物医学等领域的研究，并取得了较好的效果。

根据经验模态分解理论，满足以下两个条件的函数称为一个固有模态函数^[18]：①整个数据序列中极值点数目与过零点的数目必须相等，或至多相差一个；②在任意时刻，由局部极大值确定的包络线与由局部极小值确定的包络线之间的均值为零。

固有模态函数是理论意义上的单组分函数，亦即仅具有一个频率成分的函数。它代表涵盖于数据内部的振动模态，在每个波动周期内由零交叉点确定的固有模态函数仅包含一个振动模态，而不含有其他复杂的畸波。并且一个固有模态函数不只局限于一个窄带信号，它既可以是调幅信号，也可以是调频信号，同时也可以是调频调幅信号。它能够满足很多其他后继的时频分析方法需要的条件，如Hilbert变换、魏格纳-威尔分布等。这些时频分析方法，在该方法出现之前，虽然也有广泛应用，但出现的分析结果不尽人意。因为出现了很多虚假的频率成分，严重干扰了分析结果；更有甚者，得到的分析图像根本无法得出有意义的结论。但实际上，经验模态分解得到的各固有模态函数并不是绝对完全符合上述固有模态函数的定义，而是一种近似。

上述的第一个条件与传统的稳态高斯过程的窄带要求类似，它保证了该数据序列的局部极大值总是正的，而局部极小值总是负的。第二个条件则是一个全新的概念，它将传统的分析数据序列的全局条件转变为依据数据序列自身特性的局部条件，亦即将传统傅里叶分析中的全局分析转变成局部分析，这样就起到了自适应滤波器的作用。因为对于非平稳数据而言，采用“局部时间尺度”的概念计算“局部平均”是不可能的，因此条件②采用数据极大值与极小值的局部包络均值代替“局部时间尺度”，使数据的波形局部对称，这样就满足了具有物理意义的瞬时频率的一个必要条件——函数相对于零均值对称。虽然采用这种近似时求得的瞬时频率不可能适合任何条件，但经过实际应用表明，即使在最坏的条件下，这样确定的瞬时频率仍然具有所研究系统的物理意义。

对于任意一个数据序列x（t），采用经验模态分解法即可得到各阶的固有模态函数^[19]：

1）初始化：r₀（t）=x（t），i=1。

2）提取第i个固有模态函数（IMF）。即①初始化：h₀（t）=r_i（t），k=1；②提取h_k-1（t）的局部最大值与局部最小值；③采用三次样条对局部最大值与局部最小值进行插值，分别形成h_k-1（t）的上包络线与下包络线；④计算h_k-1（t）的上下包络线的均值m_k-1（t）；⑤如果满足固有模态函数（IMF）准则，就令IMF_i（t）=h_k（t），否则转到②，并且k=k+1。

3）定义：r_i（t）=r_i-1（t）-IMF_i（t）。

4）如果r_i（t）仍然具有至少两个极值，则转到2），并且令i=i+1；否则分解过程完成，而r_i（t）是x（t）的“残余量”。

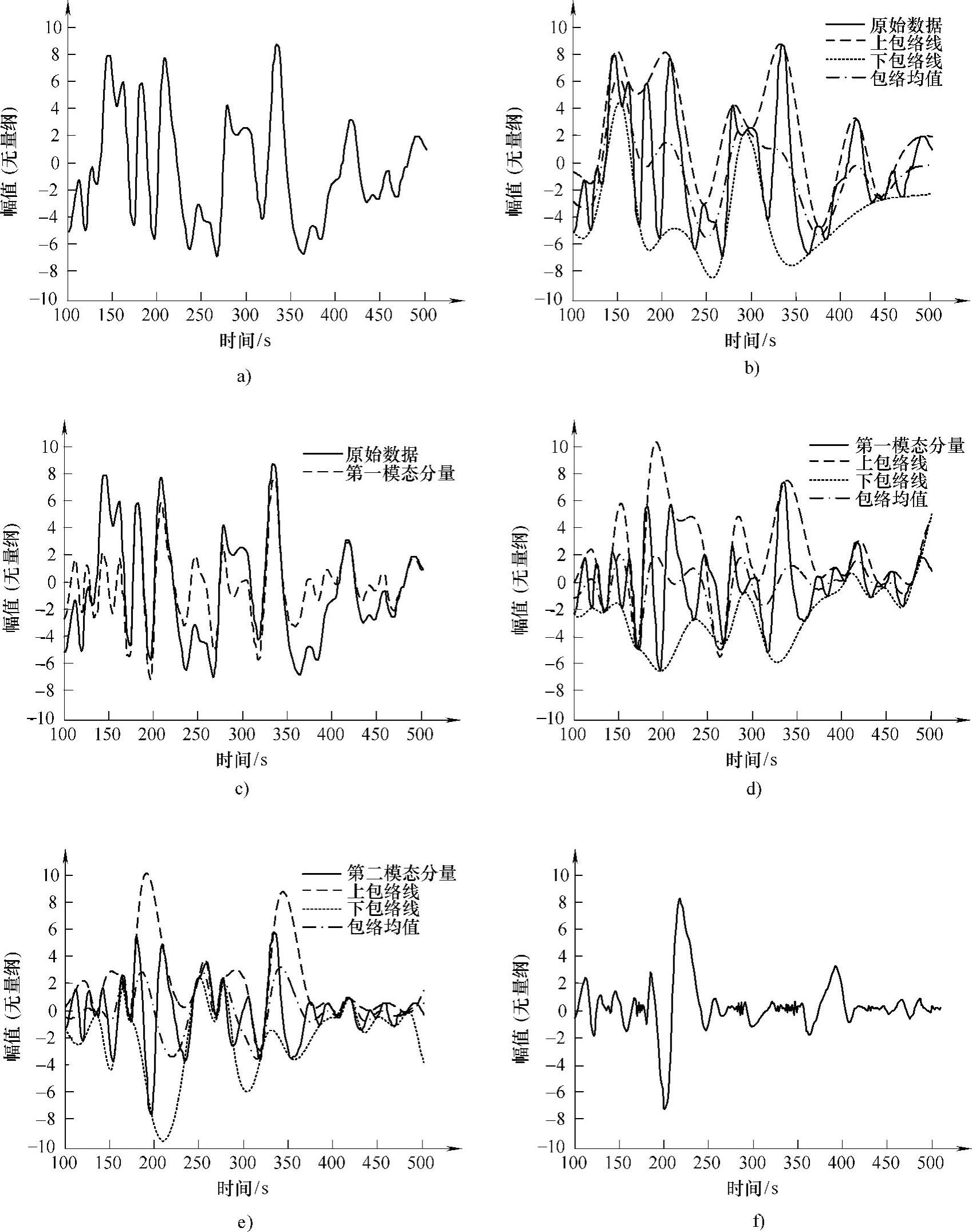
首先，原数据序列x（t）初始化为r₀（t）。该初始化可以看成引入外循环而将输入信号分解成连续的各个固有模态函数。第二个内循环则是开始寻找每个单一的固有模态函数（IMF）。该循环再一次由前述的过程初始化，即令r_i作为内循环的开始序列。内循环的第一次运行，即k=1，此时h_k-1（t）相当于原始数据序列x（t）。信号的各极值随后提取出来。然后由三次样条连接的各极小值与极大值分别形成了原始数据序列x（t）的下包络线与上包络线。则其相应的均值m_k-1（t）定义为上包络线与下包络线之差，并从原始数据序列h_k-1（t）中减去，从而得到一个临时的第一个固有模态函数h_k（t）。随后就确定该临时的固有模态函数是否满足真正意义上的固有模态函数的条件。一般而言，经过第一次运行该算法后，所需要的判断准则是不满足要求的，因此，通过采用h_k（t）对h_k-1（t）（因为k=k+1）进行初始化，而从②开始进行下一次的内循环。直到停止准则完全满足要求，才能停止这样的内循环过程。这就是Huang等人提出的称为“筛”的过程，它就像筛子一样，将不满足条件的数据序列滤掉，而将满足条件的数据序列留下并存储起来。这样，第一层固有模态函数（IMF）就被分解出来，倘若仍不满足外循环的停止准则，则整个过程重新进行，以从数据序列x（t）中筛选出其余的IMF。经验模态分解过程如图3-11所示，从中可以更清晰地理解Huang所提出的经验模态分解过程。

(www.xing528.com)

图3-11 经验模态分解过程

a）原始测试数据 b）数据上下包络线及其均值 c）原始数据与第一次筛选后得到的数据 d）重复筛选中的上下包络线与均值 e）第二次重复筛选的上下包络线及均值 f）多次筛选后得到的第一个IMF

当外循环的停止准则满足要求时，就中止这样的迭代分解过程，此时r（t）可以认为是数据序列x（t）的“残余量”，它也可以表示该信号的趋势，也可以称其为信号的“趋势项”。它在瞬变信号的分析中基本不具有分析作用，所以一般都将其去掉。

经过信号的筛选过程，原始信号x（t）可以表示为一定数目IMF及残余项的和，即

式中，n是IMF的数目；r（t）是筛选过程停止的最终残余量。这样就获得了n个固有模态函数和一个残余信息量。从经验模态分解法的步骤可以看出，每层IMF与该层提取前的IMF相比，包含了更低的频率成分，这样IMF代表了原始信号中包含的不同时间尺度的特征信号，残余量r（t）代表了原始数据中的趋势量信息。这一特性可以很好地用于检测快速的频率变化，这是因为该变化在每一层的固有模态函数上将有清晰的体现。

总结基于振动信号的故障特征提取方法可以看出，无论采用时域方法、频域方法、时频域方法还是经验模态方法，其故障特征频率仅有以下两种可能性：

1）特征频率为精确的分频或倍频振动。从故障机理上来讲，发生以上情况的主要原因是故障振动频率由激励引起，故障振动主导频率取决于激励力（或位移）。旋转机械的故障振动主导频率往往是精确的同频或倍频。另外，系统的动力特征变化也会引起故障振动频率，其主导频域大多与转速的精确倍频或分频有关。

2）特征频率为非精确分频和倍频振动。旋转机械发生故障时会出现与非精确分频或倍频相关的特征频率，其主要原因是流体激振和转子上零部件松动或轴承产生滑差等。