时频域故障特征提取方法优化

振动信号包含丰富的冲击成分，呈现典型的非平稳时变特征，需从时域和频域两方面综合描述振动信号才能有效提取故障特征信息，这正是小波分析的重要特性。小波变换在时域和频域均具有良好的局部化性质，可用多重分辨率来突出信号局部特征，适用于探测正常信号中夹带的瞬态反常现象并展示其成分^[12，13]。

小波分析是一种窗口大小（窗口面积）固定但形状可变、时间窗和频率窗均可改变的时频局部化分析方法，即在低频具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率。连续小波分解的原理如图3-7所示。

对于图3-7中的连续小波分解，小波分解系数为

C（scale，position）=∫^∞_-∞f（t）ψ（scale，position，t）dt （3-27）

式中，f（t）、ψ（scale，position，t）分别为原始信号函数；小波函数scale为分解的尺度。

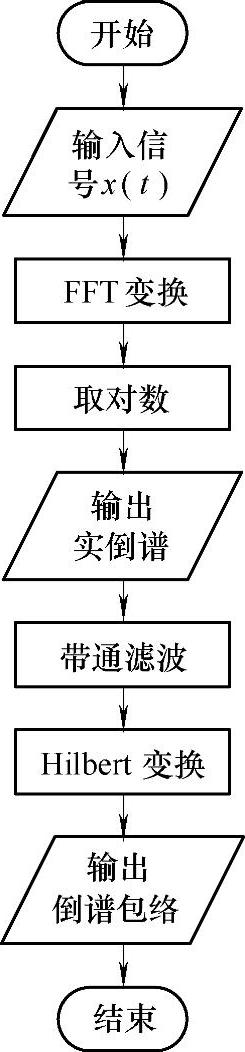
图3-6 倒谱包络分析流程

小波分解与傅里叶变换的区别是小波分解是利用具有紧支结构的小波函数进行分解，分解出来的信号是具有不同尺度（频率特性）和时间的各种小波函数；而傅里叶变换是利用正弦函数进行分解，分解出来的信号是不同幅值和频率的正弦函数。因此小波分解可以得到信号的频率特性，同时也可以得到信号的时域上的特性。这个特性对于故障诊断尤为重要，它可以得到出现故障的时间点，同时对于随机信号的分析比傅里叶分析要好。小波分析包括：

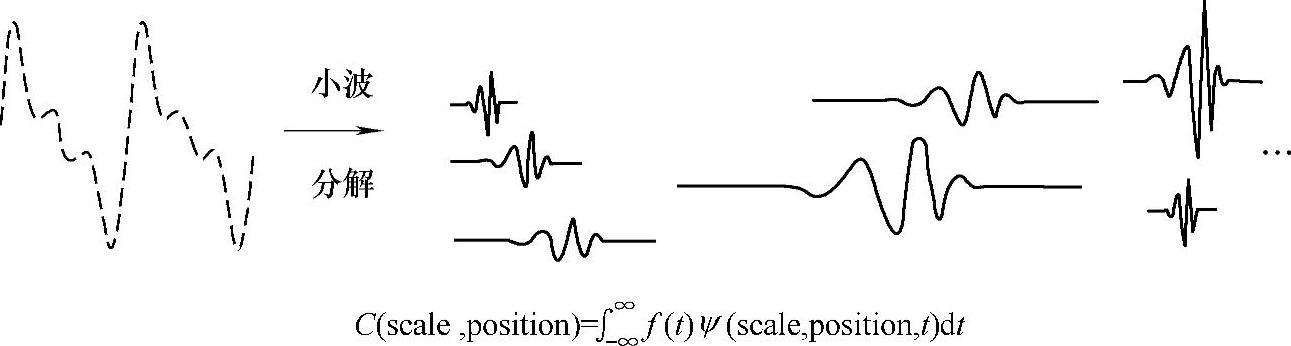
图3-7 连续小波分解原理示意图

（1）小波包分解 小波包分解的过程是信号低通滤波和高通滤波的过程，如图3-8所示，它可以在整个时频域中进行分析，获得更多的参数特征。

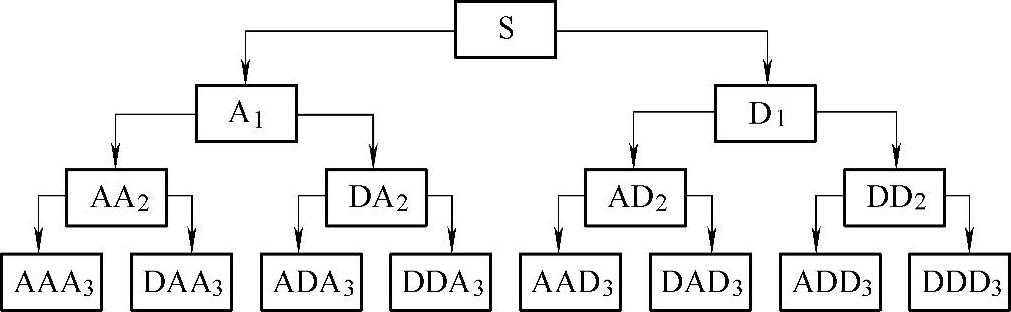
图3-8 小波包分解

信号的小波包分解：

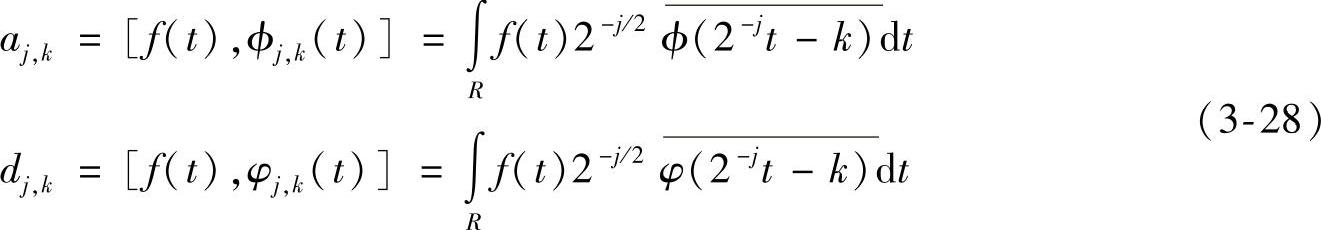
式中，f（t）为信号函数；ϕ（t）为小波函数；φ（t）为尺度函数；j为分解的尺度；k为平移因子；R为信号的积分区间；a_j，k、d_j，k分别是尺度j上的第k个低频和高频分解的小波系数。(www.xing528.com)

f（t）的离散信号为f（n），n=1，2，…，N。f（n）表示信号在尺度j=0上的近似值，记为c₀（n）=f（n），则f（t）的离散小波包分解为

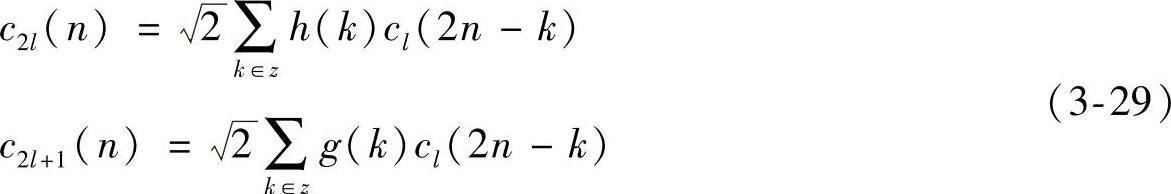
式中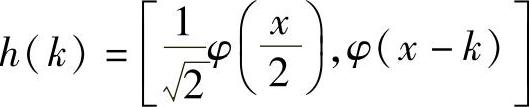，；g（k）=（-1）^kh（1-k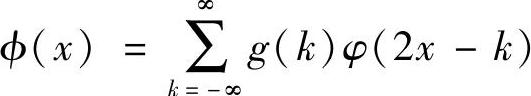）；；c_2l、c_2l+1分别为小波分解的低频系数和高频系数；在尺度j=J上分解的序列为。

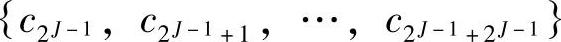小波包分析能够为信号提供一种更加精细的分析方法，能够将信号进行多层次的划分，对分辨率没有细分的高频部分进行进一步的分解，能够根据被分析的信号的特征，自适应的选择相应的频带。从而提高信号的时-频分辨率，这点对于故障诊断更具有价值。

（2）小波包分解系数重构 信号小波分解的矩阵表示形式为

则小波包分解后的重构信号为

c_j（k）=H^∗c_j+1+G^∗d_j+1 （3-31）

式中，H^∗、G^∗分别为H、G的对偶算子；分解后的信号一步步地恢复出原始信c₀（n）=f（n）。

图3-9 小波包分解和重构的示意图

如图3-9所示为小波包分解和重构的示意图。利用小波包分析对信号进行消噪处理，这是小波包分析的最基本的应用。在工程实际中，有用的信号通常表现为低频信号或是一些比较平稳的信号，而噪声信号通常表现为高频信号。所以将信号进行小波包分解，对分解的小波包系数进行阈值量化，重构量化后的系数，得到新的去除了部分噪声的原始信号。具体的方法是：①信号的小波包分解，选择一个小波并确定一个小波分解的层次N，然后对信号进行N层小波包分解；②确定最佳小波包基；③对小波包分解系数的阈值量化。对于每一个小波包分解系数（特别是低频系数），选择一个适当的阈值并对系数进行阈值量化；④小波包重构。根据第N层的小波包分解系数和经量化处理的系数进行小波包重构。

经过以上处理后的重构信号，消除了部分噪声，对于机械故障诊断提取特征信号尤为重要，特别是对于液压泵的故障诊断^[14，15]。如图3-10所示为液压系统振动信号及其小波消噪效果，即采用小波分析和未采用小波分析的比较，很显然小波分析可以有效剔除环境干扰，当液压系统出现故障时有利于凸显故障特征。

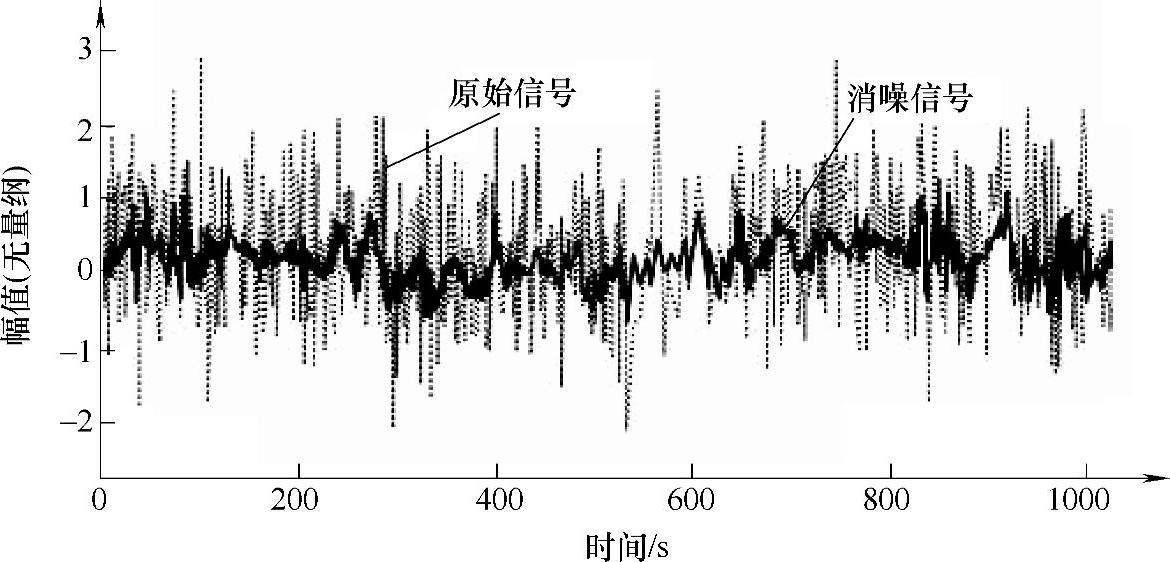
图3-10 液压系统振动信号及其小波消噪效果