如何通过倒谱包络进行液压系统故障特征提取？

当液压系统的故障信号通过传输通道到达故障检测传感器时，要进行有效的振动故障特征提取需要剔除传输通道的干扰，因此倒谱包络方法应运而生。对于液压泵轴承故障的微弱特征信号提取，倒谱包络是行之有效的方法^[11]。倒谱包络算法包括以下三个部分：

（1）求解倒频谱模型 假设液压系统上检测到的信号为x（t），它是故障信号经传输后的信号，f（t）为故障激励信号，h（t）为传输通道的脉冲响应。其相应的傅立叶变换为X（w）、F（w）和H（w），则有以下关系：

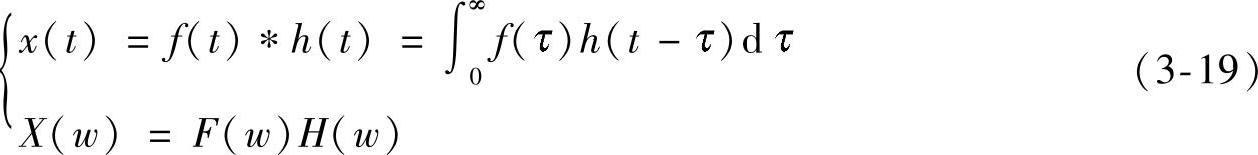
对式（3-19）作如下变换：

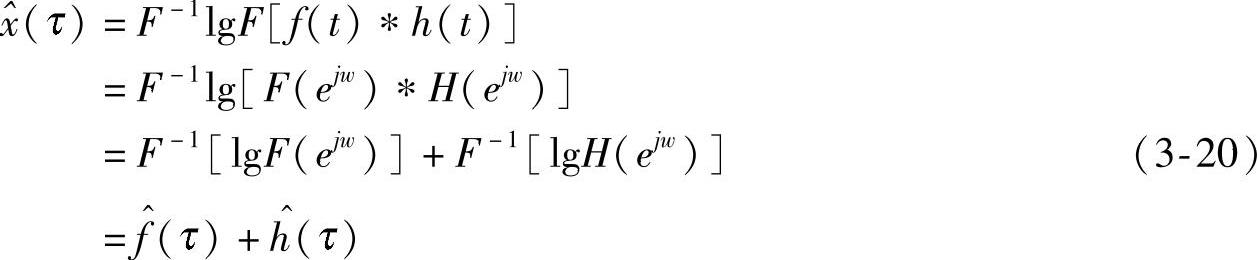
式中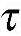，为倒频率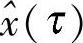；为倒频谱。

由式（3-20）可以看出故障激励信号和传输通道的特性被分离了，而一般情况下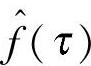和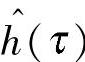信号占据不同的倒频区段，所以这样可以突出故障信号的特性。

（2）包络分析的实现 包络的原理是利用系统的传递特性，采用滤波和解调技术，提取故障特征频率分量，从而突出故障信息，提高信噪比。其原理如图3-5所示。

（3）Hilbert变换和包络提取 Hilbert变换主要用于信号分析中求时域信号的包络，以达到对功率谱进行平滑从而突出故障信息的目的。

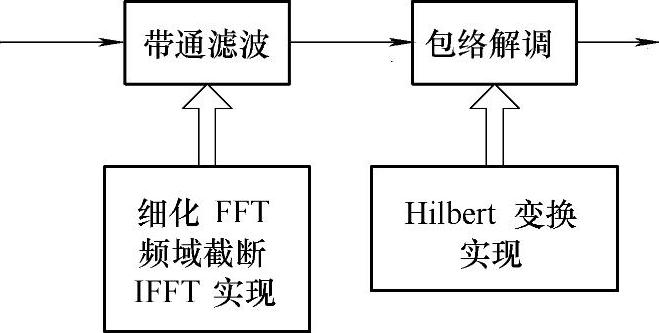
图3-5 包络分析原理

假设给定信号x（t）为连续的时域信号，其Hilbert变换的定义如下：

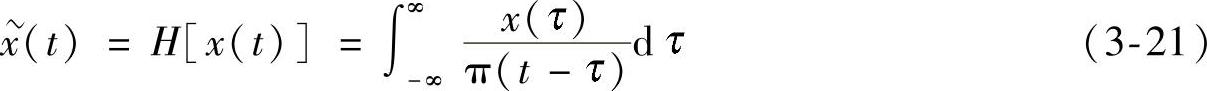
两边取傅里叶变换：(https://www.xing528.com)

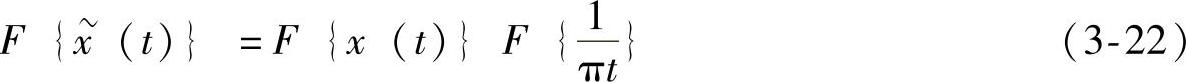
在定义符号函数sgn（t）的傅里叶变换后：

由傅里叶变换的对称性，有

可以将式（3-22）写成：

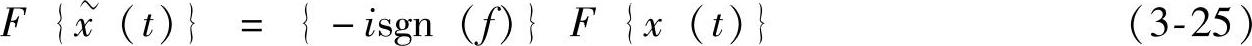
结合Hilbert变换结果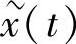，可以得到信号包络如式（3-26）所示：

式中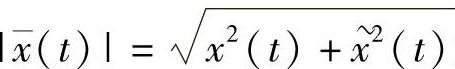，为最小意义上的最佳包络。

倒谱包络模型的实质是对从传感器获得的信号进行倒频谱分析，然后对其倒频谱信号进行包络提取，从而双重性地突出了故障信息，为信噪比小的故障特征的提取依据。

倒谱包络是一种非常有效的故障特征提取方法，该方法的分析流程如图3-6所示。