频谱分析法：旋转机械振动故障特征提取常用方法

所谓频谱分析就是将信号强度按频率顺序展开，使其成为频率的函数，并考察变化规律。频谱分析的目的是把复杂的时间历程波形，经过傅里叶变换分解为若干个单一的谐波分量来研究，以获得信号的频率结构及各谐波相位信息。旋转机械振动故障特征提取常用的方法是频谱分析法，即根据振动信号的频率成分大致判断出故障的原因。对旋转机械进行频谱分析时，一般都把振动故障特征频率描述成与基频、倍频或二分之一频相关的振动，如柱塞液压泵的柱塞游隙增大故障发生时，会在上死点和下死点附加发生异常振动，因此其故障特征频率为轴频率的2倍。齿轮泵发生转子不平衡、轴承故障和齿轮故障分别对应的振动频率，即不同的频率的振动故障有可能来自不同的故障原因，图3-4为信号的时域和频域图。

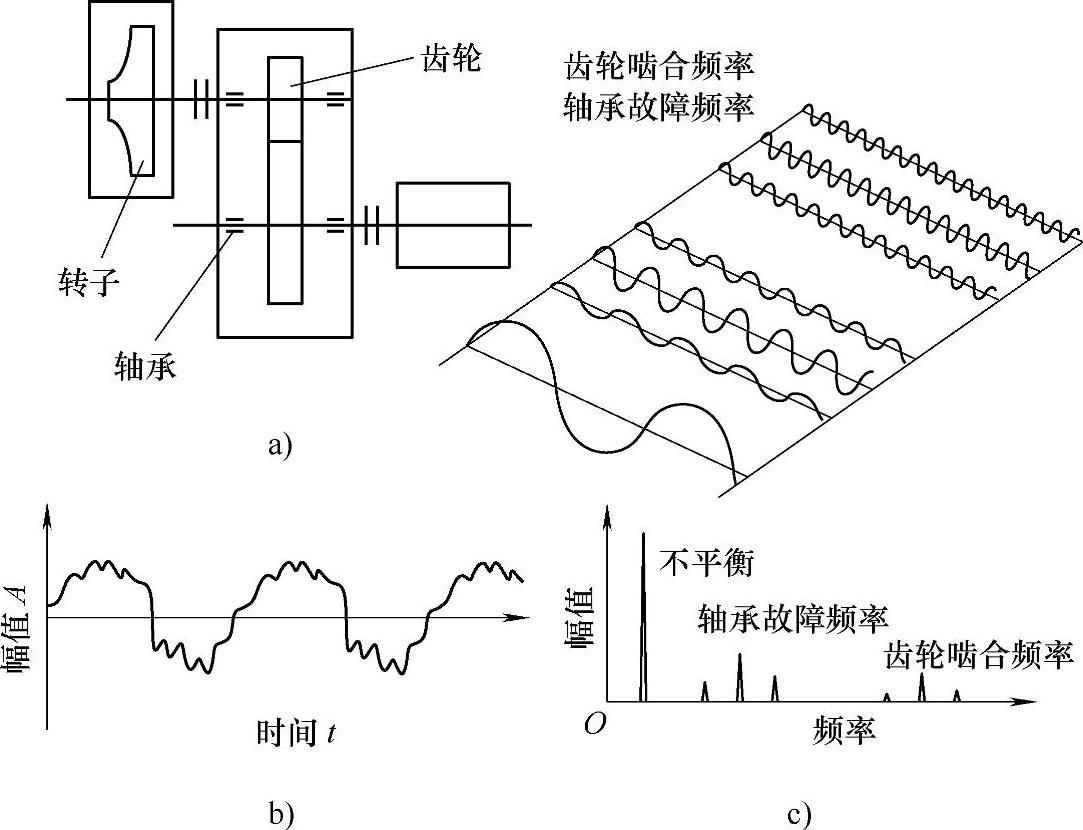
图3-4 信号的时域和频域图

a）故障频率产生的原因 b）表面振动信号的时域波形 c）表面振动信号的频域波形

假设一个简单振动的频率是f₀（基波），另一个简单振动的频率为2f₀，一个设备同时经历这两种振动，便形成一个复杂的振动。当研究振动幅值A随时间t变化时（图3-4a），发现该振动是一个叠加振动信号，可以从振幅-时间来观察（图3-4b）两个波形，也可以将信号进行傅里叶变换得到其频谱图（图3-4c）。

（1）故障的振动主导频率与激励的关系 对于强迫振动，响应是由激励引起的，故障振动的主导频率取决于激励力（或位移）。假设激励力为复杂的周期函数F（t），可以采用振动理论的谐波分析方法，把周期函数F（t）展开为一个傅里叶级数：

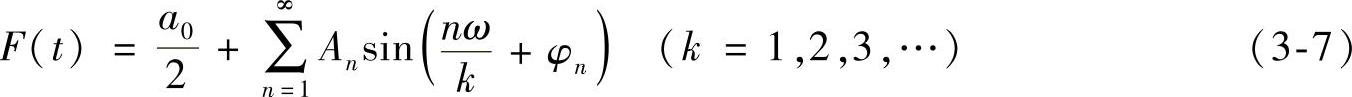
当n=k时，振动角速度ω相当于设备的旋转角速度，此时为同频振动；n＜k为次谐波振动，即分频振动；n＞k为倍频谐波振动。

不同的旋转机械有不同的故障振动主导频率，例如液压泵的轴频率为

式中，N为液压泵转速；f₀为轴频率。

（2）故障振动主导频域与系统动力特征的关系 故障振动的主导频率也取决于系统本身的动力特征，系统的动力特征矩阵为

[z（ω）]=[k]-ω²[m]+jω[c] （3-9）

系统动力特性在液压元件运行中有时也会发生变化，如支承轴承的总刚度系数为

式中，k_p为油膜刚度系数；m_b、k_b分别为支承轴承及基础的等效质量和等效刚度系数。

k会随设备转速、油膜温度等发生变化，从而造成自激振动。振动故障的主导频率有时也与转速有关，这是因为系统刚度、质量、阻尼的变化在某些场合与转速关联。

功率谱法的实质是从诊断参数能量变化的角度对设备进行故障诊断，它是故障诊断频域分析方法的一种，比较成熟、有效。它经常用在旋转机械（如液压泵）的故障诊断上^[10]。

定义自功率谱：(www.xing528.com)

S_x（f）=∫^∞_-∞R_x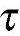（）e^-j2πftdt （3-11）

由R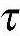（）的定义得

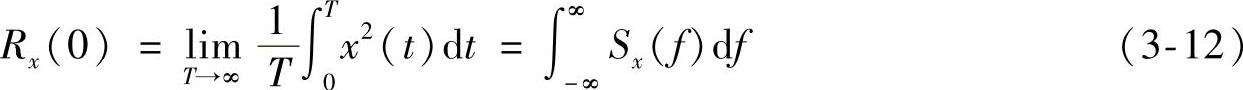
易知S_x（f）曲线与频率所围面积为信号平均功率，故S_x（f）为单位频率上的平均功率。

从能量的概念出发，根据巴塞伐定律，一个函数x（t）的总能量为

∫^∞_-∞|x（t）|dt=∫^∞_-∞|x（f）|df=∫^∞_-∞x（f）x^∗（f）df （3-13）

所以函数x（t）的能量谱密度函数为

E[f]=x（f）x^∗（f）=|x（f）|² （3-14）

其中，

x（f）=∫^∞_-∞x（t）e^-j2πftdt （3-15）

当函数x（t）具有能量谱时，则x（t）为平方可积函数，即

∫^∞_-∞x（t）x^∗（t）dt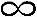＜ （3-16）

因此，若x（t）的谱x（f）包含有一个或数个σ函数，即x（t）包含有正弦和余弦等周期信号时，积分值不可能小于正无穷，上式就不能成立，所以周期信号不能用能量谱表示。对那些非平方可积的函数，如周期函数来说，若其均方值满足下述极限式：

则存在功率谱密度函数，使系统中能量传递的平均功率为有限值，该功率谱函数可表示为

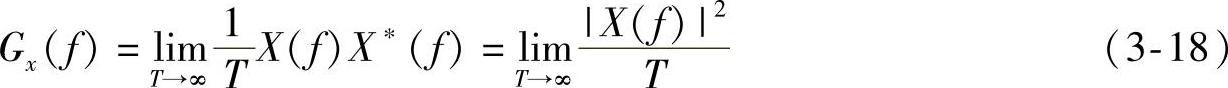
式（3-18）表明功率谱是整个时间过程中单位时间、单位频率间隔中的能量的平均值。功率谱适用于周期信号、随机信号和阶跃函数的谱分析，而能量谱更适用于非周期信号，特别是瞬态冲击信号的谱分析。