一般认为失效是一种二元状态，即某产品正常或损坏，然而实际工况下失效过程要比二元状态复杂得多，失效是作用在产品上的应力与产品材料、组件交互作用的结果。一般产品所承受的应力与产品材料的变化是随机的，因此要想正确理解产品的失效进程，需要充分分析产品材料、组件与应力的响应。常用的四个失效简化模型如下[3]。
1.应力-强度模型
当产品承受的应力仅超过所允许的强度时，产品才会失效。一个未失效的产品就像新的一样，如果应力没有超过所允许的强度，应力无论如何都不会对产品造成永久性影响。这种失效模式更多地取决于环境中关键事件的发生，而不是时间或循环历程。强度被视为随机变量，可用这一模型的有钢棒受拉应力、晶体管发射极-集电极间施加的电压等。
假设δ表示材料的强度，s表示受到外界的应力，它们都是随机变量，其密度函数分别为f（s），g（δ），则产品的故障累积概率可以表示为[3]
F=1-∫∞-∞f（s）[∫∞sg（δ）dδ]ds=∫∞-∞Gδ（s）f（s）ds （2-1）
或
F=1-∫∞-∞g（δ）[∫δ-∞f（s）ds]dδ=∫∞-∞[1-Fs（δ）]g（δ）dδ （2-2）
式中，Gδ（s）=∫s-∞g（δ）dδ；Fs（δ）=∫δ-∞f（s）ds。
2.损伤-韧性模型
应力可以造成不可恢复的累积损伤，如腐蚀、磨损、疲劳、介质击穿等。累积损伤不会使产品使用性能下降。当损伤仅超过所允许的韧性时，也就是损伤累积到物体的韧性极限时，物体才会失效。当应力消除时，累积损伤不会消失，韧性经常被看成是随机变量。有许多机械零件如轴承、齿轮、密封圈、活塞环、离合器以及过盈连接等，它们构成不同形式的摩擦副，在外力作用下，有的还受热力、化学和环境变化的影响，经过一定时间的磨损而出现故障。
假设磨损量w是随着时间的增加而增大的，并且材料的磨损量和一定磨损量下的耐磨寿命服从随机的统计分布。试验和统计资料表明机械产品的磨损量和耐磨寿命服从正态分布、对数正态分布以及威布尔分布。设磨损量的概率密度函数为ft（w），耐磨寿命密度函数为fw（t），各函数的下角标分别表示给定的寿命或给定的磨损量。
假设磨损量的变化具有稳定性磨损过程，即磨损量与时间呈线性关系：
w=w0t （2-3）
式中，w0为单位时间的磨损量。
磨损量的单位可以是磨损尺寸或磨损体积，当零件的累积工作时间达到t时，零件的可靠度为：
R（t）=P{t（w）＞t}=∫∞tfw（t）dt （2-4）
式中，t（w）为零件磨损量为w条件下的耐磨寿命。
假设fw（t）服从正态分布，即
用
置换成标准正态分布：
式中，μt、σt分别为平均耐磨寿命和耐磨寿命标准差。
同样，如果给定规定时间t，按照磨损量分布密度预计零件的可靠度，那么在规定允许磨损量w时： (www.xing528.com)
R（t）=P{w（t）＜w} （2-7）
式中，w（t）是磨损时间达到t时零件的累积磨损量。
假设给定磨损时间t的磨损量密度函数ft（w）服从正态分布，即
用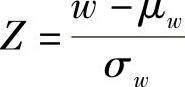
置换成标准正态分布：
式中，μw、σw分别为平均磨损量和磨损量标准差。
以上分析为理想情况，通常零件磨损量按照要求给定时间有一个允许的磨损分布ft（w∗），然而在实际的试验结果中，这种实测到t时间的磨损分布是服从另外参数的正态分布ft（w）。这两种正态分布的均值和标准差分别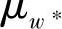为
、
和μw、σw，要求在任何情况下在t时间内满足w（t）＜w∗（t），这种情况类似于强度可靠性的干涉情况，随机变量y=w-w∗＞0的概率，即可靠度在t时间为
R（t）=P（w-w∗＞0）=1-φ（z） （2-10）
其中，
。
3.激励-响应模型
如果系统的一个组件坏了，只有该组件被激励时才发生响应失效，并导致系统失效。如汽车的紧急制动装置、大多数计算机程序或电话交换系均属于这种情况。这种失效模式更多取决于关键事件何时发生，而不是时间或循环历程[4]。
4.容差-规格模型
该模型用于仅当局限在规格范围内，系统的性能特征才能符合要求的情况下。任何性能质量渐进退化的部件和系统都属于这种模型。
设产品的设计参数为p1、p2、…、pn，其性能特征值Vi可以用如下关系式表示：
Vi=f（p1，p2，…，pn） （i=1，2，…，m） （2-11）
将式（2-11）在其名义值处按泰勒级数展开，取其第一项，略去高阶项可以得到性能特征值Vi的变化ΔVi与设计参数Δpj之间的线性表达式：
式中，∂Vi/∂pj为性能特征值Vi对设计参数pj的偏导数；下标“0”表示名义值；Δpj为设计参数pj的偏差。
利用式（2-12）可以求出ΔVi的正负极限值。
为了确定系统性能特征对各部件参数偏差的灵敏度Sij的影响，引入如下关系式：
从而得到灵敏度对应的性能特征值偏差ΔVi为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
