电弧故障检测中的频谱分析方法应用

电弧故障的过程随机性很强，且电弧故障的时域波形随负载类型及工作状态差别很大，较难提取到电弧故障过程的特征量。但根据电弧故障波形明显的频率特性，可尝试通过频谱分析，从频域的角度来对电弧故障过程进行分析，寻找并提取电弧故障过程中的频域特征，提高电弧检测的可靠性。上海电器科学研究所（集团）有限公司和上海电科电器科技有限公司近年来开展了电弧故障波形的频谱分析研究，采集了大量负载起动过程、正常运转和发生串联电弧故障时的电流波形，例如，各种类型节能灯、调光灯（晶闸管型）、卤素灯、计算机、电钻、吸尘器、空气压缩机、电吹风、空调器等负载的波形，并对其变化特征及其频谱进行分析，取得了有益的成果。

13.2.4.1 频谱分析的理论基础

信号的频谱分析理论建立在傅里叶变换的基础上。傅里叶原理指出：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅里叶变换算法利用直接测量的原始信号，以累加方式计算该信号中不同正弦波信号的频率、振幅和相位，将原来难以处理的时域信号转换成易于分析的频域信号（信号的频谱），可令某些杂乱无章的时域信号变得简洁且更利于后续分析。

由于计算机只能够处理离散的数字信号，进行频谱分析时，不仅连续的时域信号要被离散化，而且连频谱函数也要离散变换。通常把无限长的周期序列给计算机处理也是没有必要的，只需处理周期序列的一个周期的值就足够了。因此，最适合的方法是采用离散傅里叶变换（DFT）。

1.离散傅里叶变换

长度为N的有限长序列x（n）的离散傅里叶变换（DFT）的表示式为

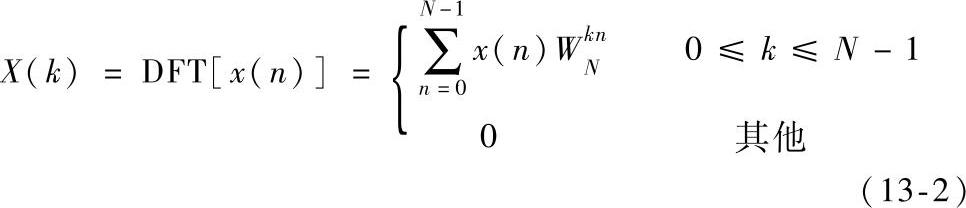
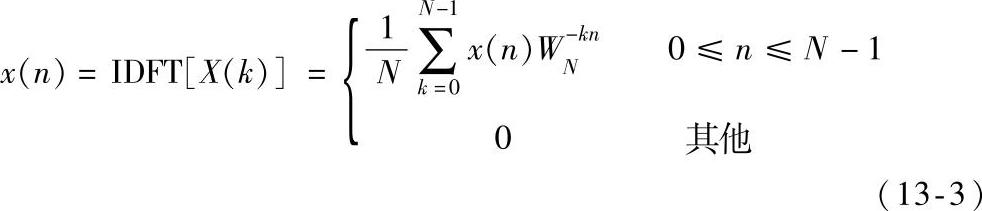
式中，。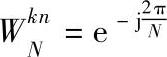

2.离散傅里叶变换参数的选择

利用DFT计算连续的时域信号（模拟信号）时需要注意的问题：

若信号最高频率为f_H，按照采样定理，采样频率f_S应满足

f_S≥2f_H （13-4）

其采样间隔为F₀（即频率分辨率），由其可得到时域函数的周期，即记录长度T₀为

由上式可知，信号的最高频率分量f_H与频率分辨率F₀之间存在着矛盾，若增加f_H，则时域采样间隔T必定减小，f_S必定增加，由于采样点数N满足下列关系：

所以，若N固定不变，F₀必定增大，这会导致分辨率下降。反之，若要提高分辨率（减小F₀），则会令T₀增加，当N给定时，T必定会增加（f_S减小），要想不产生混叠失真，则信号的最高频率分量f_H必定会减小。要想兼顾信号最高频率分量f_H与频率分辨率F₀，唯一的办法就是增加记录长度的点数N，即满足

3.频谱分析的步骤

（1）软件平台 采用MATLAB软件分析平台，具有数值计算速度快、图形化界面丰富等特点，便于分析。

（2）频谱分析参数的选取 分析过程中，采样率设置为f_S=500kHz；以50Hz的频率分辨率对0～250kHz范围内的信号进行频谱分析，基本可以分辨出信号50Hz以上的变化。若令频率分辨率满足：F₀≤50Hz，最小记录长度T₀≥1/F₀=0.02s，得到一个周期内记录的最小数据长度为N≥f_S/F₀=10000。最后实际采用的频谱分析参数见表13-1。

表13-1 串联电弧试验频谱分析参数

（3）用FFT计算信号的频谱

X（k）一般由实部X_R（k）和虚部X_I（k）组成，即

X（k）=X_R（k）+jX_I（k） （13-8）

（4）由X（k）求幅度谱X（k）、相位谱θ（k）和功率谱S（k） 一般需要根据实际分析进行选取。其中

（5）短时傅里叶变换（STFT） 考虑到不同时刻下，负载电流的频域特征可能存在变化，进行频谱分析时，为了清晰地观察各个时间段内信号频率的变化，实际采用短时傅里叶变换（STFT）对信号进行频谱分析，即以0.02s为单位间隔，将2s数据截断成100段，然后分别对每段信号进行傅里叶变换。

但是，对信号的截断处理过程中，往往会出现“频谱泄漏”的现象，为了抑止这种效应，通常都会对采样数据进行加窗处理。分析时，实际中采用的是汉宁（Hanning）窗，其表达式为

在分析过程中，对每段数据进行了高通滤波处理，滤除500Hz以下信号，防止低次谐波的干扰。

13.2.4.2 典型负载电流波形频谱分析的示例

对几种典型的负载和串联电弧故障的电流波形进行了频谱分析，其分析结果举例如下：

1.空调器电流波形的频谱分析

空调器型号为春雷牌KFR-32G，功率3200W（制冷），在制冷模式条件下进行测试。其正常起动和电弧故障过程中的电流波形见表13-2。起动制冷模式后，电流波形出现陡增，然后衰减并趋于稳定；发生电弧故障时，电流波形幅值存在明显波动，并伴有波形的缺失。

表13-2 空调器起动和电弧故障过程中的电流波形

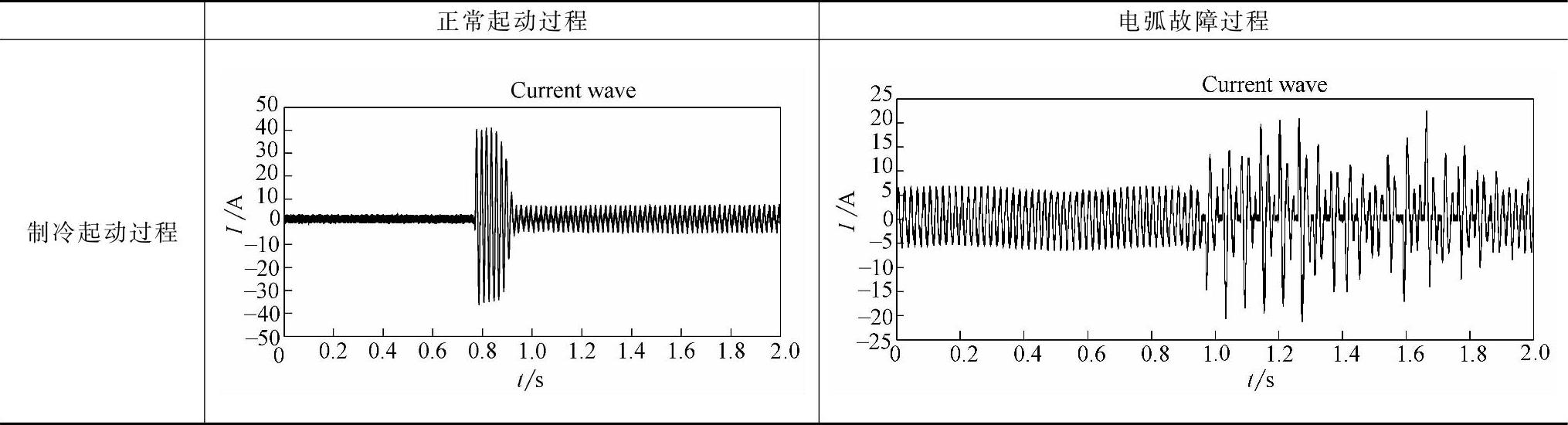
将空调器在起动过程中电流波形的100段数据进行短时傅里叶变换（STFT），得到起动过程的时频曲线频谱如图13-19所示。图中，X轴为频率轴，单位为Hz；Y轴为时间轴，单位为NT（单位周期）；Z轴为振幅轴。起动时刻前后平均STFT的结果曲线如图13-20所示（仅显示0～5kHz范围）。

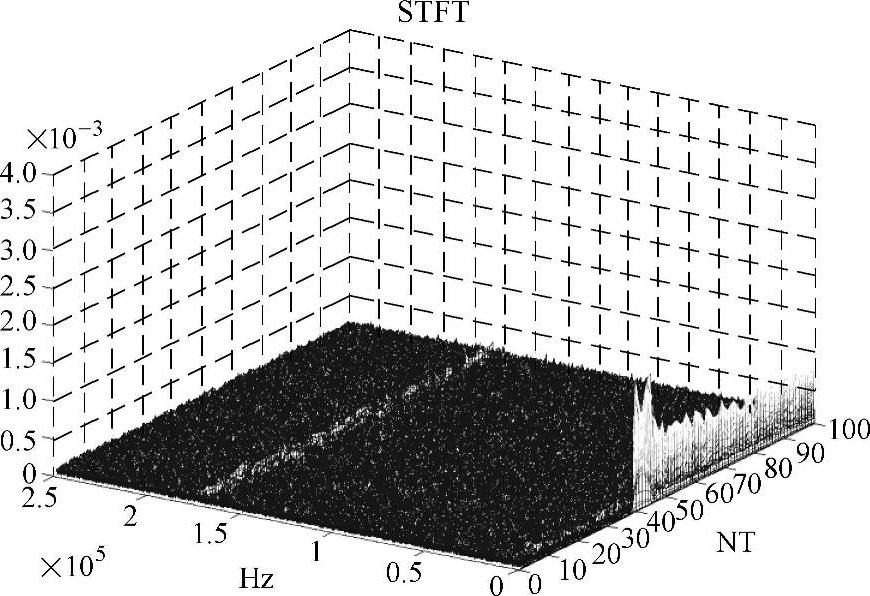
图13-19 空调器起动过程的时频曲线(www.xing528.com)

空调器发生串联电弧故障时频曲线以及电弧故障时刻前后平均STFT结果曲线分别如图13-21和图13-22所示（平均STFT仅显示0～5kHz范围）。在发生电弧故障后，空调器电流波形并没有出现较为突出的剧烈变化频率分量，只在其固定工作电流对应的频率分量处存在变化，即幅值出现波动变化，但其整体幅值水平在电弧故障前后并无显著增加。

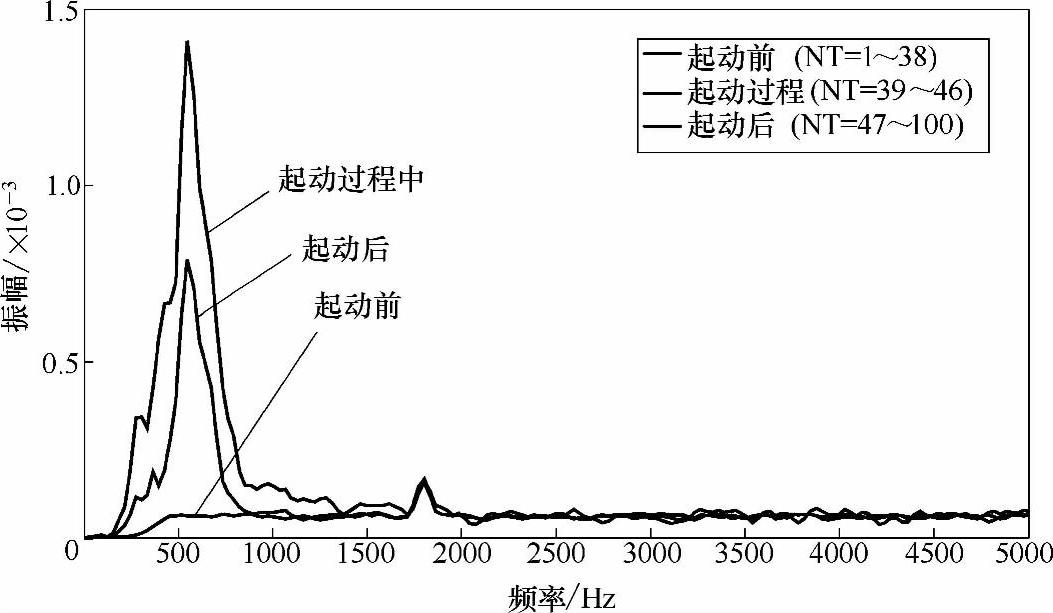
图13-20 空调器起动时刻前后平均STFT的结果曲线

图13-21 空调器发生串联电弧故障时频曲线

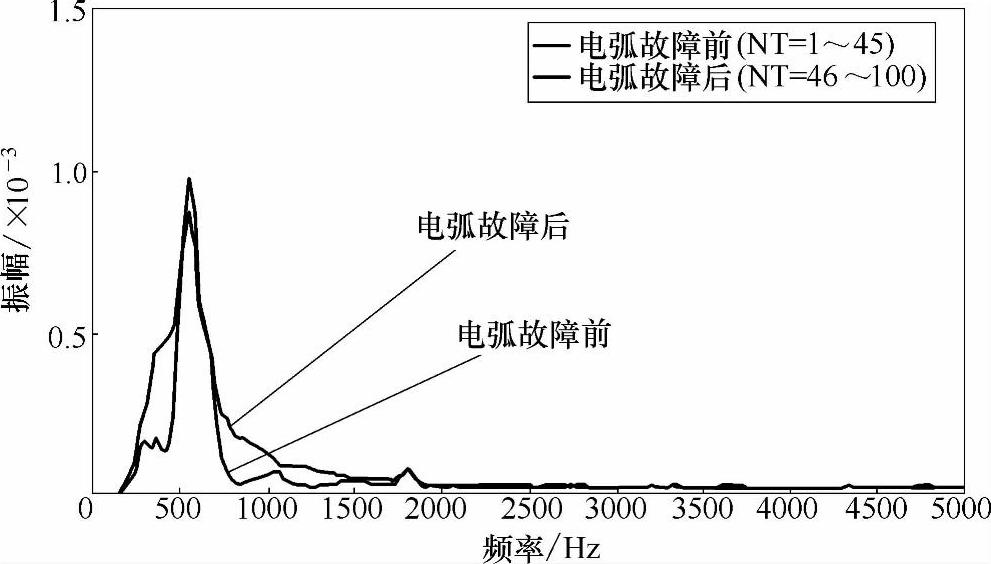
图13-22 空调器电弧故障时刻前后平均STFT结果曲线

2.卤素灯电流波形的频谱分析

卤素灯型号为PHILIPS公司的MR16，总功率为300W。卤素灯正常启动过程以及电弧故障过程中电流波形见表13-3。启动时存在明显的冲击电流，波形呈指数衰减，并趋于稳定；出现电弧故障时，卤素灯电流波形出现剧烈变化。

卤素灯正常启动过程中100个周期的STFT时频曲线及启动时刻前后平均STFT结果曲线分别如图13-23和图13-24所示。启动前的第1～29个周期内，无明显变化；在启动过程的第30～31个周期内，因冲击电流造成整个频带范围内均出现变化；在启动后的第32～100个周期内，频率波动趋于稳定，除存在主峰值约为500Hz的固定频率分量外，其余频段范围基本无明显波动现象。

表13-3 卤素灯电流波形

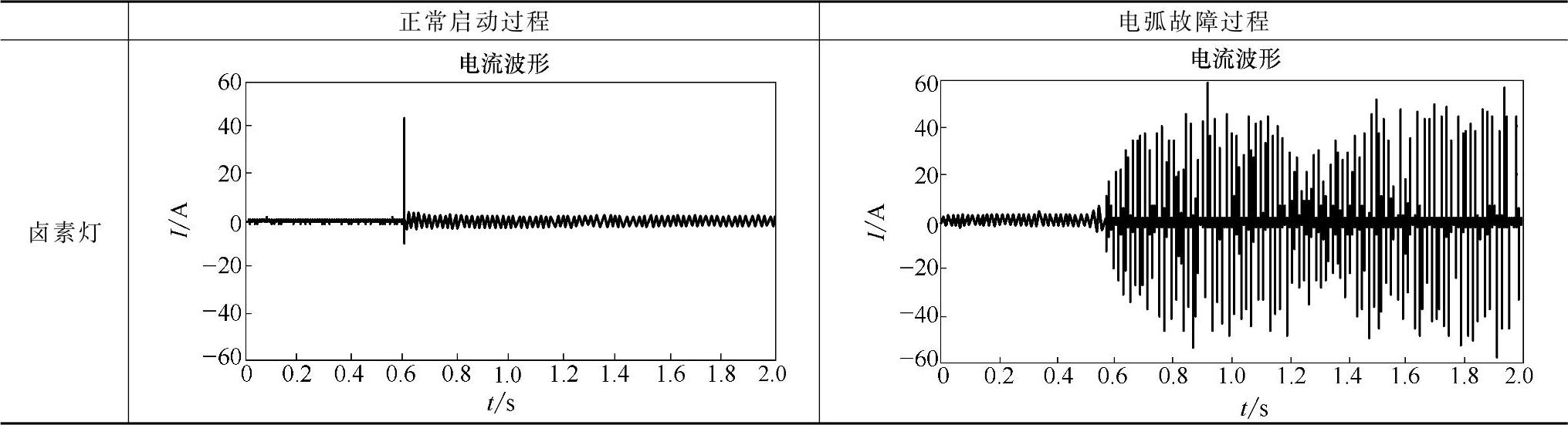
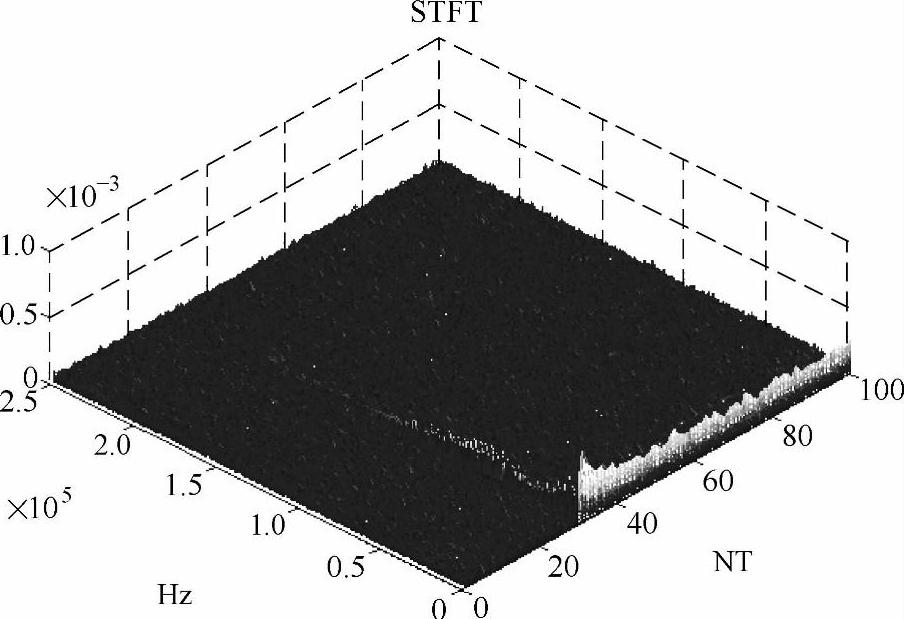
图13-23 卤素灯正常启动过程时频曲线

卤素灯发生串联电弧故障时频曲线以及电弧故障时刻前后平均STFT结果曲线分别如图13-25和图13-26所示。从图13-25可见，电弧故障发生前（第1～27个周期），无明显频率分量变化，发生电弧故障后（第28～100个周期），整个频率范围均存在变化。从图13-26也可见，无明显频率分量变化；发生电弧故障后在500Hz～100kHz范围内变化较为明显，其中5kHz、47kHz、80kHz三处呈显著峰值。

3.空气压缩机电流波形的频谱分析

空气压缩机型号为PUMA XQ235B100F，功率为2200W，起动电流最大峰值为80A。正常起动过程以及电弧故障过程的电流波形见表13-4，在起动过程中，电流波形呈指数衰减，并逐渐趋于稳定；出现电弧故障时，电流波形存在明显变化。

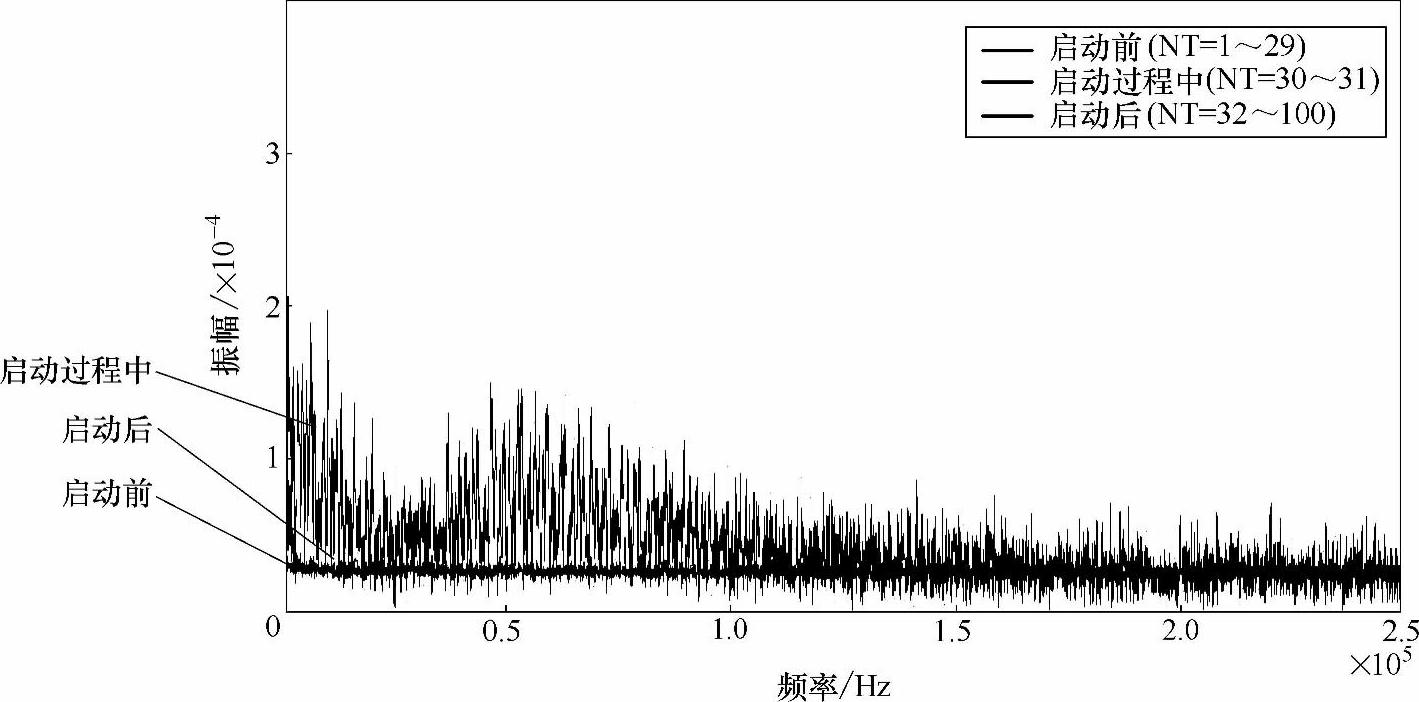
图13-24 卤素灯启动时刻前后平均STFT结果曲线

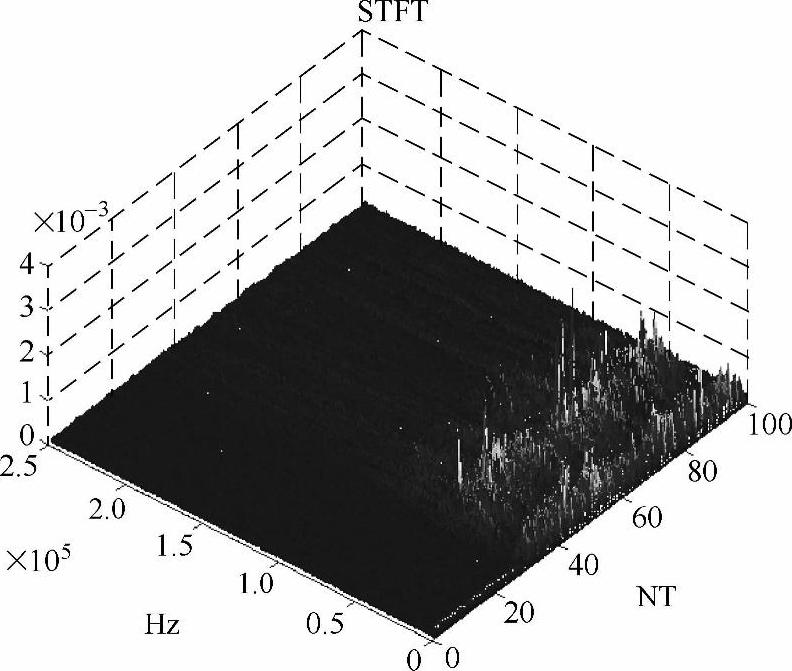
图13-25 卤素灯发生串联电弧故障时频曲线

PUMA空气压缩机正常起动过程中100个周期的STFT时频曲线及起动时刻前后平均STFT结果曲线分别如图13-27和图13-28所示。起动前的第1～48个周期内，无明显变化；在起动过程第49～65个周期内，能量主峰值约为500Hz；在起动过程后的66～100个周期内，频率波动趋于稳定。从图13-28可以看出，起动过程中，频率分量峰值主要集中在457Hz，起动前和起动稳定后无此频率分量；在起动电流波形中存在某些固定频率分量，能量峰值主要位于1.86kHz、156kHz、169kHz、177kHz处。

PUMA空气压缩机串联电弧故障时频曲线图以及电弧故障时刻前后平均STFT结果曲线图分别如图13-29和图13-30（平均STFT仅显示0～3kHz频率范围）所示。从图可见，发生电弧故障时频率变化主要集中在400Hz～2kHz范围内，其中500Hz频率处有明显化。

图13-26 卤素灯电弧故障时刻前后平均STFT结果曲线

表13-4 空气压缩机电流波形

13.2.4.3 频谱分析在电弧故障检测中的应用前景

通过对LED节能灯、电子式荧光灯、电感式荧光灯、紧凑型荧光灯、调光灯（晶闸管型）、卤素灯、计算机、电钻、吸尘器、空气压缩机、电吹风机、空调器等多种负载波形的频谱分析，可以得到的初步结论如下：

1）负载在正常起动过程中，通常会存在瞬时冲击电流，但持续时间不长，如电吹风机、卤素灯等约为2～3个工频周期，某些负载会有较大的起动电流，然后呈包络状逐渐衰减趋于稳定，如空调器电流波形包络衰减至稳定约为7个工频周期。频谱在起动瞬间以后均非常稳定，不存在波动。

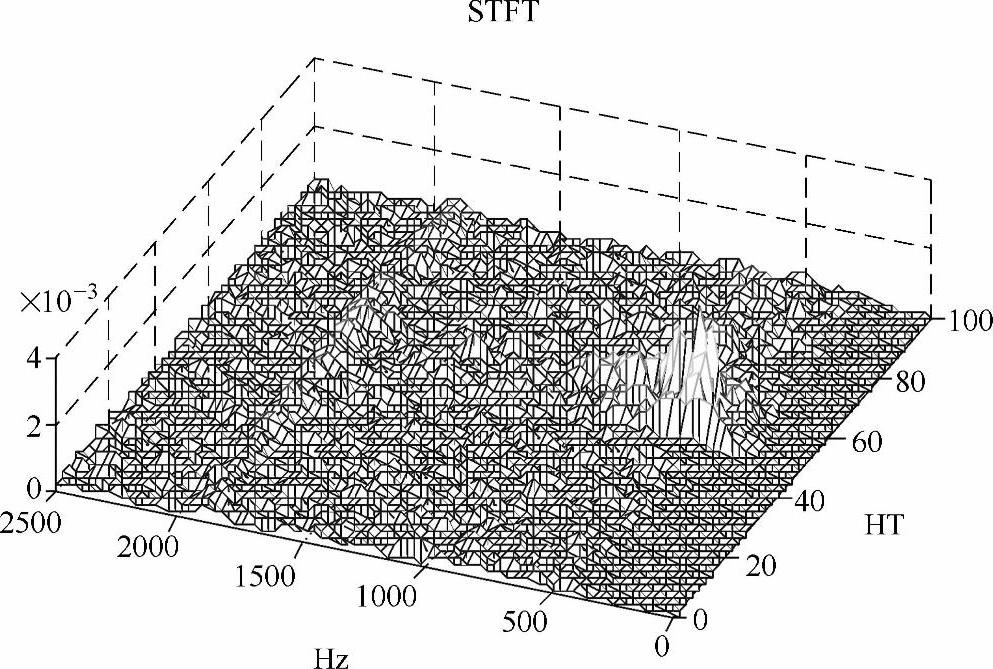
图13-27 PUMA空气压缩机起动过程时频曲线

2）负载在起动后，均会存在一些固定频率分量。这些频率分量分为两类：一类与负载无关、幅值稳定且一直存在；另一类与负载有关，是与负载正常工作的工频电流相对应的频率分量或谐波分量。

3）出现电弧故障时，各种负载在频域内所表现出来的变化特征不尽一致。某些负载在较宽的频段范围内存在显著变化，如电感式荧光灯、卤素灯、电钻等；某些负载只在局部频段范围存在变化，如空气压缩机只在500Hz左右范围内存在不太明显的变化。但所有负载在电弧故障后频谱均有不同程度的波动，增大减小趋势不同，体现出较强的随机性，这与电弧过程中所表现出的能量不稳定状态相吻合。

由于收集样本数量及实验的次数有限，从目前得到的频谱分析数据还不能给出一个较为清晰的、可以作为电弧故障判别依据的结论。但通过上述分析，可以看出不同负载的电弧故障均具有波动变化的共性，这种变化的频率范围较为分散，可考虑选取其中较为集中的一个或几个特征频率段作为信号处理的突破口，进行电弧故障的识别。目前，可将这些特征频率段的波动变化作为电弧故障的辅助判别措施，以提高现有判别方法的可靠性。

图13-28 PUMA空气压缩机起动时刻前后平均STFT结果曲线

图13-29 PUMA空气压缩机串联电弧故障时频曲线

电弧故障波形、正常电弧波形及类似电弧负载种类繁多，运行环境条件复杂多变，使得样本波形收集、频谱分析和数据处理的工作量十分庞大，需要较长的时间才能取得成效。但这是电弧故障检测的一项基础性工作，对提高电弧故障检测的可靠性有很大的意义。下一步应继续开展频谱分析研究工作，广泛收集各种负载电流波形和电弧电流波形（包括正常电弧和电弧故障），采用合理、科学的数据分析和数据处理方法，建立合适的数学模型和电弧故障数据库。通过样本数据的积累，找出电弧故障特征量的变化规律，为高准确度的电弧故障检测技术奠定基础。

图13-30 PUMA空气压缩机电弧故障时刻前后平均STFT结果曲线