交流接触器磁系统静特性仿真优化

接触器的核心部件是电磁机构，电磁机构是感受部件，因而，研究电磁机构是分析接触器的基础。在接触器的设计过程中，对其电磁机构静态特性的分析计算具有重要的意义。电磁机构的静特性通常是指静态吸力特性和反力特性，吸力特性和反力特性之间配合良好是实现电磁机构可靠吸合、提高设备的灵敏度和电气寿命等要求的基本保证。电磁机构良好吸力特性的设计必须基于对电磁机构静态特性的正确分析。

早期的交流接触器电磁机构特性的仿真，主要采用基于磁路的方法进行求解。磁路方法对磁场的分布进行一定的近似等效，导致求解的准确度不高。随着计算机技术和场域仿真技术的发展，采用数值算法计算接触器的磁场，对其静态特性进行分析可以得到较为准确的结果。这里基于三维有限元方法介绍交流接触器静态吸力特性的仿真方法。

电磁铁的静态吸力是指当动铁心位于某一位置，电磁机构达到稳态时对动铁心产生的电磁吸力。因此在计算时，不需要考虑各种过渡状态，吸力值由电磁线圈中电流的稳态值所决定。由电磁场理论可知，电磁铁中的磁场满足方程：

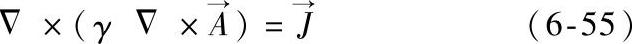
式中 γ——介质的磁阻率；

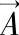——向量磁位；

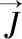——电流密度。

电磁铁静态特性是指在给定线圈电压下，电磁吸力F与工作气隙δ的关系：F=f（δ）。对交流电磁铁来说，若取磁能有效值，则计算的吸力为一个周波的平均值。若忽略铁心的涡流损耗，则线圈电压与电流的关系可用下式表示：

式中 U——线圈外施电压；

E——线圈反电动势；

I——线圈电流；

R——线圈电阻。

用向量图可表示它们之间关系，见图6-51。

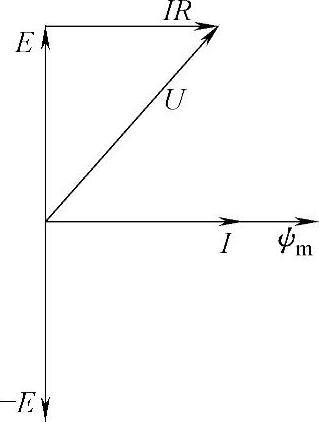
图6-51 向量图

交流电磁铁线圈的感应电动势与磁链的关系为

式中 E——线圈感应电动势有效值（V）；

ω——电源角频率（1/s）；

ψ——线圈磁链的幅值（Wb）。

其中，线圈磁链是线圈电流和气隙的非线性函数，即

ψ=f（i，δ） （6-58）(www.xing528.com)

它可在给定电流和气隙值时，由磁场计算求得。

用有限元法计算电磁铁的静态电磁吸力F时，磁场中的激磁电流密度是作为已知条件给出的。但在交流电磁铁中，稳态时的激磁电流值是随着气隙的长度而变化的，因而必须对不同气隙下的激磁电流值分别加以计算。所以首先必须联立求解非线性方程组式（6-56）和式（6-58），求得在给定气隙和线圈电压下的线圈电流I，再通过有限元分析软件ANSYS计算电磁吸力F。

为了求解非线性方程组式（6-56）和式（6-58），首先假设一初始电流值I₀，由此依次计算出电磁机构的磁场能量、线圈磁链、线圈感应电动势，最终得到线圈端电压。

磁场能量W（幅值）为

其中，磁场强度H以有效值表示，而磁感应强度B以幅值表示。分析中磁能的积分可以通过对所有单元的能量求和获得，即将各个单元的磁感应强度B、磁场强度H和单元体积ΔV列表，然后根据公式（6-60）求得：

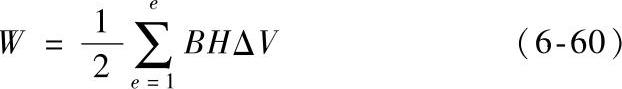
由于磁能又可以由式（6-61）表示：

因此磁链为

故感应电动势为

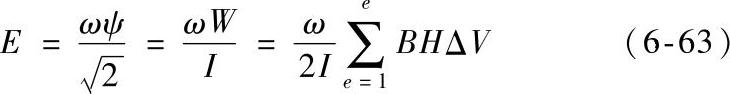
计算出感应电动势E后，就可以根据公式（6-56）计算而得到相应的端电压U，将计算得到的端电压U与实际给定的线圈电压U_e相比较，如不能满足准确度要求，则校正电流值为

重复以上的计算，直至准确度达到要求。该方法充分利用了ANSYS软件的寻优功能来实现线圈电流的求解，以线圈电压的计算结果U和给定电压U_e的差值U_opt达最小为寻优目标，把线圈电流值I₀设定为自变量作为设计变量，计算结果I₁与初始设定值之差I_opt作为状态变量。反复迭代，直至满足各优化变量的约束条件并使目标函数达到最小，则获得的电流值I₁即为给定气隙和线圈电压下线圈中的电流，将得到的电流加载在线圈单元上，即可进行静态吸力特性的计算。

对于直流电磁铁，线圈中的励磁电流由线圈两端的电压和线圈电阻决定，因此线圈电流是已知的，可以直接利用有限元分析软件ANSYS计算不同气隙下的电磁吸力F。

应用上述方法对某一型号额定电流为80A的交流接触器电磁机构静态特性进行仿真，计算所得接触器的吸力特性与反力特性配合曲线如图6-52所示。

图6-52 吸力特性与反力特性配合曲线

1—反力特性曲线 2—吸合电压下吸力特性曲线 3—额定电压下吸力特性曲线

为了验证计算方法的正确性，通过实验测定此交流接触器在线圈额定电压220V下不同气隙时的吸力和电流，实验结果与仿真结果对比如图6-53所示，由图可见这种计算交流电磁铁电磁机构静态特性的方法是可行的。