低压电器温度场仿真及温升计算优化

国际标准和国家标准对低压电器各部分的极限允许温升有明确的规定。制定电器各部分极限允许温升的依据是：保证电器的绝缘不会因温度过高而损坏，或使工作寿命过分降低；导体和结构部分不至于因温度过高而降低其机械性能。低压电器的温度场仿真与温升计算的目的在于研究电器在工作状态下的发热，保证各部分最高温度不超过规定的极限允许温度，以保证其工作的可靠性。此外，发热计算在电器设计中对于缩小体积、减轻重量、节约原材料等方面也都有重要意义。

低压电器各部分的发热与散热是一个非常复杂的过程，影响它的因素很多，很难建立一个考虑到所有影响因素的热过程解析公式。随着计算机技术及场域仿真技术的发展，采用数值算法计算电器的温度场，可以得到较为准确的结果。下面主要介绍如何应用三维有限元软件ANSYS进行接触器温度场的仿真分析。

低压电器中的热传递有传导、对流和辐射三种形式。电器产生的热损耗通过这三种形式散失到周围介质中去。

热传导遵循傅里叶定律：

q=-λgradθ （6-49）

式中 q——热流密度；

λ——热导率。

热对流仅在流体中存在，可以用牛顿冷却方程来描述：

q=h（θ-θ₀）

式中 q——热流密度；

h——对流散热系数；

θ——发热体表面温度；

θ₀——流体介质的温度。

根据斯蒂芬—波尔兹曼定律，物体单位面积的辐射功率如下所示：

q=σε_f（T⁴₂-T⁴₁） （6-50）

式中 q——热流密度；

ε_f——辐射率；

σ——斯蒂芬—波尔兹曼常数，σ=5.67×10^-8W/（m²·K⁴）；

T₂、T₁——发热体和接受辐射物体表面温度。

国家标准规定，低压电器零部件的极限允许温度只有百度数量级。当绝对温度为T₂，表面积为S的电器零部件处在空间范围较大，温度为T₁的空气中，其辐射热阻可以用下式表示：

式中 S——电器零部件的表面积，（m²）。

由上式（6-51）可以看出，电器零部件的辐射热阻数值很大。而它们极限允许温度只有百度数量级，辐射功率较小，故电器的散热方式主要考虑对流和传导。

由于交流接触器的温升按国家标准和IEC标准规定，应同时考虑主回路和操作电磁铁的发热，因而这里取接触器作为对象来分析其温度场分布和介绍温升计算。主回路发热包括电流流过回路导体时的损耗、动静触头接触电阻的损耗以及连接导线和接线端的损耗；直流电磁系统发热主要是线圈发热，而交流电磁系统发热包括线圈和分磁环的损耗以及铁磁体的涡流和磁滞损耗。由于热量主要是由于电流通过导体产生的，因此在应用有限元方法对接触器温度场进行分析是基于热电耦合进行的。通过接触器温度场数值分析可以更加精确地设计各个零部件和导体回路，减少不必要的贵金属的用量，节约材料；同时可以大大缩短测试时间和开发周期，提高设计效率。

为了说明接触器的温度场仿真计算，取一额定电流为100A的交流接触器作为研究对象，图6-47所示为交流接触器的结构图，在进行有限元分析计算时充分利用其对称性，取四分之一模型建模。

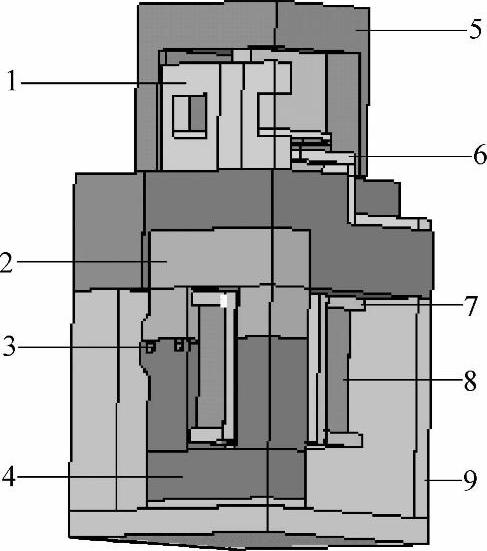
图6-47 交流接触器模型

1—动触头支架 2—动铁心 3—分磁环 4—静铁心 5—顶盖 6—主回路 7—线圈骨架 8—线圈 9—外壳

交流接触器长期闭合工作时产生的热损耗通过传导、对流和辐射散失到周围介质中去。由于接触器内部空气对流缓慢，在进行热分析时只考虑接触器内部传导散热，忽略对流和辐射的影响。对其外壳和连接导线考虑对流和辐射散热，通过表面散热系数来简化处理其散热。

建立热分析模型的基本假设：

1）接触器处于无限大空间；(www.xing528.com)

2）由于结构的对称性，认为对称面是绝热面；

3）材料各向同性；

4）外表面的对流散热为自然对流散热；

5）环境温度不变，为实验时测得的室温。

在以上假设条件下，稳态时交流接触器内部三维热传导方程为

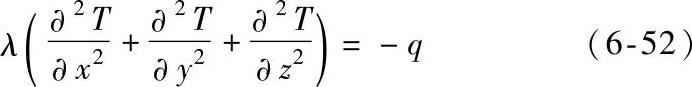
式中 T——物体的温度；

λ——导热系数；

q——单位体积内热源的生成热。

边界条件：

（1）对称面为绝热边界条件为

（2）交流接触器外壳外表面、主回路静触头导电回路外壳外部分、接线端外表面为散热边界条件为

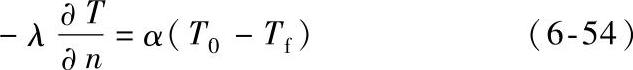
式中 α——表面散热系数；

T₀——发热体温度；

T_f——环境温度。

式（6-52），式（6-53），式（6-54）即为交流接触器稳态温度场的求解问题，通过求解可以得到其温度场分布。

应用三维有限元分析软件包ANSYS对图6-47所示的交流接触器进行了温度场仿真，接触器内部的温度分布如图6-48所示，图中标识的10、11两点为实验测试温度的点。

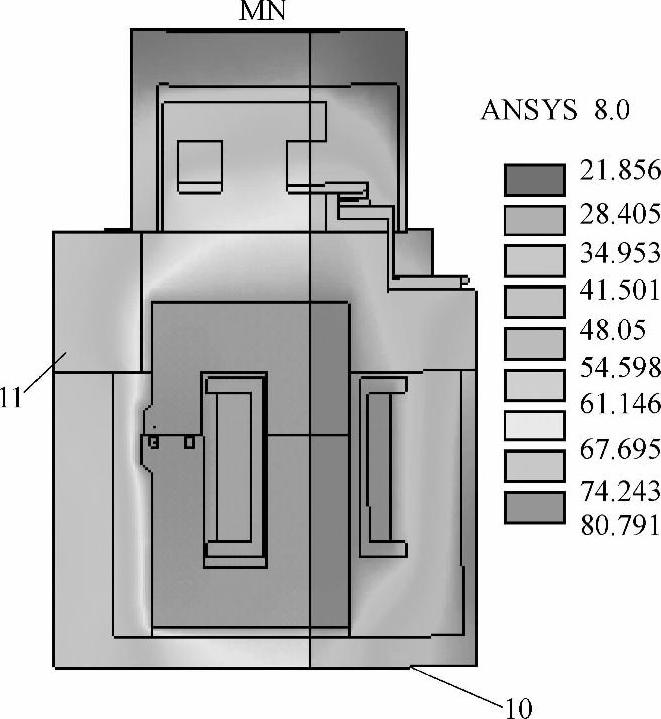
图6-48 接触器内部温度场

10、11—实验测试温度的点

由图6-48可知接触器主回路部分的温度低于电磁铁部分。主回路和电磁铁部分的温度分布如图6-49所示，图中标识的1～9为实验测试温度的点。

由图6-49a可见，由于分磁环的发热，动静铁心在分磁环附近温度较其他位置高，但铁心总的温差不大，温度分布比较均匀。由图6-49b可见，对于主回路的每一相，由于接触电阻的存在，触头接触处温度较导体其他部分高。主回路三相比较，中间相的温度比旁边相高，这主要是由于中间相的两边都存在旁边相，而旁边相有一边是外壳，散热比中间相容易。

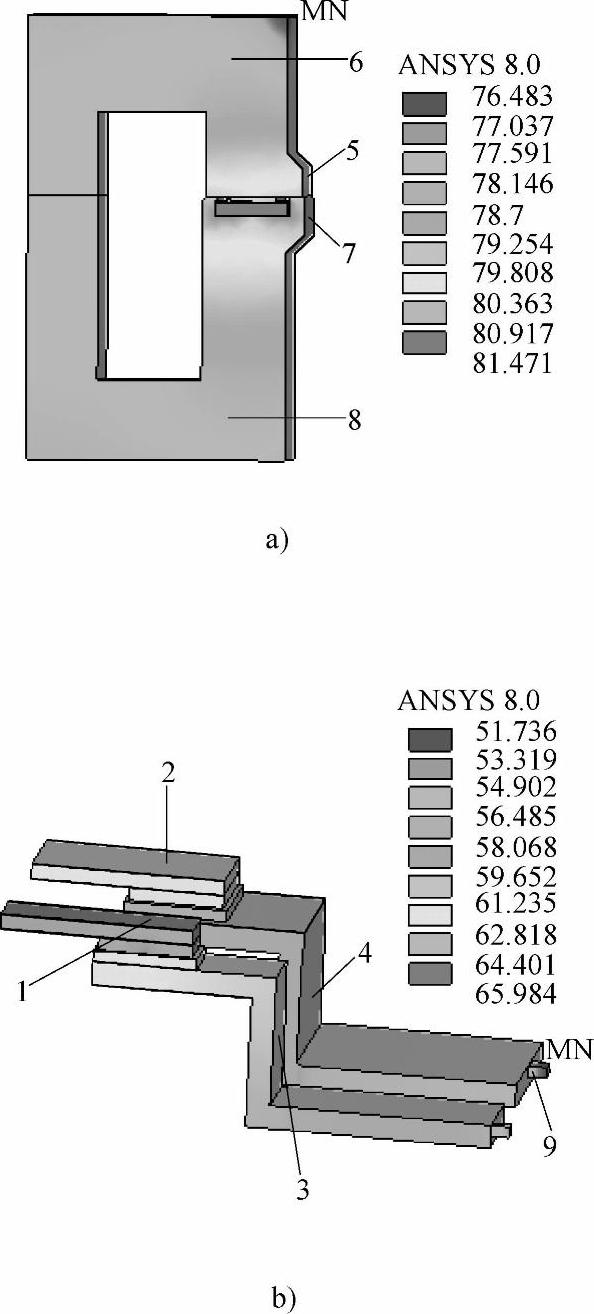
图6-49 接触器电磁铁和主回路部分温度

1～9—实验测试温度的点

a）电磁铁 b）主回路

为了验证计算方法的正确性，根据国家标准，给主回路和线圈同时通电进行实验，用长1m截面积为35mm²的导线将主回路三相串联，采用电流调压器给主回路通100A电流，在线圈两端加220V额定电压，达到稳定温升后，用电阻法测量了线圈的平均温升，用热电偶测量了动静铁心以及动静触头上选定点的温度。

计算值和实测值比较如图6-50所示，其中1～9所表示的点如图6-49标识的点1～9所示。点10、11如图6-48标识分别位于外壳底面和侧面。计算值与实验值之间存在误差，尤其是主回路温升计算值要低于实测值，误差最大为8.4%，这主要由于动静触头接触电阻和接线端接触电阻是主回路的主要热源，而在计算接触电阻时假设接触处只有收缩电阻，因此接触电阻计算值要小于实测值；同时模型的一些简化以及材料导热系数的选择也会产生误差。