塑壳断路器电动斥力计算及应用探析

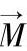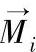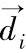对于MCCB来说，动触头是在一个对转动轴的力矩的作用下打开的，如图6-30所示。作用在其上的等效电动力可以通过式（6-43）求得。也就是说，对任何一个单元i来说，其对于转轴O的转矩为和力密度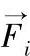的向量积，那么在整个动导电杆区域对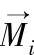进行体积分运算，则可得到作用在其上相对于O的力矩，力矩除以力臂l就可以得到等效电动力。

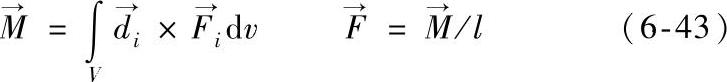
图6-30 作用在动导电杆上的电动斥力计算示意图

采用三维有限元分析，可以得到作用在动导电杆上和触头上的电动斥力。由于该力和短路电流之间存在单调增的关系，不考虑铁磁物质的影响时，电动斥力与短路电流的二次方成正比。而且在特定的短路条件下，短路电流和时间有一定的关系，若在触头斥开之前，取电路方程为式（6-44），其中I为电流第一半波的有效值，频率为工频50Hz。这样就可以完成对上述过程的迭代处理，当电动斥力F等于触头预压力F_K时，迭代结束，此时对应的时间即为触头斥开的时间。图6-31为计算触头斥开时间的迭代流程图。为了考虑电流对触头压力和相应的导电桥半径的影响，电动斥力、触头压力和导电桥半径每隔100A计算一次。

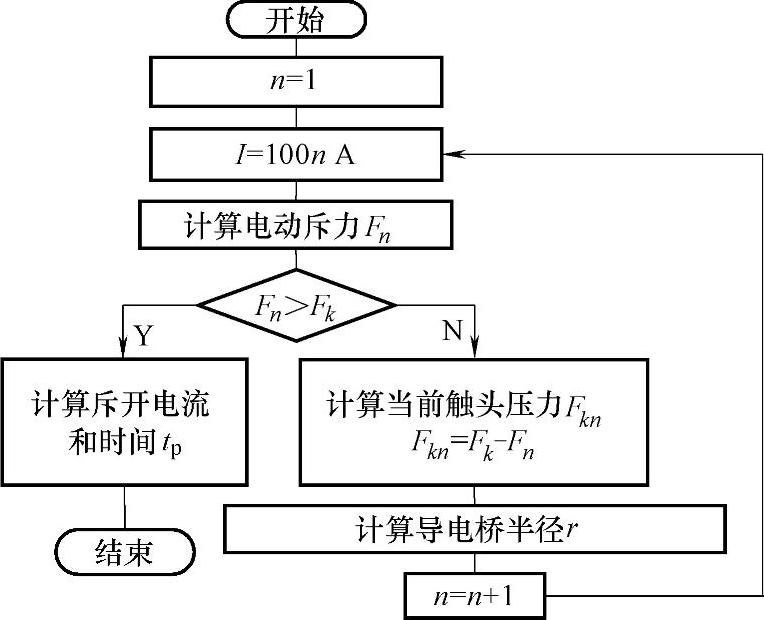
图6-31 触头斥开时间计算流程图

1.触头间电接触的导电桥模型

一般来说，看似平坦光滑的触头表面其实是凹凸不平的，而且覆盖有一层不导电的氧化层。不同的触头材料、不同的加工方法、不同的工艺过程所得到的表面微观状态都不相同，它将在很大程度上影响两金属表面相互接触的物理过程和接触表面的物理图景。而在触头压力弹簧的作用下，触头表面将发生塑性变形，绝缘膜破裂后形成分布的微小导电斑点。

这样，当电流流过触头，电流线在接触面附近发生收缩，因而在触头间会产生电动斥力，也即霍姆力F_H。一般来说，它与电流瞬时值i，触头间的预压力F_K，触头材料的布氏硬度H，触头形状及触头表面的导电斑点分布情况等有关。可以用式（6-45）所示的霍姆公式来描述。其中r为导电斑点的半径，R为触头的等效半径，ξ用来表征触头的表面接触情况，其范围为0.3～0.6，一般取0.45。

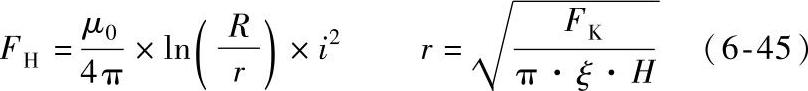
对于霍姆公式的一般工程应用来说，假定接触面中心只有一个导电斑点，或者认为全部的导电斑点集中在中心形成一个大的导电斑点。

在进行电动斥力的数值计算时，可以采用导电桥模型来模拟触头间的电流收缩，图6-32为导电桥模型的示意图。导电桥材料属性和触头相同，接触半径r可用式（6-45）得到，高度h可取0.2mm。

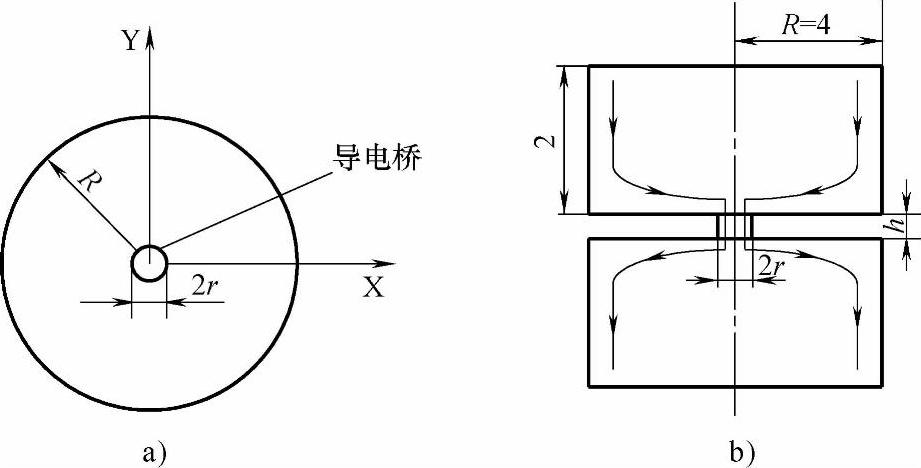
图6-32 导电桥模型示意图

a）正视图 b）前视图

2.几种不同结构的MCCB电动斥力分析

本节应用上述方法，采用三维有限元非线性分析，首先针对5种MCCB，对比分析了触头灭弧系统结构对触头闭合时电动斥力的影响；并计算了触头的斥开时间。

对两种额定电流均为100A的塑壳断路器产品CB1、CB2进行了仿真。其中CB1静导电杆采用水平面U型，而CB2采用下进线U型，分别如图6-33a、b所示。为了研究不同的触头灭弧系统对电动斥力的影响，在不改变产品其他形状及尺寸下，将CB1的静导电杆改为平板式，形成如图6-33c所示的CB3模型；将CB2的栅片腿长缩短，并加入U型电机槽，形成如图6-33d所示的CB4模型；去掉CB1模型的灭弧栅片，形成CB5模型。图6-33a和6-33c的右下角分别为CB1和CB3静触头区域的俯视图和电流方向的示意图。(www.xing528.com)

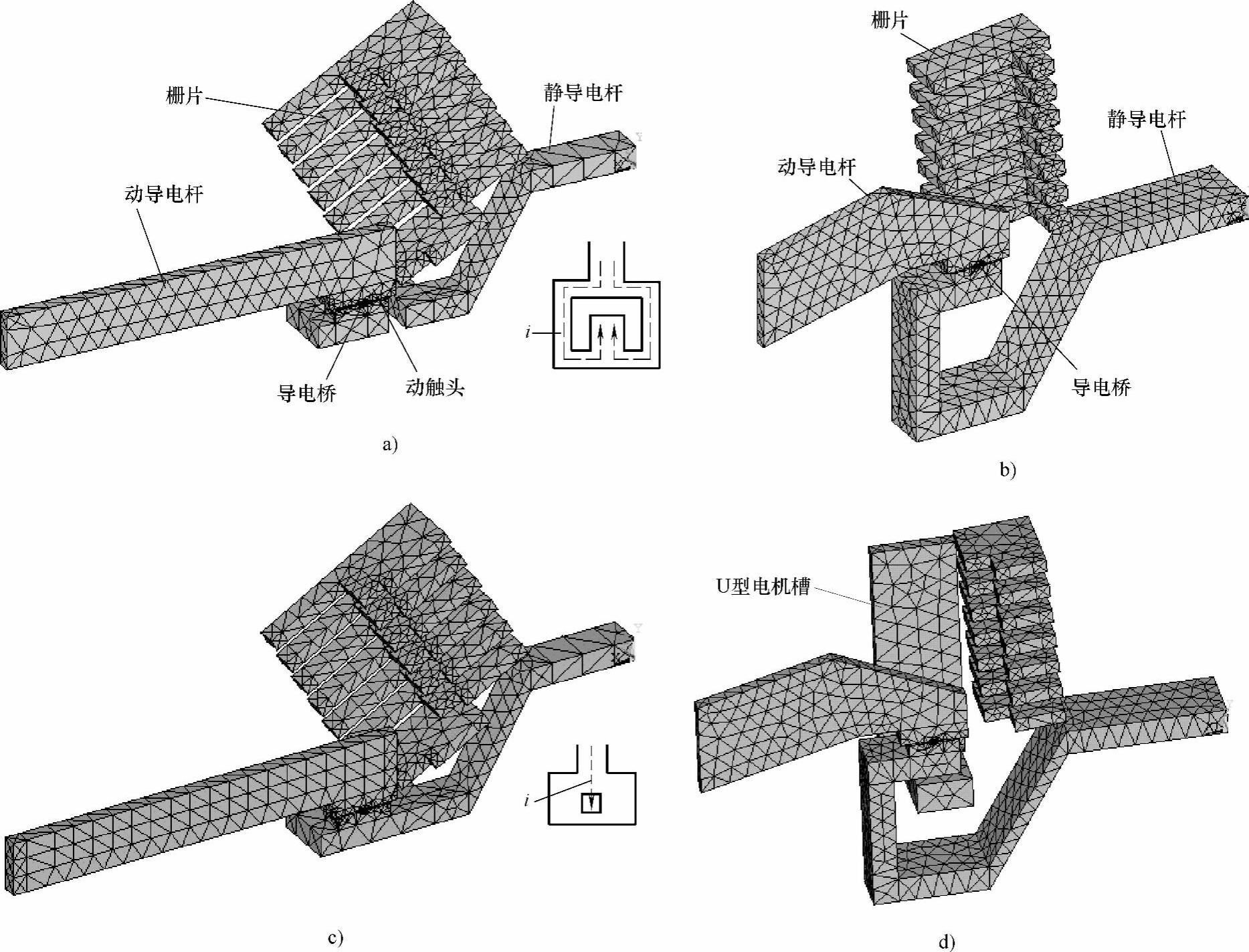
图6-33 MCCB模型的剖分图

a）CB1 b）CB2 c）CB3 d）CB4

同样地，由于各个模型均关于中心面对称，这样仅需要一半建模与计算。对应于图6-33a右下角的电流方向，和图6-34b不同，从图6-34a所示的CB1俯视图可以清晰地看到由于其静导电回路的U型弯曲导致图6-34中1所示部分的电流方向和动导电杆相反。另外，本节所有分析都是相对于图6-34a所示的坐标系进行的，其中X、Y及Z轴正方向符合右手法则，在图6-34中，Y轴正方向垂直纸面向外。从图6-34c可以看出，触头上由于电流收缩，其电流密度最大值比动导杆上高5个数量级。

图6-35a、b分别为沿CB1和CB3动导电杆上Z方向的平均磁感应强度B_Z和Y方向上的平均力密度f_Y分布，其原点为动导电杆的左端，也就是图6-30中的A点。可以发现，靠近触头的区域，磁场和力密度均比较大，而且该区域远离转轴，力臂较大，因而可以认为，回路电动斥力，也就是洛伦兹力F_L主要取决于这部分。同时明显看到CB1的磁场和力密度较CB3大。

在统一计算霍姆力F_H和洛伦兹力F_L的数值分析过程中，也可以认为作用在动导电杆上B点（见图6-33）的等效合力由两部分组成，即认为作用在动导电杆上的力为F_L，作用在动触头上的力为F_H，这一点可以通过下面的仿真来验证。对CB2，10kA电流时，不考虑触头间的电流收缩时，作用在动导电杆和动触头上的合力为15.66N；另一方面，考虑触头间的电流收缩时，作用在动导电杆上力为12.34N，而作用在动触头上的力为30.98N。因此，为了便于接下来的分析，分别用F_L和F_H来近似描述作用在动导电杆和动触头上的电动斥力。

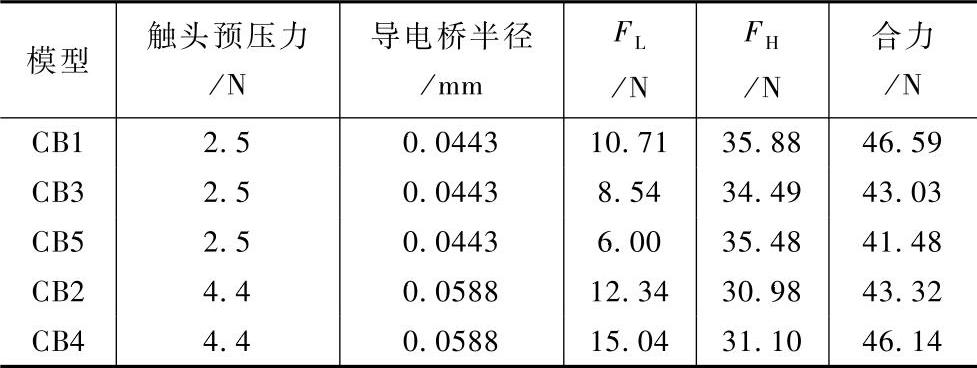
从表6-13所示的对CB1的计算数据来看，电动斥力和电流的二次方近似成正比例关系。表6-14所示为10kA电流时，五种模型的电动斥力计算结果。从表6-13和表6-14中可以看出，F_H占整个电动斥力的70%左右。比较CB3和CB1的计算结果，将静导电杆的形状从水平U型改为平板型，电动斥力有所减小，说明水平U型通过改变电流的方向，有利于加强触头区域的磁场及相应的电动斥力，这一点也和图6-38的结果相一致。对CB5来说，由于没有栅片，和CB1相比，F_L的数值减小了40%左右，说明铁磁物质可以有效地加强动导电杆上的磁场。对CB4来说，通过改变CB2的栅片尺寸并加入U型电机槽后，电动斥力也有所增大。同时，这种改进也有利于将产气材料固定在电机槽内侧，利用新的气吹灭弧原理提高MCCB的开断性能。

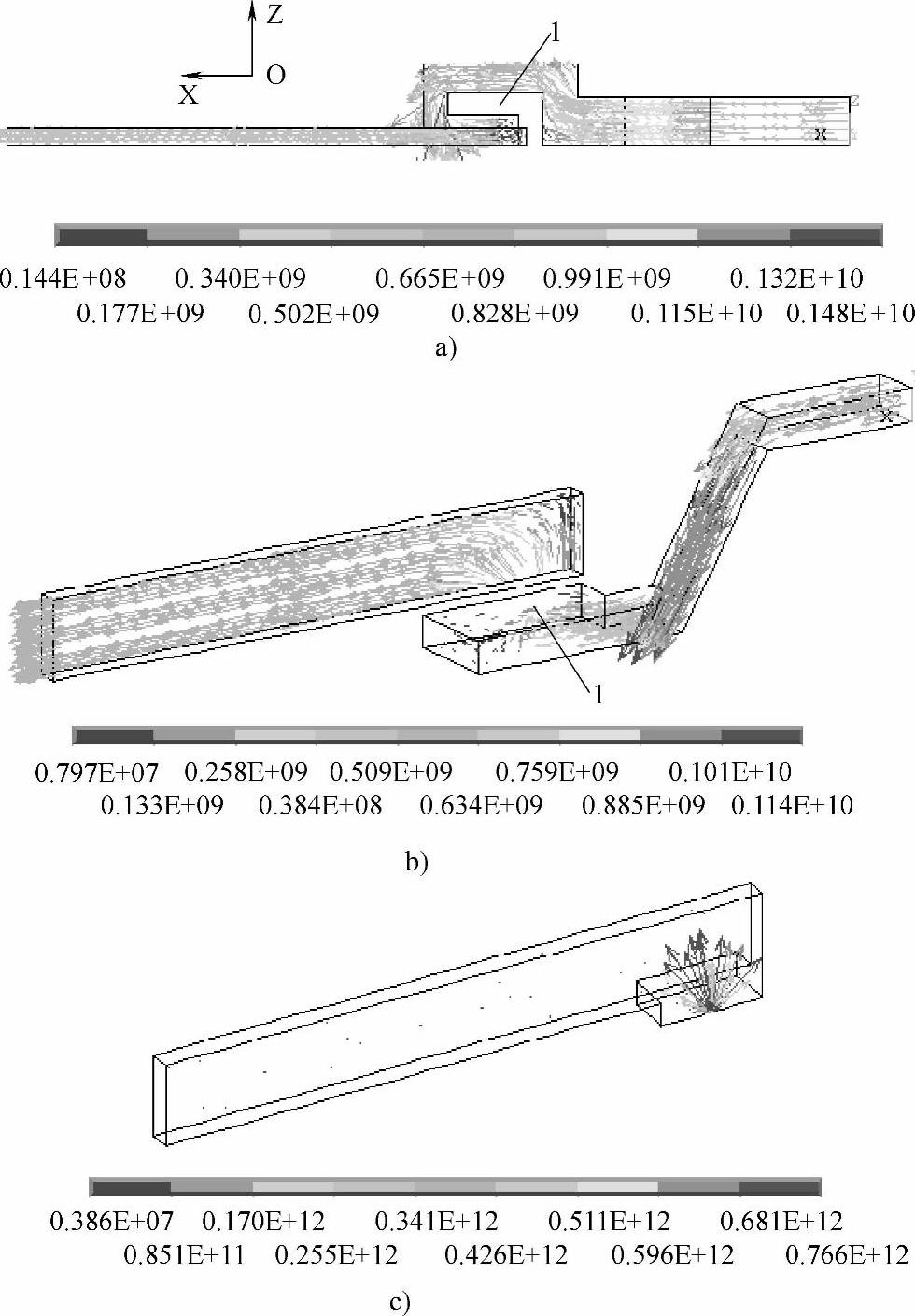
图6-34 模型电流密度分布

a）CB1动、静导电杆电流密度分布 b）CB3动、静导电杆电流密度分布 c）CB1动导电杆和动触头电流密度分布

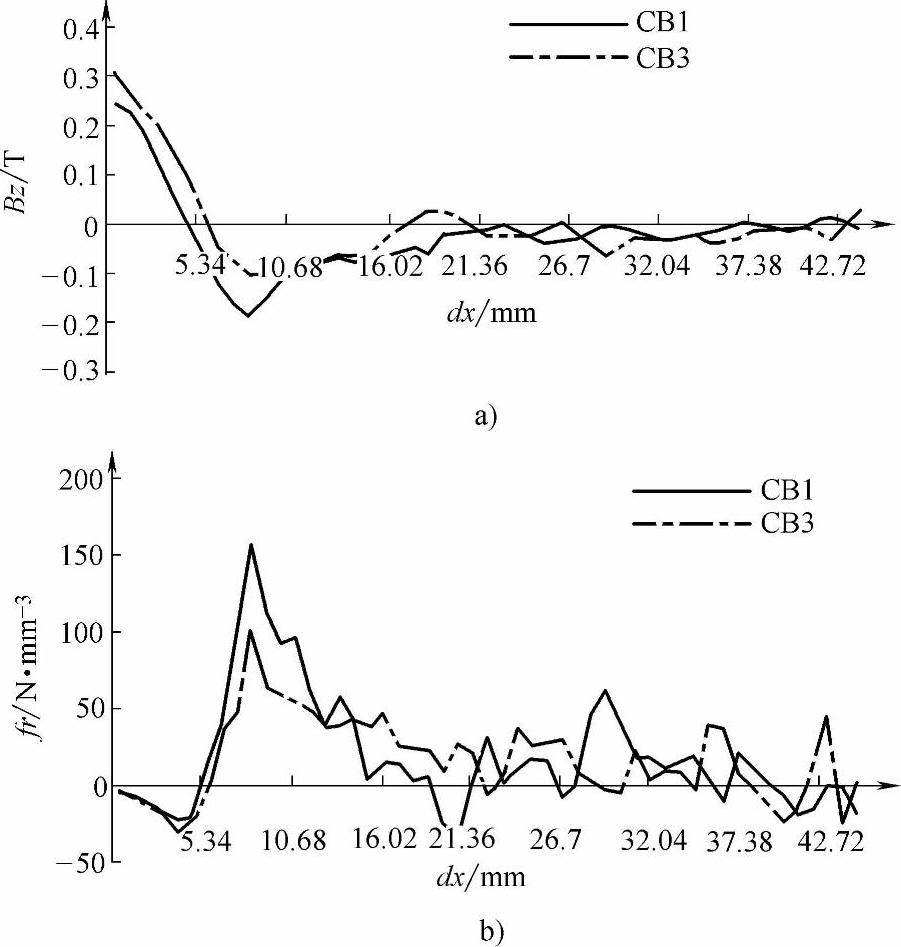
图6-35 CB1和CB3动导电杆上的磁感应强度和力密度分布

a）动导电杆上沿Z向磁感应强度分布 b）动导电杆上Y方向上力密度分布

此外，在表6-14所示条件下，可以用霍姆公式来计算作用在动触头上的电动斥力F_H。对CB1和CB2来说，F_H分别为40.33N和38.45N，同表6-14的结果相比，有一定的差别，这主要是由于导电回路产生的磁场对动触头上电动斥力的影响引起的。

此外，如果忽略触头压力和导电斑点半径之间的关系，并假定电动斥力和电流的二次方成比例关系，就可以初步设计出比较理想的触头预压力。一般来说，断路器瞬时脱扣器的动作电流为额定电流的12倍，由此因电动斥力而使动触头斥开的电流应大于瞬时脱扣器的整定电流，否则机构没有动作而触头斥开，会造成动触头斥开后跌落而与静触头熔焊。对CB2来说，通过计算当触头预压力为4.4N时开始斥开的电流为2825A，因此预压力的设计值应大于下式计算值：（12×2^0.5×100）2×4.4/2825²=1.59N。在此基础上，考虑到脱扣器的安全裕量以及热动稳定性，就可以设计出一个比较优化的触头预压力数值。

表6-13 CB1模型的电流和电动斥力之间的关系

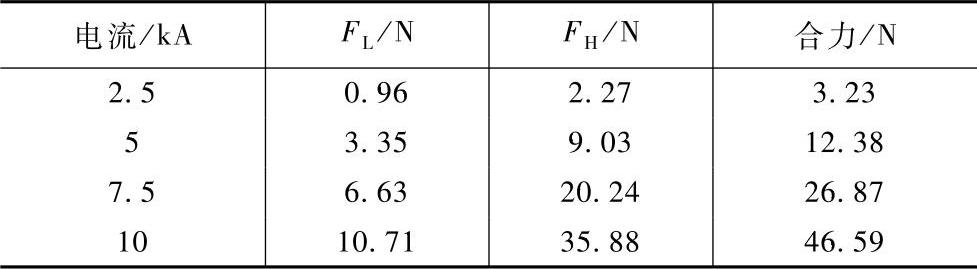
表6-14 五个模型在10kA电流时的电动斥力计算结果