电动斥力数值分析方法

电动斥力的大小决定了断路器工作过程中的电动稳定性、热动稳定性以及断路器的开断性能，因此，在断路器优化设计中电动斥力的计算与分析是一项很重要也很必要的内容。

断路器在工作时，作用在动触头上的电动斥力包括两个部分：由于电流线收缩引起的霍姆力F_H和由于导电回路引起的洛伦兹力F_L。对F_H的研究，主要是如何描述触头间的电接触情况；同时，伴随着电磁场数值计算理论及相关技术的发展，对复杂电气结构下的电动斥力进行较为精确的分析也成为可能。目前，积分方程法和有限元法是断路器中的电动斥力分析的常用方法。

对于电器中电动斥力的计算，关键是求解流过导体的电流密度和载流导体上的的磁感应强度，然后采用式（6-33）就可以求得磁场对载流导体的电动力。其中V为载流导体的体积。

1.积分方程法

设在磁场中的有一场点P（x，y，z），则P点的磁场强度可认为是由两种场源引起的，一是空间电流的作用产生的磁场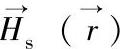，它由电流的大小、分布和场点位置决定；二是磁化后的铁磁物质产生的磁场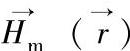，它的大小决定于铁磁物质与场点P的相对位置和铁磁物质的磁化强度，于是空间任一场点P处的磁场强度可表示为

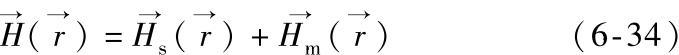
电流的三维分布一般都具有比较复杂的几何形状，难以找到统一的积分表达方式，所以对于的求解通常是将不规则的三维结构剖分成几种基本电流单元，如楔形块、部分螺旋管块和长方体块等。空间中任一点的场值看成是这些基本块所产生场的叠加。同时，对电流源区采用分区剖分的方法，使得每一个分区具有常值电流密度分布。

电流与铁磁物质之间、铁磁物质相互之间形成一个十分复杂的非线性关系。电流流过导体在空间产生磁场，电流磁场引起场区内的铁磁物质磁化，而铁磁物质的磁化又在空间各场点叠加新的场强，这个场强不仅影响到场区其他的铁磁物质，同时也影响到本身。而积分方程法求解磁场问题的基本思想就是认为空间中的任何一点的磁场是由电流源磁场和介质被磁化所产生的磁场的叠加。

对图6-28所示的存在电流源和铁磁物质的空间源区来说，式（6-35）所示的毕奥-萨伐定律可以描述由于源点r1处电流的存在，在空间某点r₂处所产生的磁场强度与电流的大小、方向和分布之间的关系。通过对电流源区进行积分，可求得场区任一点的值。而式（6-36）所示的积分方程可以描述铁磁物质由于磁化所产生的磁场。

在求解式（6-36）时，需要将铁区剖分为许多小块铁单元，每一块单元的物质参数和磁化强度可取不同的数值，但在每一个单元内部物质参数和磁化强度都被看成是一个常量。这样，一个参数连续变化的铁区就被一个离散了的并具有不同物质参数的许多小铁块单元代替。这种剖分的概念和有限元法是类似的。从式（6-36）中可以看出，由于离散，被积函数中的磁化强度矢量在单元中已成常量，故可以提到积分号之外，剩下的被积函数表达式中只与铁单元的几何尺寸及铁单元与场点之间的距离有关。这样，就由式（6-37）成立，同时，磁化强度M可以通过磁化率χ与磁场强度H的乘积来表示，如式（6-38）所示。这样，对与图6-28所示的场区可得到式（6-39）所示的联立方程，其中C_aa、C_ab、C_ba、C_bb均是仅于场域中各部分几何尺寸和相互位置有关的耦合系数。

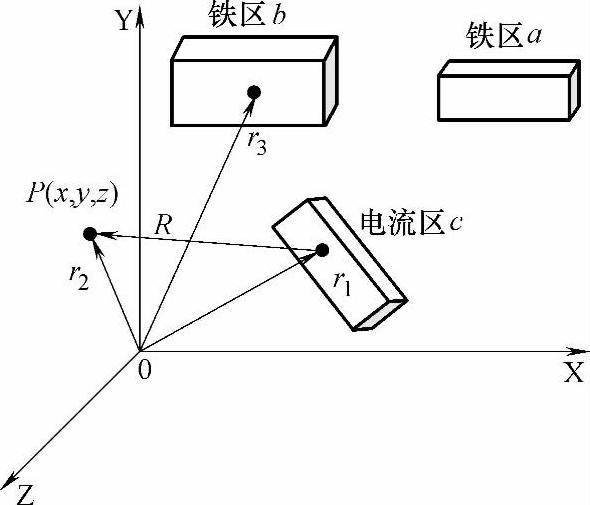
图6-28 空间源区分布

图6-29为利用积分方程法编写程序的基本框图。首先假定一个磁化率χ₀，按不同的几何形状和尺寸进行计算，形成系数矩阵，并计算电流所产生的场量构成方程右端项。然后求解大型联立方程组，方程的解就是磁场强度在各方向上的分量。由此查磁化曲线，得到新的磁化率χ₁，检查χ₁和χ₀之间的误差是否小于给定的误差。如已满足准确度要求，则输出计算结果；若不满足，则将χ₁代回至系数形成部分。这个过程反复迭代进行，直到达到所要求的准确度为止。(www.xing528.com)

图6-29 积分方程法的程序框图

2.有限元法

根据静态电磁场的分析，在导电体区域，也就是触头导电回路，电流密度J满足式（6-40）和式（6-41）所示的公式。

式中 σ——导体的电导率，

——电场强度，

V——标量电动势，

——电流密度矢量。

在得到了电流密度的分布后，在整个场域中，根据磁通密度和之间的关系式（6-42），其中为矢量磁位，μ为磁导率，即可得到的分布。