电磁脱扣器的保护特性仿真分析

1.拍合式电磁脱扣器

塑壳断路器用电磁脱扣器的磁系统一般拍合式占多数，个别额定电流小的也有用螺管式，这里取常用的如图6-3所示的拍合式电磁脱扣器为研究对象，脱扣器额定电流为100A，这种脱扣器依靠连接母排通过的电流作为励磁，以反映主回路电流的大小。图6-3所示塑壳断路器磁脱扣器电磁铁，由于结构上对称，仅绘出其1/2对称模型，图中XOY面为对称面。

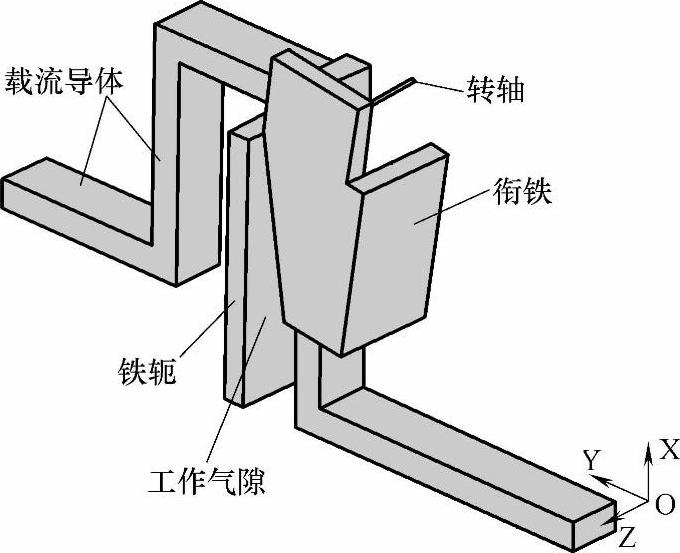
图6-3 塑壳断路器磁脱扣器电磁铁（1/2对称模型）

该脱扣器的电磁铁为拍合式，无铁心，当作为载流导体的母排通过主回路电流达整定值时，由衔铁与轭铁之间的两处工作气隙的磁通产生电磁吸力，克服反作用力，使衔铁动作。

2.脱扣器静态特性计算

磁脱扣器的静态场分析采用三维有限元方法，借助有限元分析软件ANSYS进行，包括载流导体内的电流场分析和脱扣器的磁场分析。载流导体的电流密度分布根据以下两个基本方程进行计算：

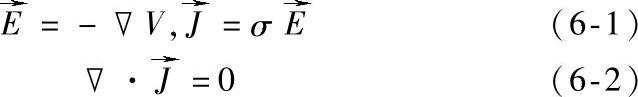
式中 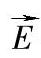——电场强度；

V——标量电动势；

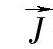——电流密度矢量；

σ——电导率。

式（6-2）为电流的无散度条件，即场域中任意封闭面的净电流为零。

计算得到了载流导体的电流密度分布之后，由其产生的脱扣器磁场根据式（6-3）进行计算。

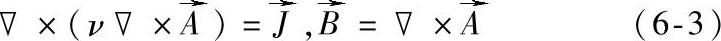
式中 ——矢量磁动势；

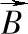——磁感应强度；

ν——磁阻率。

脱扣器的三维磁场计算完毕后，与载流导体匝链的磁链ψ采用式（6-4）进行计算。

式中 n——载流导体匝数；

W——磁场能量；

I——载流导体电流。

衔铁所受电磁吸力采用麦克斯韦应力张量法进行计算：与衔铁接触的空气单元i的应力为T_i，接触面积为s，单元的力密度为F_i，单元质心到衔铁转轴的距离为d_i，则衔铁对转轴的磁转矩M见式（6-5）和（6-6）。

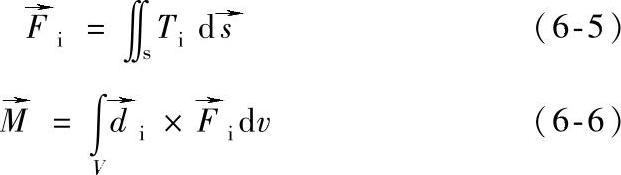
通过上面的方法，就可以计算出磁脱扣器衔铁的磁转矩和磁链随气隙和电流变化的静态数据网格，并用于后面的脱扣器动态特性计算。

图6-4示出了该脱扣器载流导体的电流密度分布（1/2对称模型）。

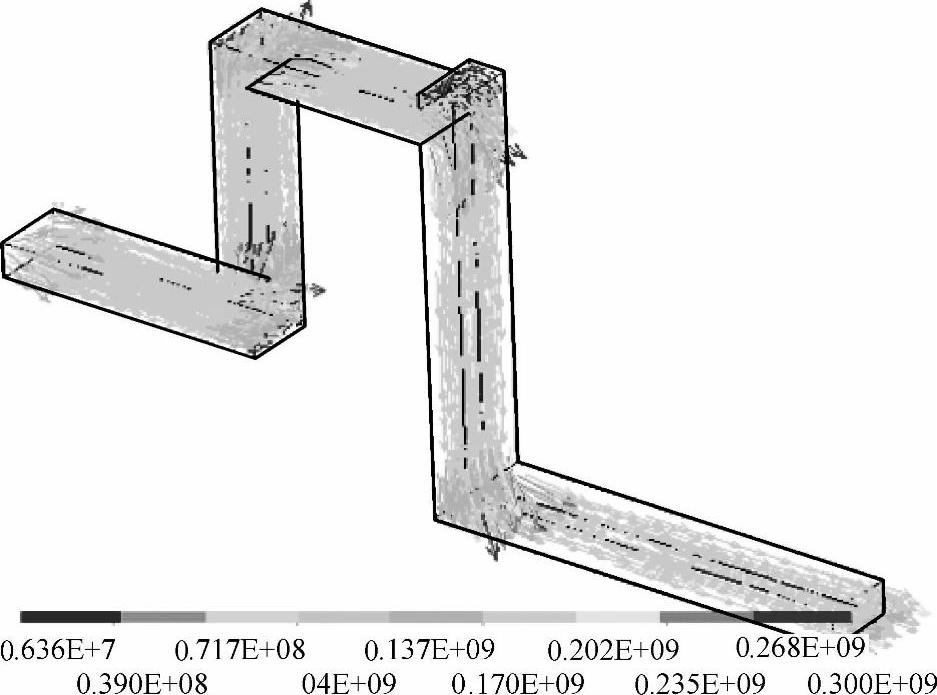
图6-4 磁脱扣器载流导体电流密度分布

在有限元分析中，模型的剖分对计算结果的准确度有至关重要的影响，若剖分不合理，往往会造成很大的误差，误差甚至可达20%以上。为了保证脱扣器三维磁场的计算准确度，采用逐次加密剖分的方法，比较前后两次的计算结果（磁力和磁通），直到相差小于1%为止，这时认为磁场计算误差也低于1%。如图6-5所示为最终确定的磁脱扣器场域剖分（面对对称面）。

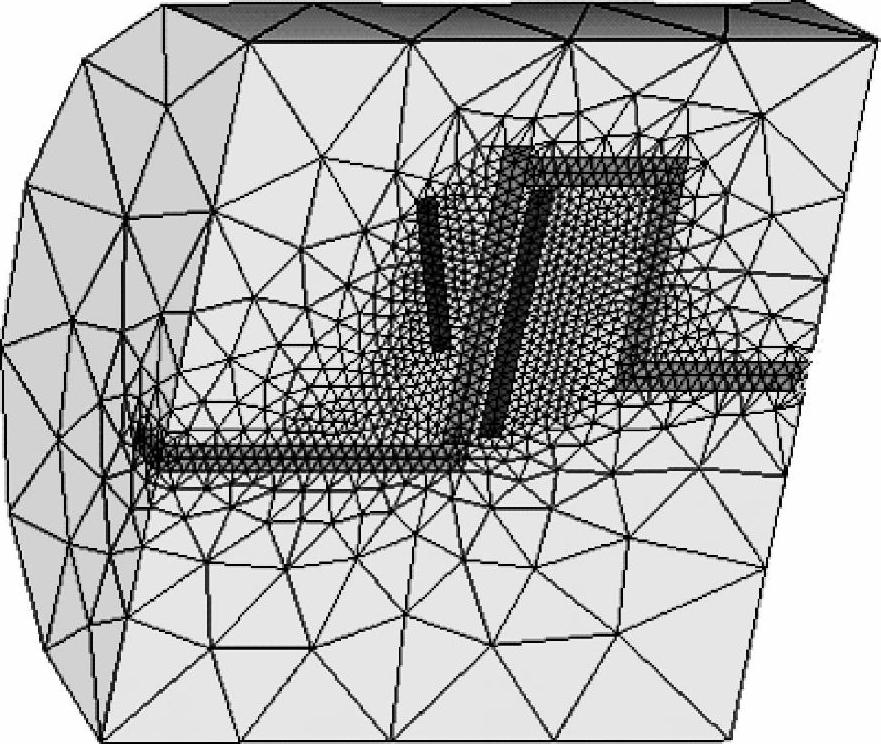
图6-5 磁脱扣器场域有限元剖分图

图6-6为仿真获得的磁脱扣器在不同电流下吸力矩随气隙（衔铁与轭铁夹角）的变化曲线。这些结果数据的列表也即为保护特性计算所需要的静特性数据网格。

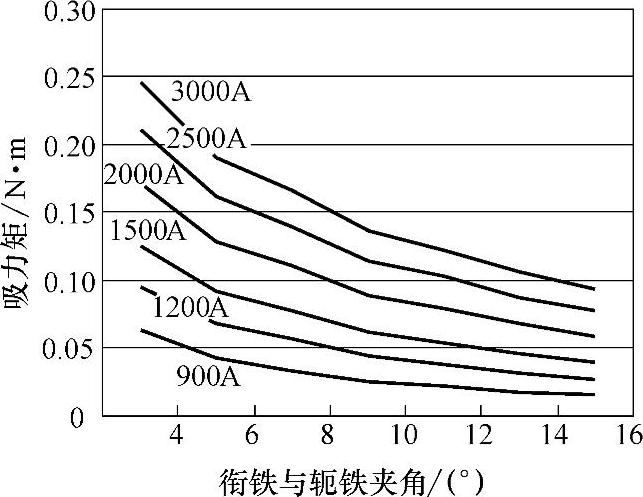
图6-6 不同电流下吸力矩随气隙变化曲线

3.脱扣器保护特性计算

结合静态特性计算得到的数据网格，磁脱扣器的动态特性，即保护特性，可以通过求解下面的方程组得到：

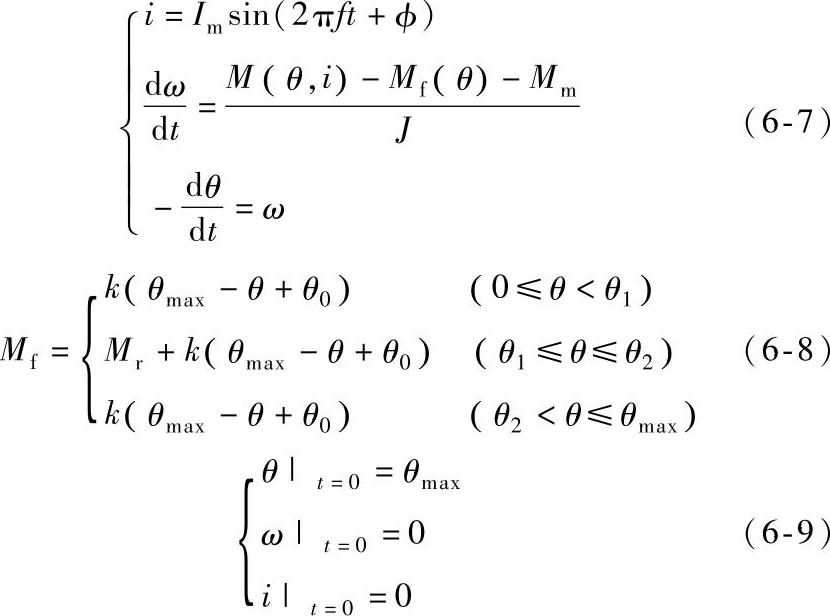
式中 θ——衔铁与轭铁夹角（工作气隙）；

i——激磁电流；

∅——短路合闸相角；

I_m——电流幅值；

J——动铁心转动惯量；

ω——动铁心角速度；(www.xing528.com)

M_m——摩擦力矩；

M——吸力矩；

M_f——反力矩；

k——反力弹簧平均弹性系数；

θ₀——反力弹簧初始拉伸（压缩）角度；

M_r——平均脱扣力矩。

M_f包括两部分：反力弹簧反力和脱扣力，其中脱扣力的作用行程很短，仅在θ₁≤θ≤θ₂时起作用，图6-7为反力示意图。

θ₂-θ₁＜＜θ_max-θ₂ （6-10）

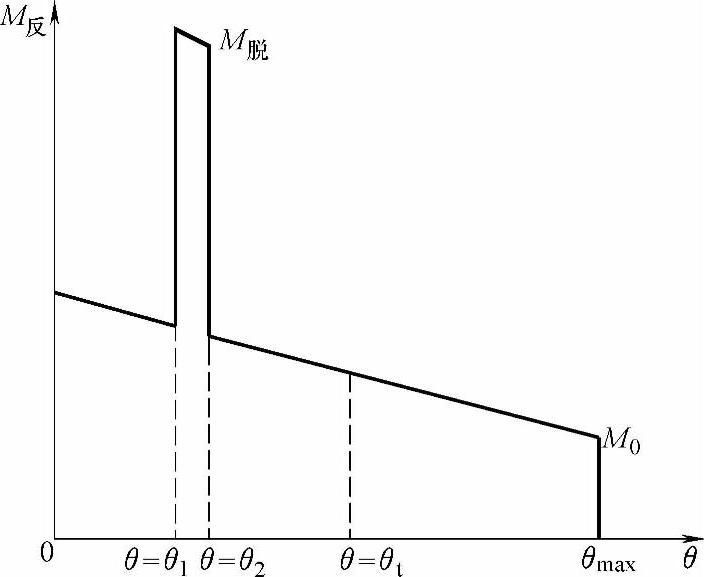
图6-7 磁脱扣器反力示意图

磁脱扣器在短路电流作用下的动作过程分为两个阶段，第一阶段为电磁铁触动过程，是从短路电流发生到衔铁开始动作，这一阶段衔铁不会动作，直到吸力矩大于反力矩，而θ=θ_max，计算中仅求解式（6-7）中的第一个方程（电路瞬态方程）；第二阶段为脱扣器衔铁运动过程，从衔铁开始运动到其带动脱扣杆并使机构脱扣为止，这一阶段的计算就是联立（6-7）中的三个方程用四阶龙格-库塔法进行离散求解，过程中所需吸力和磁链值仍由对静态数据网格二次插值得到。衔铁转动过程中的摩擦阻力主要在转轴处，力矩很小，计算中忽略不计。

表6-2示出了研究对象磁脱扣器动态特性计算的参数。

表6-2 磁脱扣器动态特性计算参数

图6-8示出了用上述方法仿真计算获得的电磁脱扣器在1500A短路电流下的动态特性曲线。

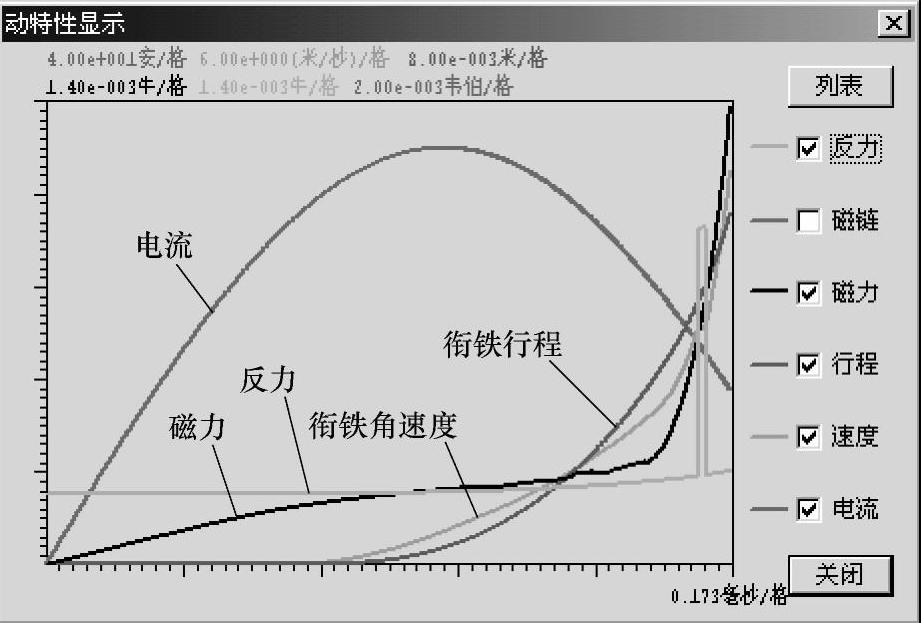
图6-8 1500A短路电流下电磁脱扣器动态特性曲线

脱扣器动作时间的测量原理如图6-9所示。

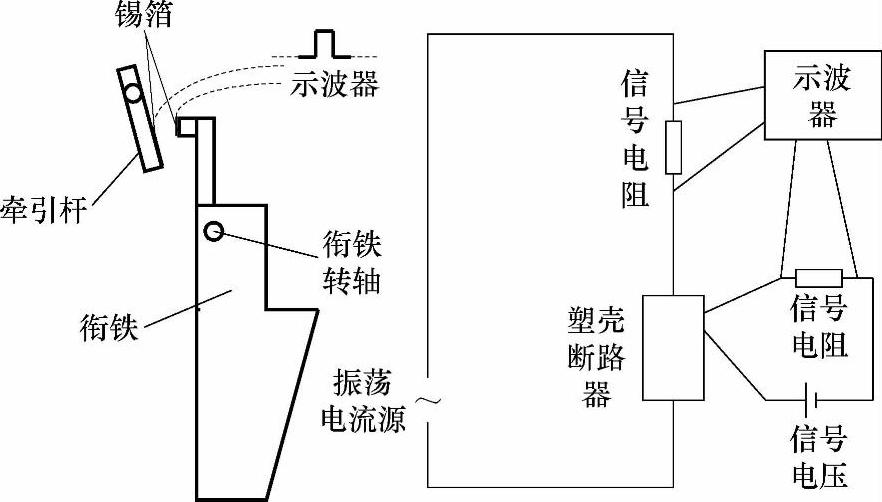
图6-9 脱扣器动作时间测量原理图

短路电流到来后，脱扣器吸力克服反力开始运动，当衔铁打到牵引杆上时，粘在上面的极薄的锡箔相接触，外部测量电路接通，示波器接收到一个电压上升沿信号，记录短路电流起始点到该上升沿信号之间的时间差作为测量值，但此时并未脱扣，衔铁还要转动一个角度才能带动牵引杆脱扣。实验中，测量值小于脱扣时间，衔铁转角为θ_max-θ_t，相应地与实验对比的计算值也取同样的行程（见图6-7），实验值与计算值的对比曲线见图6-10，表6-3为脱扣器动作时间计算值与实验值的对比。

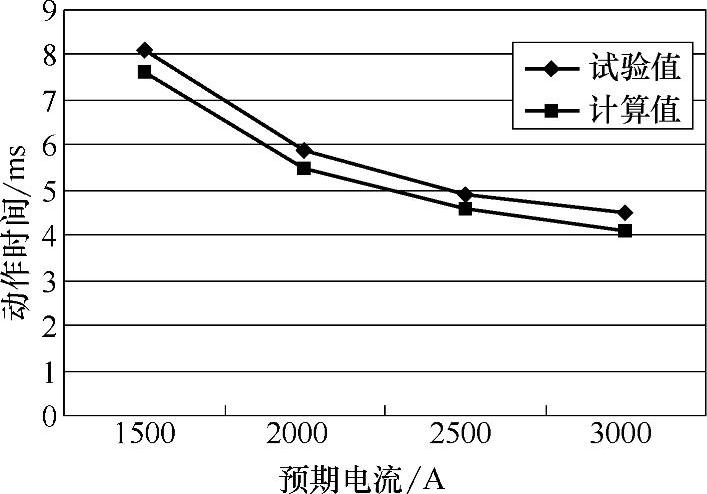
图6-10 脱扣器动作时间实验值与计算值对比

表6-3 脱扣器动作时间实验值与计算值对比

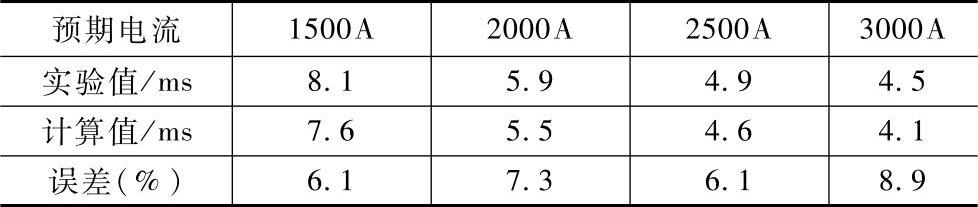
实验验证表明：计算值相对于试验值的误差不超过9%。

4.磁脱扣器保护特性分析

磁脱扣器的动态特性包括衔铁与轭铁转角θ=θ（t）、吸力矩M=M（t）、角速度ω=ω（t）、电流i=i（t）、反力矩M_f=M_f（t）、脱扣时间t_r、脱扣电流I_r，其中最主要的性能指标是t_r，在同样的短路电流下，t_r越小越有利于限流和开断。脱扣器在不同短路电流下的t_r构成保护特性，如图6-11所示为仿真获得的上述磁脱扣器（I_r=1500A）的保护特性曲线：

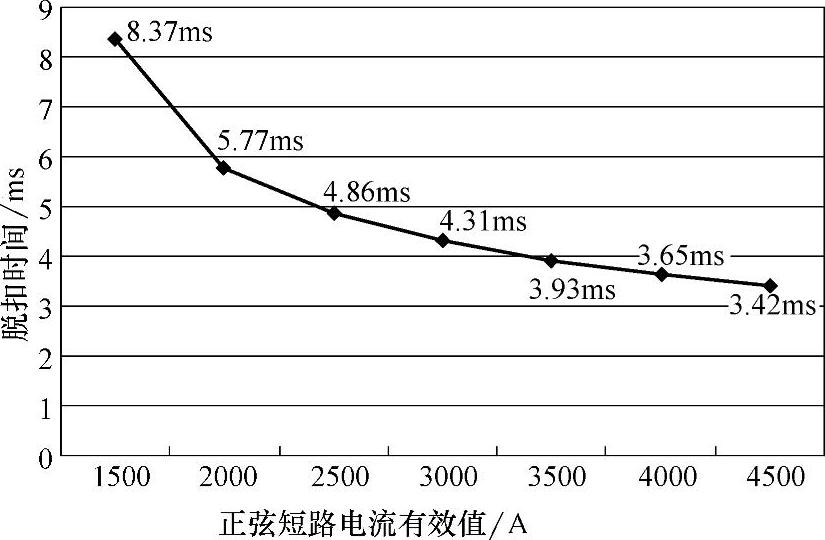
图6-11 磁脱扣器保护特性仿真曲线

从图6-11中可以看到，短路电流从临界值1500A到2000A这一区段内t_r随电流增大减小最快，达2.6ms；从2500A之后，t_r减小的速度明显变慢，从2500A到4500A，t_r仅减小1.44ms。

（1）保护特性与反力弹簧特性的关系。磁脱扣器的动作时间与动作值决定于电磁铁动态吸力特性与负载反力特性的配合，增大反力会提高动作时间和动作电流；减小反力会减小动作时间和动作电流。这样，在磁脱扣器的设计中，当磁系统确定后，就可根据需要选取反力特性，其值由脱扣器的动特性计算决定。

图6-12和图6-13分别示出了其他参数不变，仅改变弹簧刚度k和反力弹簧初始拉伸（压缩）角度θ₀时保护特性的变化曲线。

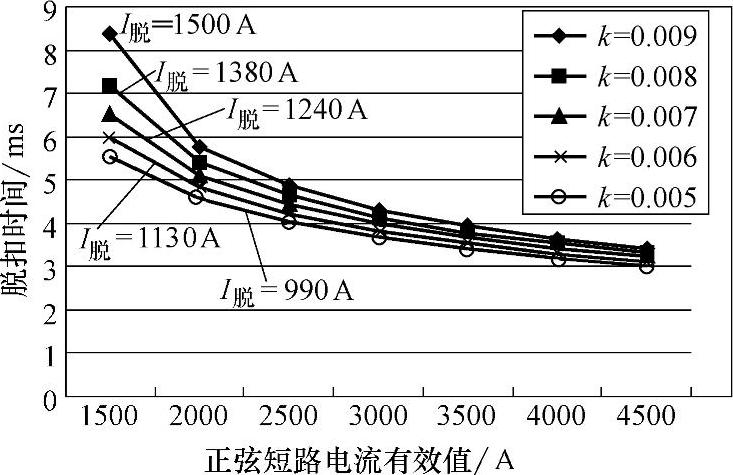
图6-12 磁脱扣器保护特性随k变化的曲线

图6-12和图6-13中可见，随着k和θ₀的减小，脱扣电流I_脱逐渐减小，相同电流下的脱扣时间也随之缩短，但随着电流的增大，缩短越来越慢，电流达到45I_e时脱扣时间最长与最短相差小于0.5ms。当k以等差数列减小时，I_脱的减小不为等差数列；而当θ₀以等差数列减小时，I_脱则呈等差数列减小，因此通过改变反力弹簧的初始长度更容易实现断路器脱扣电流的线性调节。

（2）保护特性与初始工作气隙的关系。从图6-6可以看到：衔铁所受磁力随气隙减小而增大，并且上升越来越快。改变初始气隙（脱扣时衔铁行程作同样变化），脱扣器的脱扣时间和脱扣电流也随之变化，表6-4列出了其他不变，改变衔铁初始工作气隙（转角）θ_max时，脱扣时间和脱扣电流的变化关系。

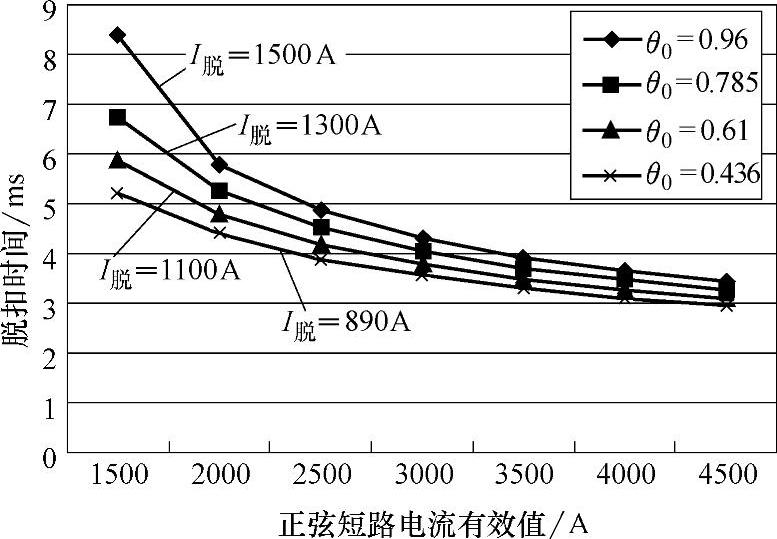
图6-13 磁脱扣器保护特性随θ₀变化的曲线

表6-4 脱扣电流和脱扣时间随θ_max的变化关系

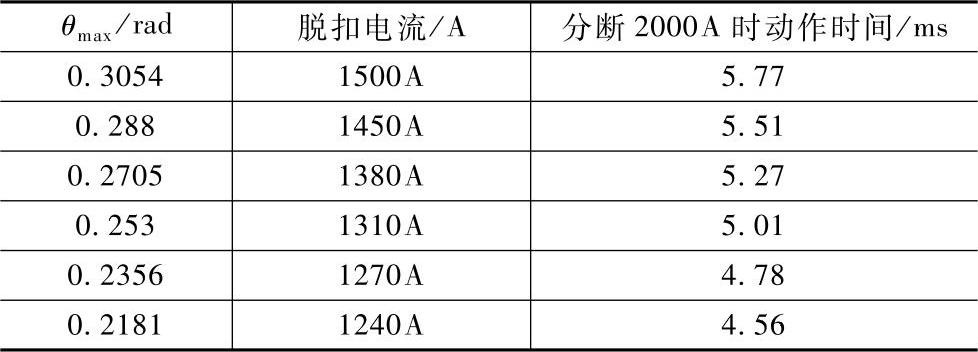
表6-4可见，减小θ_max时，脱扣电流和脱扣时间都随之减小。θ_max从0.3054弧度减小到0.2181弧度，幅度为28.6%，脱扣电流则从1500A减小到1240A，幅度为17.3%；由图3-11可见，θ₀从0.96弧度减小到0.436弧度，幅度为54.6%，脱扣电流则从1500A减小到890A，幅度为40.7%。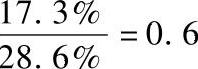小于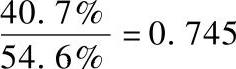，由此可见改变同样大小的脱扣电流，调节θ_max的方式所需的调节量比调节θ₀的方式更大，并且从表6-4中还可看到脱扣电流随θ₀的变化是非线性的。由以上分析结果可得出：当塑壳断路器磁脱扣器的磁系统尺寸确定时，可通过改变反力弹簧的刚度和初始拉伸（压缩）长度来适应不同额定电流和脱扣电流的要求。相对于弹簧刚度的调节方式，通过改变反力弹簧的初始拉伸（压缩）长度调节脱扣电流更易实现线性调节；其他条件不变时，改变磁脱扣器的初始工作气隙，脱扣电流随之做非线性变化；相对于改变反力弹簧初始拉伸（压缩）长度调节脱扣电流的方式，改变初始工作气隙对脱扣电流的调节范围较小。